arc100 F Colorful Sequences （计数）

题意

定义一个长度为n的，值域为 $[1,k]$的序列是colorful的，当且仅当他存在一个长度为k的子串是连续段。
现在给出一个长度为m的序列A，问在所有长度为n的colorful的序列中，A的总出现次数之和。

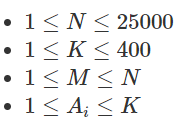
思路

• A在所有序列中的出现总数是 $(n-m+1)K^{n-m}$。
• 现在考虑计算A在所有non-colorful的序列中的出现次数。
• 若A是colorful的，则是0。否则有：
• 若A中存在相同元素，此时跨过A不存在K-连续段。因此只需要求出 $f[i]$表示左边接一个长度为i的序列，保证A与这个序列的拼接不存在K-连续段的方案数；右边同理，做一个卷积即可。
• 若A中的元素两两不同，A的具体内容是与答案无关的。
• 不好直接计算A在所有non-colorful的序列中的出现次数
• 考虑计算所有长度为n的non-colorful序列中，有多少长度为m的任意互异段。这通过一个dp也可以快速计算。最后除掉 $A_{k}^{m}$即可。

关于dp的方法：
上面使用的两个dp方法是类似的。

• 设状态 $F[i][j]$表示长度为i，目前有j个互异的在末尾（倒数第j+1个与这j个中的某个相同）的没有K-连续段的序列方案数。
• 决策时，注意到不需要知道前面确切的选取方案（这也是设这个状态的原因）。
• 放一个互异即转移到 $F[i+1][j+1]$，系数是 $K-j$
• 同时也可以转移到某个 $F[i+1][j'],1\leq j'\leq j$。
• 前缀和优化， $O(nk)$

此题的方向在于对A情况的讨论，再上一些计数技巧即可。

#include <bits/stdc++.h>
using namespace std;
const int N = 25000 + 10, K = 410, mo = 1e9 + 7;
typedef long long ll;
int n,k,m,a[N],cnt[K];
ll ans;
ll ksm(ll x, ll y) {
	ll ret = 1; for(; y; y>>=1){
		if (y & 1) ret = ret * x % mo;
		x = x * x % mo;
	}
	return ret;
}


ll f[2][K], o, g[2][K];
inline void add(ll &x, ll y) {
	x = (x + y) % mo;
}

//长为n的non-colorful的串中，长为m的互异连续段有多少个.
ll dp1() {
	memset(f[o], 0, sizeof f[o]);
	memset(g[o], 0, sizeof g[o]);
	g[o][0] = 1;
	for(int i = 0; i < n; i++) {
		memset(f[1 - o], 0, sizeof f[1 - o]);
		memset(g[1 - o], 0, sizeof g[1 - o]);
		for(int j = 0; j < k; j++) {
			if (j + 1 != k) {
				add(g[1 - o][j + 1], g[o][j] * (k - j));
				add(f[1 - o][j + 1], f[o][j] * (k - j));
				add(g[1 - o][j + 2], - g[o][j] * (k - j));
				add(f[1 - o][j + 2], - f[o][j] * (k - j));
			}
			add(f[1 - o][1], f[o][j]);
			add(f[1 - o][j + 1], - f[o][j]);

			add(g[1 - o][1], g[o][j]);
			add(g[1 - o][j + 1], - g[o][j]);
		}
		o = 1 - o;
		for(int j = 1; j < k; j++) {
			add(g[o][j], g[o][j - 1]);
			add(f[o][j], f[o][j - 1]);
		}
		for(int j = m; j < k; j++)
				add(f[o][j], g[o][j]);
	}
	ll ret = 0;
	for(int i = 0; i < k; i++) add(ret, f[o][i]);
	return ret;
}

ll le[N][K], ri[N][K];
void dp2(int sig, ll f[N][K]) {
	memset(f, 0, sizeof f);
	memset(cnt, 0, sizeof cnt);
	if (sig == 0) { //left
		for(int i = 1; i <= m; i++) if (cnt[a[i]] == 0) {
			cnt[a[i]]++;
		} else {
			f[0][0] = f[0][i - 1] = 1;
			break;
		}
	} else {
		for(int i = m; i; i--) if (cnt[a[i]] == 0) {
			cnt[a[i]]++;
		} else {
			f[0][0] = f[0][m - i] = 1;
			break;
		}
	}
	for(int i = 0; i < n - m; i++) {
		for(int j = 1; j < k; j++) {
			if (j + 1 != k) {
				add(f[i + 1][j + 1], f[i][j] * (k - j));
				add(f[i + 1][j + 2], - f[i][j] * (k - j));
			}
			add(f[i + 1][1], f[i][j]);
			add(f[i + 1][j + 1], - f[i][j]);
		}
		for(int j = 1; j < k; j++) {
			add(f[i + 1][j], f[i + 1][j - 1]);
			add(f[i + 1][0], f[i + 1][j]);
		}
	}
}

int main() {
	freopen("f.in", "r", stdin);
	cin>>n>>k>>m;
	for(int i = 1; i <= m; i++) scanf("%d", &a[i]);
	ans = (n - m + 1) * ksm(k, n - m) % mo;

	int non = 0;
	if (m >= k) {
		int js = 0;
		for(int i = 1; i <= k; i++)	{
			if (cnt[a[i]]++==0) js++;
		}
		if (js != k) {
			for(int i = 1; i + k - 1 < m; i++) {
				if (--cnt[a[i]]==0) js--;
				if (cnt[a[i + k]]++==0) js++;
				if (js == k) break;
			}
		}
		non = js != k;
	} else non = 1;

	if (non) {
		int same = 0;
		if (m <= k) {
			for(int i = 1; i <= m; i++) {
				for (int j = i + 1; j <= m; j++) if (a[i] == a[j]) {
					same = 1; break;
				}
			}
		} else same = 1;
		if (!same) {
			ll P = 1;
			for(int i = k; i > k - m; i--) P = P * i % mo;
			ans = (ans - ksm(P, mo - 2) * dp1()) % mo;
		} else {
			dp2(0, le), dp2(1, ri);
			for(int i = 0; i + m <= n; i++) {
				ans = (ans - le[i][0] * ri[n - m - i][0]) % mo;
			}
		}
	}
	cout << (ans + mo) % mo<<endl;
}