失效的欧拉方程
这是一篇来自公众号“原理”的文章,我对其作了一些注释、推导与思考,相应的,可能会有一篇或一系列总结类或者拓展类的文章陆续上传。
这篇博客的目的是介绍一些文章中涉及的物理与数学概念,使我们能对文章内容有一个大致把握,同时做一些关于相关问题的讨论和一些概念的简单推导,加深我们对文章内涵的理解。
文章中灰色背景的引用文字为原文章内容,其它文字和公式是我的一些简单解释、讨论或推导。
总体内容:我们将比较全面的讨论相关物理与数学概念,推导欧拉方程,见识理想流体在欧拉方程的约束下产生的某些奇怪的性质(那些点就叫“奇点”,而在讨论黑洞时,“奇点”通常指的是那些密度无限大的点,一切物理定律在那里都将崩溃,这是《时间简史》告诉我的)。
文章中的数学仅仅限于:
(1).用数学定义式帮助我们更好的理解物理概念。
(2).在推导欧拉方程中涉及一些高等数学,但这是必要的。
我们可能不会或很少会用数学方面的讨论来解释欧拉方程的失效性,因为就像文章所说,数学家们长久以来都在找这些“奇点”,这应该大大超出了我的数学能力,而我同样也没有大把的时间可以用于掌握新的数学。
第一部分:理想世界的流体方程
—— 关于理想流体与欧拉方程及其简单推导
1757年,数学家欧拉(Leonhard Euler)发现了后来被称为“欧拉方程”的流体方程,这些方程描述了流体随时间的演化,就像牛顿的力学方程描述台球在桌子上的运动一样。
- 理想流体:既然欧拉方程是研究流体的理想方程,那么其研究的流体也是一种经过抽象的理想模型。当流体不计粘性时,我们就把它叫做理想流体。对于实际的、具有粘性的流体,在运动状态下两个紧挨的层之间会由于速度不同而产生一对拖动力与阻力,从而在流体内部(或者说层与层之间)将产生内摩擦力(粘滞力),造成机械能的损失与热量的产生,而且这一能量转化过程是不可逆的。所以,内摩檫力是流体运动时机械能损失的根源。这种内摩檫力较为复杂,所以在分析某些实际问题时我们使用用理想流体模型进行处理是一种利于抓住问题主要矛盾的做法。
欧拉方程是一种理想化的对流体运动的数学描述,它们在一定的假设范围内,模拟流体的运动。更确切地说,欧拉方程描述了流体中无穷小的粒子的瞬时运动。这个描述包括一个粒子的速度和它的涡量(即旋转的速度和方向)。总的来说,这些信息汇聚成了一个“速度场”,描绘了流体在给定时刻的运动情况。欧拉方程从一个初始速度场开始,预测它在未来每一刻会发生的变化。
- 场:物理学家用场表示某一物理量在空间中的分布。我们可以通过一个空间位置函数使这个物理量在空间中的分布具有很好的数学形式(空间位置与相应物理量之间的一个映射)。例如,标量场中空间的每一点都对应该物理量一个确定数值大小,而矢量场每一点则对应该物理量的数值大小与方向。虽然场被定义成空间中的数,但场在物理意义上是具有真实性的。例如一些守恒的物理量在两个粒子之间的传递若不是瞬间完成的(超距作用),那么在传递过程中这个量就是存在于场中的,否则这个守恒量就不守恒了。实际上,实物和场都是物质存在的基本形态。
两个多世纪以来,它们似乎做到了描述任何情况下的任何流体运动。然而多年来,一些数学家一直怀疑欧拉方程在某些特定的情况下会失效,因为欧拉方程并不是对真实世界流体的完全描述,它包括几个非物理性的假设。例如,它们假设当流体的内流在流过彼此时,不会产生摩擦;再比如它们还假设流体是“不可压缩的”,这意味着在欧拉方程的世界里,流体是无法被压缩到比它已经占据的空间更小的空间里的。
- 原文中欧拉方程的形式:

(其中u为流体的速度场,p为内压强)- 梯度:函数在该点的方向导数沿梯度方向取得最大值。具体计算公式为
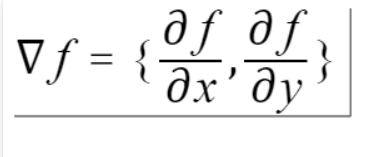
- 散度:表示某点处单位体积内散发处的矢量F的通量,描述了通量源的密度。这一点我们可以从公式中看出:

- 梯度:函数在该点的方向导数沿梯度方向取得最大值。具体计算公式为
- 欧拉方程的推导:实际上欧拉方程有其它不同数学形式的表达,下面我们尝试进行推导。
(最后你会发现我们将上面那组方程中的第一个方程直接推导了出来,而第二个方程实际上指的是理想流体的不可压缩性导致其体膨胀为0。所以实际上我们将欧拉方程完整推导了出来。)- 流体微元的受力:当我们将流体微元所受重力忽略时,其所受合力为各面压强之和,公式为
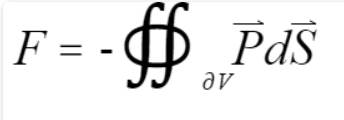
其中,向量f大小为面积元大小,方向为沿流体元表面法线方向向外。利用高斯公式,我们将其转化为对体的积分,公式变为
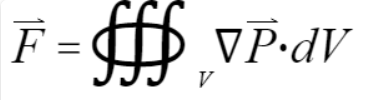
- 利用牛顿第二定律:我们计算出流体微元的加速度,并同时消去积分符号与体积,可以得到方程
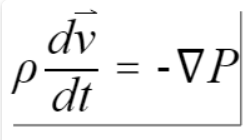
- 利用随体导数公式:将上一步所得方程左边进一步打开,并且将流体微元所受重力考虑进去,可以得到方程
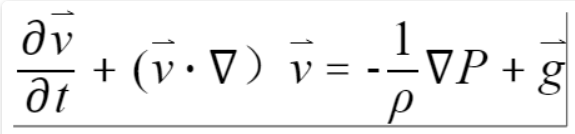
这就是我们对理想流体应用牛顿第二定律推导出的欧拉方程。
- 流体微元的受力:当我们将流体微元所受重力忽略时,其所受合力为各面压强之和,公式为
- 补充内容:
- 随体导数:表示流体质点在欧拉场内运动时所具有的物理量对时间的导数。例如当我们取流体质点的速度矢量v(r,t),其中r为质点位矢时,根据复合函数微分法则,可得
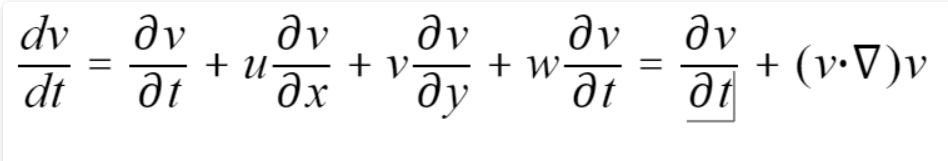
其中u、v、w为速度在直角坐标系中的三个分量,我们称随体导数等于局部导数(当地导数)和位变导数(对流导数)之和。 - 高斯公式:
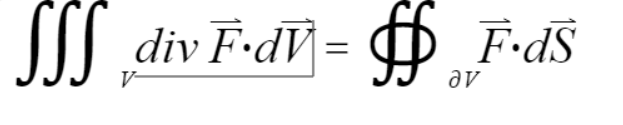
(其中 ∂V表示空间有界区域的分片光滑闭曲面。)
- 随体导数:表示流体质点在欧拉场内运动时所具有的物理量对时间的导数。例如当我们取流体质点的速度矢量v(r,t),其中r为质点位矢时,根据复合函数微分法则,可得
显然,真正的流体内部是有摩擦的,欧拉方程的描述将流体的运动规定在了一个特定的理想化世界中。若要模拟更真实的流体运动,则需要使用纳维-斯托克斯方程(NS方程)。许多数学家和其他研究人员想要知道,在科学上仍占有非常崇高地位的欧拉方程,在无摩擦、不可压缩的理想化世界中,是否总是能够精确地描述流体的所有未来运动状态。
- 纳斯-斯托克斯方程(Navier-Stokes equations):描述不可压缩(流体密度固定)、粘性系数为一常数的流体动量守恒的运动方程。具体方程为
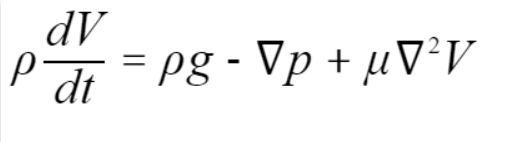
其中常数u是动力粘性系数,你会发现这与我们推导的公式十分接近。- 动力粘性系数:表征液体粘性的内摩擦系数,定义为应力(物体发生形变时内部各部分之间产生的相互作用的内力)与应变速率(单位时间内单位长度线元的变化量)之比。动力粘性系数(及粘度或动力粘度)是流体的一种属性,对于同种流体,粘度与温度有显著关系而与压强几乎无关。
终于,一个新的证明找到了会让欧拉方程失效的特定条件。
第二部分:欧拉方程的缺陷
——让欧拉方程失效的致命无穷大
今年,加利福尼亚大学圣迭戈分校(UCSD)的数学家Tarek Elgindi分别于4月和10月向arXiv提交了两篇论文,这两篇论文推翻了这组著名流体方程在几个世纪以来的假设。
Elgindi证明了,在一组特定的情况下,欧拉方程会开始输出无意义的东西。他所找到的特例令众数学家们大吃一惊,因为这一“特例”是过去数学家们一直以为总能使方程有效的条件。但这并不代表欧拉方程从此将失去它在科学界的重要地位。
让我们回顾一下我们的欧拉方程推导过程:实际上,我们只是简单的考虑了流体微元之间的压强和流体微元所受的重力,并没有考虑流体内部的粘滞力。从能量的角度看,我们的理想流体模型 并没有能量的损失。
从理论上说,根据欧拉方程的运作原理,当你将当前状态的值代入方程中之后,就能产生未来某一时刻的精确值;再将未来某一时刻的值代入方程,就能再次延伸预测。通常情况下,这个过程是一直有效的,它似乎能延伸到我们可预见的遥远未来。但是,一旦在这个过程中欧拉方程开始产生一个无法继续代入计算的值时,欧拉方程便失效了。
是什么样的值无法被继续代入计算?它们一定是以某种非常不合理的方式放大了流体中的某个点的速度或涡量。这种放大非常极端,会将某一点的速度或涡量在有限的时间内放大到无穷大。一旦出现无穷大,方程就会崩溃,无法再继续对未来状态进行描述。
注意:这种传导是我们假设欧拉方程成立的情况下对我们的理想模型讨论的结果。如果出现某种不合理的放大,那么这种放大可以是欧拉方程在运算中导致的,这种情况告诉我们,对于我们用理想模型的限制的流体,欧拉方程并不是处处适用的;另一种想法是,如果如果我们承认欧拉方程是正确的,那么这种不合理的放大则是我们的流体导致的,我们的流体出了问题:在某些情况下它的一些流体微元拥有实际上无穷大的速度!显然,前者比后者更容易让我们接受。
这就是欧拉方程失效的原因。
(我们忽略了理论上更加结实的数学推导过程,因为它超出了我的知识和时间能力。)
- 涡量:流体速度矢量的旋度。在流体中,若存在涡量源(即速度场不是无源场),则将产生尺度大小不一的涡旋,而涡旋的强度与方向则使用涡量来表示。
- 旋度:表示三维向量场对某一点附近的微元造成的旋转程度(也就是向量场在某点的旋转性质)的一个向量。下面我们来具体看看旋度是如何计算的:
- 环量的计算:给定三维空间中的向量场(或者说函数v = f(x,y,z)), 则此向量场沿着某简单有向闭曲线L的环量的计算公式为
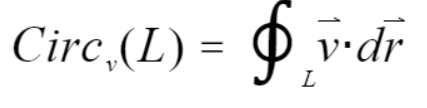
当向量场中某一区域的环量不为0时,说明向量场在这个区域中表现出环绕某一点或某一区域旋转的特性。 - 旋度的计算:旋度是用来表示某一点附近向量场旋转程度的,我们需要用到环量的极限,即
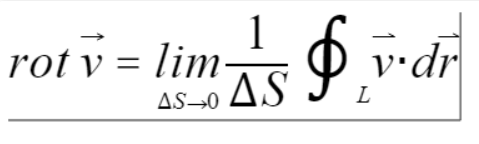
可以看出,旋度同密度、温度一样,是向量场的一种强度性质。当向量场旋度并非处处为零时,我们称其为有源场,否则称之为无源场。
- 环量的计算:给定三维空间中的向量场(或者说函数v = f(x,y,z)), 则此向量场沿着某简单有向闭曲线L的环量的计算公式为
- 旋度:表示三维向量场对某一点附近的微元造成的旋转程度(也就是向量场在某点的旋转性质)的一个向量。下面我们来具体看看旋度是如何计算的:
- 为什么我们要引入涡量:对于流体,其在受到力的作用时,由于流体不能承受切应力,每个流体微元都有其自己的状态。通过涡量的引入,我们可以很好的描述这种现象。这也是流体与刚体的不同之处。
- 切应力:前面我们在动力粘性系数中简单讨论过应变力。在流体中,我们讨论的应变力通常为切应力。我们将液体流动时的流向看作是一个平置的圆柱,则液体中相对移动的各层之间产生的内摩檫力一半沿着这个圆柱横截面的切线方向,我们将其称为切变力(或者剪切力)。单位面积上的切变力被称为切应力。切应力是导致流动发生形变的原因。
这些致命的极值被称为“奇点”。因此当数学家在询问“欧拉方程是否总是成立”时,他们实际上是在问:欧拉方程是否会在某些情况下产生奇点?
(奇点的奇异性质是流体在受到有限的应变力时,某些流体微元将拥有无穷大的速度大小)
多数数学家相信答案是肯定的,但他们从来没有找到一个具体的实例。直到Elgindi的证明出现。他的结果虽然没有表明欧拉方程会在某个确切条件下产生奇点,但这已经是迄今为止最接近这一目标的结果。
第三部分:问题的突破
——找到“奇点”的方法
为了实现这个目标,Elgindi考虑了一个简化版的流体运动模型。在真实的三维流体中,任何粒子都有三个可以移动的轴,即x轴(左右)、y轴(上下)和z轴(前后),它们有很大的运动自由度;而且流体中的不同部分的粒子的运动不一定有任何密切联系。
在Elgindi的研究中,他简化了欧拉方程需要处理的工作。他让流体的运动关于z轴对称,这种对称在真实流体中虽然并不存在,但却能使得对速度场的计算更加容易。他还限制了流体的运动范围,流体中的粒子只可以沿z轴的方向,或朝着或远离z轴运动,不能绕着z轴旋转。这样的设定基本上把问题简化成一个二维问题。
我们可以想像这些流体微元:它们不能绕着z轴旋转,但它们可以把自己“套”在x轴或者y轴上旋转,同时,如果这里有一个微元在按照规定的方式运动着,那么对称于z轴的另一个位置上有一个微元也在按照类似的方式的运动——唯一的区别是这两种运动的形式也应该关于z轴对称。
最后,Elgindi对他输入欧拉方程中的初始数据设定了一些额外规定。从某种意义上说,这些数据比描述真实世界流体的数值更加粗糙,更有可能形成奇点。
在现实世界里,如果你从流体中的一个点移动非常小的距离到另一点,那么第二个点的速度和第一个点的速度应该非常相似,它们的涡量应该也非常相似。具有这种特性的速度场被称为是“平滑”的,也就是说,当你从一个点移动到下一个点时,速度场的值会连续平滑地变化,而不是快速变化。
实际上这种平滑性也保证了在有限体积的流体中“奇点”无法出现。
但在Elgindi对流体的描述中情况却不是这样,他的数据中的涡量变化更大。虽然看起来Elgindi的简化似乎与现实的流体行为偏离太多,但与许多其他数学家为研究欧拉公式所做过的简化相比,这已经是非常温和的设定。最终,Elgindi证明了在这些简化过的情况下,欧拉方程已经开始产生非常意外的结果。
这时我们已经找到了一些能使“奇点”出现的条件,,比如上边讲述的特殊的运动形式以及某些特殊的初始状态。
在Elgindi的证明中,他设定的流体是没有边界的,就像是在空间漂浮的一个点。现在,我们用水箱中的水为例来理解他的证明。想象在水箱的两端有两个厚厚的水环,它们就像漩涡一样在流体的主体内形成有组织的扰动。这种现象在自然界中确实存在。
现在,假设这两个环朝着相对的方向移动。在前进的过程中,欧拉方程正常运行,计算出流体在每个时刻的速度场。但当环越靠越近时,方程就开始出现一些异常值。方程计算出的结果显示**,当两个环越靠越近时,它们就以越来越大的强度相互吸引,导致环的中央被拉长了,看起来更像一对漏斗。随着它们的中心越靠越近,它们的速度也越来越快,最终相撞**。
观察相撞时的速度场,就能看到从未在欧拉方程的假设情况下所看到的东西——奇点。Elgindi证明了欧拉方程在相撞的点能计算出无穷大的涡量。
让我们将所作的讨论与数学家通过他的数学方法证明的情况进行对比:
(1).特殊的初始状态:流体内有两个水环在对流体进行扰动。
(2).对称的运动形式:扰动流体运动的两个水环在做关于z轴对称的运动,这两个有力的水环导致的流体运动也应该关于z轴对称。
(3).没有边界的流体:流体的平滑性导致“奇点”只可能存在于无限大的流体中。
Elgindi的结果完全改变了数学家看待欧拉方程的方式。在此之前,数学家从来没有证明过,在没有边界的情况下,欧拉方程只在短时间内有效,而不是永远有效。在这场漫长的寻找欧拉方程中的“弱点”的拉锯战中,终于有一位数学家作出了突破。
我们或许可以通过对MATLAB的学习来对这种特殊情况进行建模,这绝对是很有趣的。但经过这些讨论,我们也应该看到,即使在某些异常的情况下欧拉方程会出现“奇点”,但它的价值依然不可忽视——我们是在工程上讨论这些问题,而非在哲学上讨论,这也就是说,我们不需要完美的定律。一个近似的定律往往具有同样大的作用。但是,就像《费曼物理学讲义》中费曼告诉我们的,“纵然质量的变化只是一点点,我们的整个世间图景也得改变”——欧拉定律的失效带给我们的价值,或许正是这种观念上的变化。
