1、线性规划的一般形式
min(max) c1x1+c2x2+···+cnxn
s.t. a11x1+a12x2+···+a1nxn≥(或≤,=)b1
a21x1+a22x2+···+a2nxn(或≤,=)b2
··· ···
am1x1+am2x2+···+amnxn(或≤,=)bm
x1,x2,···,xn≥0
2、线性规划的标准型
min c1x1+c2x2+···+cnxn
s.t. a11x1+a12x2+···+a1nxn=b1
a21x1+a22x2+···+a2nxn=b2
··· ···
am1x1+am2x2+···+amnxn=bm
x1,x2,···,xn≥0
其中bi ≥0.
可以看到,只要将一般形式的大于号或者小于号全部去掉,用等号代替,就可以得到线性规划的标准型
3、矩阵-向量形式的标准型
min cTx
(LP) s.t. Ax=b
x≥0
其中
c=(c1,c2,···,cn)T,x=(x1,x2,···,xn)T,b=(b1,b2,···,bm)T

其中,c:是价格向量,A是约束矩阵,b:是右端向量
记A=(p1,p2,··· ,pn),其中pj=(a1j,a2j,···,amj)T,线性规划(LP)又可以表示为
min cT x
(LP) s.t. Σxj*pj=b 从j=1到n求和
xj≥0,j=1,2,...,n
4、线性规划解的情况
满足约束条件的向量x是可行解,全体可行解构成可行域D.
D= Φ 时,称线性规划无可行解;
D≠ Φ 时但目标函数无下界时,称线性规划(LP)无界或无最优解;
D≠ Φ 时若目标函数有下界,可以证明线性规划(LP)必有最优解.
5、可行域为凸集
线性规划问题
min cTx
(LP) s.t. Ax=b
x≥0
的可行域D为凸集.
证明 任取x,y ∈ D,则有
Ax=b,x≥0, Ay=b,y≥0
对任意的α ∈ [0,1],设
z=αx+(1-α)y,则z≥0,且
Az=A(αx+(1-α)y)
=αAx+(1-α)Ay
=αb+(1-α)b
=b
因此z ∈ D
D为凸集.
6、线性规划一般形式转化为标准型
即如何将我们的线性规划的大于号小于号去掉
首先,将极大转换为极小,如求最大的f(x)相当于求最小的-f(x)
max f(x) → min –f(x)
然后,根据下面的公式
Σaij*xj≤bi
令xn+i=bi-Σaij*xj
则有xn+i≥0,Σaij*xj+xn+i=bi
最后,将自由变量xj转化,引入非负变量xj’和xj’’
xj’≥0,xj’’≥0
令xj=xj’-xj”
**举例:**我们想要将如下线性规划转化为标准型
min y=2x1-x2-3x3
s.t. x1+x2+x3≤7
x1-x2+x3≥2
-3x1-x2+2x3=5
x1,x2≥0,x3是自由变量
证明:
令 x4=7-(x1+x2+x3),
x5=(x1-x2+x3)-2,
再令
x3=x3’-x3’’,
得到标准型
min y=2x1-x2-3x3’+3x3’’
s.t. x1+x2+x3’-x3’’+x4=7
x1-x2+x3’-x3’’-x5=2
-3x1-x2+2x3’-2x3’’=5
x1,x2,x3’,x3’’,x4,x5≥0
我们可以看到,首先,对于我们的条件不等式,我们可以将他全部转化为:
表达式≥0
的形式,然后用一个新的变量来代替表达式,如x4=表达式
然后,对于我们的自由变量,将其转化为两个正数的差值
最终,我们就可以得到我们的标准型线性规划。
这是重点,复习的时候需要认真看一下,不难,能看懂,相信自己,奥利给
7、线性规划基本概念
设约束矩阵A的秩为m (行满秩),且m≤n,则A中必存在m阶非奇异子阵B,不妨设
B=(p1,p2,···,pm)
称B为线性规划问题(LP)的一个基矩阵,或称为基,基矩阵中的列向量称为基向量,对应的变量称为基变量,其余变量称为非基变量。
8、基解
在约束方程组取定基矩阵
B=(p1,p2,···,pm)
之后,令非基变量均为0,得到的方程组
p1x1+p2x2+···+pmxm=b
有唯一解,这样得到约束方程组的一个解向量
x=(x1,x2,··· xm)T
通过这种方法得到的满足约束方程组的解称为基矩阵B对应的基解。
线性规划 (LP)的基解个数不会超过n关于m的组合
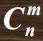
如果基解又满足非负条件,则称之为基可行解,此时的基B称为可行基
基可行解中非零分量的个数不会超过m,
若基可行解中非零分量的个数恰为m,称此基可行解为非退化的基可行解,否则称为退化的基可行解.
若一个线性规划的所有基可行解都是非退化的,称此线性规划是非退化的
简单地将,就是我们从我们的约束矩阵A中找到了一个基矩阵,通过这个基矩阵,我们可以将我们原本的表达式中的部分x变量变为0,然后得到一个新的表达式,这个表达式就是我们约束方程的一个解向量,这个解向量的解就是基解。而针对这个基解,如果基解大于0,就是一个可行解,如果这个可行解中的x的个数正好为x的总数m,说明没有一个x变量变为0,这个可行解就是不可退化的,也就是我们能够用的可行解。
举个例子:考虑线性规划
min 2x1-x2
s.t. x1+x2+x3 =5
-x1-x2 +x4 =0
2x1+2x2+x5=22
x1,x2,x3,x4,x5≥0
我们求一下这个线性规划最多有多少个基解,并求出所有的基解,极其对应的基,并判断是否可以退化。
证明:
首先呢,我们知道这是一个标准型线性规划,
也就是说我们不需要再进行转化了,而我们可以
看到,总共有x1..x5五个变量,所以n为5,而我
们却只有3个约束条件,说明m为3,取组合我们
可以计算出来,最多只有10个基解
实际上,由于我们要求的是与x1和x2有关的表达
式的最小值,也就是说x1与x2是线性相关的,也
就是说我们可以不考虑x1与x2同时出现的情况。
我们先列出所有的基可行解:
(p1,p2,p3)可舍去
(p1,p2,p4)可舍去
(p1,p2,p5)可舍去
(p1,p3,p4)
(p1,p3,p5)
(p1,p4,p5)
(p2,p3,p4)
(p2,p3,p5)
(p2,p4,p5)
(p3,p4,p5)
由此我们可以看到,实际上只用考虑7个基解
我们将这7个基解的对应的解求出来
比方说对(p1,p3,p4),我们就将上述三个条件中的p2与p5置零
我们可以得到如下的方程组
x1+0+x3=5
-x1-0+x4=0
2*x1+2*0+0=22
我们可以解得x1=11,x3=-6,x4=11
所以其对应的解向量就是(11,0,-6,11,0)
由于基解中有负值,所以不可行
同理,我们计算所有的基解的解向量,最终得到如下结果:
(p1,p3,p4),(11,0,-6,11,0)T不可行
(p1,p3,p5),(0,0,5,0,22)T退化
(p1,p4,p5),(5,0,0,5,12)T非退化
(p2,p3,p4),(0,11,-6,11,0)T不可行
(p2,p3,p5),(0,0,5,0,22)T退化
(p2,p4,p5),(0,5,0,5,12)T非退化
(p3,p4,p5),(0,0,5,0,22)T退化
如果觉得太麻烦,我们就用一个代码来解决好啦
import numpy as np
from numpy.linalg import solve
import itertools as it
import copy
if __name__=="__main__":
n=int(input('请输入有多少个变量'))
m=int(input('请输入有多少个表达式'))
print('请输入约束矩阵A')
A=[]
B=[]
for i in range(m):
A.append([])
a=input().split()
# A[i].append(a)
for j in range(n):
A[i].append(int(a[j]))
# print(A)
a=input('请输入常系数\n').split()
# B.append(a)
for i in range(m):
B.append(int(a[i]))
numa=1
numb=1
for i in range(m):
numa=numa*(n-i)
numb=numb*(i+1)
num=int(numa/numb)
print('基解一共有'+str(num)+'个')
X=[]
C=[]
for j in range(n):
X.append(j)
s=0
# for i in range(num):
for p in it.combinations(X,m):
C.append([])
for j in range(n):
C[s].append(0)
for j in range(m):
C[s][int(p[j])]=1
s+=1
# C.append(list(p))
# print(C)
# input()
o=0
for i in range(num):
o+=1
flagtuihua=1
flagkexing=1
q=0
# print(C[i])
A0=copy.deepcopy(A)#深拷贝
B0=copy.deepcopy(B)
for j in range(m):
for s in range(n):
if C[i][n-s-1]==0:
del A0[j][n-s-1]
# print(A0)
# print(B0)
a=np.mat(A0)
b=np.mat(B0).T
try:
result=solve(a,b)
except:
print('基解'+str(o)+':( ',end='')
for p in range(n):
if C[i][p]==1:
print('x'+str(p+1),end='')
q+=1
if q!=m:
print(' , ',end='')
print(' ) 无解')
else:
print('基解'+str(o)+':( ',end='')
for p in range(n):
if C[i][p]==1:
print('x'+str(p+1),end='')
q+=1
if q!=m:
print(' , ',end='')
print(' ),( ',end='')
q=0
w=0
for p in range(n):
if C[i][p]==1:
print(float(result[q]),end='')
if float(result[q])<0:
flagkexing=0
if float(result[q])==0:
flagtuihua=0
q+=1
else:
print('0.0',end='')
if w!=n-1:
print(' , ',end='')
w+=1
print(' ) ',end='')
if flagkexing==0:
print('不可行')
elif flagtuihua==0:
print('退化')
else:
print('非退化')
# input()
# a=np.mat(A)
# b=np.mat(B).T
# re=solve(a,b)
# print(re)
# print(A)
# for i in range(m):
# for j in range(n):
# print(A[i][j],end=' ')
# print()
今天下午刚刚写完的,大家看看好啦,个人理解个人理解

