高级数据结构之B树（B-tree）

一、B树（B-tree）的定义

B树是二叉树的一种推广，它在以硬盘为主的多级存储结构中常常被用来执行高效搜索。下图是一棵B树的简单示例，其中存储的是英语中的辅音字母。如果B树的一个内部结点x包含有x.n个关键字，那么它就会有x.n+1个孩子。结点x中的关键字是有序排列的，而且这些有序的关键字也把以x为根的子树中所包含关键字分隔成x.n+1个子域，每个子域对应一棵子树。当在一棵B树中查找一个关键字时，基于对存储在x中的x.n个关键字之比较，查找算法会从x.n+1个路径中做出选择。例如，要在下图中查找字母R，所有检查过的结点所构成的路径就被用浅影表示了出来。

B树（B-tree）是一种特殊的多路查找树，该树T需要满足如下一些条件：

1. 每个结点x有下面属性：

a）x.n，当前结点中存储有n个关键字；
b） $key_i$ 表示 $n$ 个关键字，其中 $i=1,2,\cdots,n$ ，关键字按非降序排列，即 $x.key_1\leq x.key_2\leq \cdots \leq x.key_n$ 。
c）布尔值 x.leaf 用以表示x是否为叶子结点，如果是叶子结点则其值为True，否则就为False。

2. 每个内部结点x还包含有x.n+1个指向其孩子的指针， $x.p_1, x.p_2, \cdots, x.p_{n+1}$ 。叶子结点没有孩子，所以它们的 $p_i$ 属性没有定义。

3. 关键字 $x.key_i$ 对存储的各子树中的关键字范围加以分割：如果用 $k_i$ 来表示由 $x.p_i$ 所指向的一棵子树中的关键字，则有

$k_1\leq x.key_1\leq k_2\leq x.key_2\leq \cdots \leq x.key_n\leq k_{n+1}$

4. 所有叶子结点都出现在同一层，换言之，每个叶子结点具有相同的深度，即树高 $h$ 。

5. 每个结点所包含的关键字个数有上界和下界，这些界与一个固定的不小于2的整数t有关，t被称为B树的最小度数（minmum degree）。

a）除了根结点以外的每个结点必须至少有 $t-1$ 个关键字。因此，除了根结点以外的每个内部结点至少有t个孩子。如果树非空，则根节点至少有一个关键字。若根结点不是叶子结点，则至少有2个孩子（特殊情况：没有孩子的根结点，即根结点为叶子结点，整棵树只有一个根节点）；
b）每个结点最多可包含有 $2t-1$ 个关键字。因此，一个内部结点最多可以有 $2t$ 个孩子。当一个结点恰好有 $2t-1$ 个关键字时，该结点是满的（full）。

t=2时的B树是最简单的。每个内部结点有2、3或者4个孩子，此时我们称这种特殊的B树为2-3-4树。然而，在实际中t的值越大，B树的高度就越小。

上面这个定义来自《算法导论》，它是基于最小度数t来给出的。另外一种常见的定义是基于阶m给出的，如下（注意这两种定义是完全等价的）：

每个结点最多有 m 个孩子。

每个非叶子结点（除了根以外）至少有 $\left \lceil m/2 \right \rceil$ 个孩子。

若根结点不是叶子结点，则至少有2个孩子（特殊情况：没有孩子的根结点，即根结点为叶子结点，整棵树只有一个根节点）。

一个有n+1个孩子的非叶子结点包含有n个关键字。

所有叶子结点都出现在同一层，换言之，每个叶子结点具有相同的深度，即树高 $h$ 。

可见，在第一种基于度数t的定义中，除了根节点以外的每个内部结点所包含之孩子数量x为 $t\leq x\leq 2t$ ；而在第二种基于阶m的定义中， $\left \lceil m/2 \right \rceil\leq x\leq m$ 。

二、在B树中进行搜索

在一棵B树中进行搜索和在一棵二叉树中进行搜索差不多，只是在每个结点中所做的不是二叉分支，而是根据结点中孩子的数量进行多路分支选择。从根节点开始，从上到下递归的遍历树。在每一层上，搜索的范围被减小到包含了搜索值的子树中。子树值的范围被它的父节点的键确定。

B树中的搜索算法B-TREE-SEARCH(x, k)的输入是一个指向根节点x的指针，以及要在该子树中搜索的一个目标关键字k。因此，最开始的调用形式为B-TREE-SEARCH(T.root, k)。如果k在B树中，则返回由结点 $y$ 和使得 $y.key_i=k$ 的下标i所组成的有序对(y, i)；否则，如果找不到，则返回空。

B-TREE-SEARCH(x, k)

i = 1

while $i\leq x.n$ and $k > x.key_i$ //找出最小下标i，使得 $k > x.key_i$

i = i + 1 //如果找不到，则i被置为x.n+1

if $i\leq x.n$ and $x == x.key_i$ //检查是否在该结点x中已经找到关键字

return (x, i) //如果找到，则返回

elseif x is a leaf //如果找不到，并且x已经是叶子结点

return NIL //表明树中不存在该关键字，则返回空

else return B-TREE-SEARCH( $x.c_i, k$ ) //如果x不是叶子结点，则递归地在子树中进行搜索

本文最开始时给出的示例图片演示了这一搜索过程，此处不再详表。

三、在B树中插入关键字

为了构造一棵Ｂ树Ｔ，需要先使用B-TREE-CREATE来创建一个空的根结点，然后调用B-TREE-INSERT来添加新的关键字。来看下面的伪代码，它读入一个空结点x，并令其为新建之树Ｔ的根：

B-TREE-CREATE(T, x)

x.leaf = TRUE

x.n = 0

T.root = x

向Ｂ树中插入一个关键字要比向二叉树插入一个关键字复杂许多。在二叉树中，需要先找到可以插入新关键字的叶子结点的位置，再为新关键字创建一个新的（叶子）结点。但在Ｂ树中不能简单地创建一个新的叶子结点，然后就将新关键字插入，因为这样会破坏Ｂ树的合法性。我们需要将新的关键字插入到一个已经存在的叶子结点上。但是我们又不能将关键词插入到一个已经满了的叶子结点上，因此引入一个分裂操作，将满的结点（已有2t-1个关键字） $y$ 按其中位关键字（median key） $y.key_t$ 分成（split）两个各含 t-1个关键字的结点。中间关键字被提升到 $y$ 的父结点，以标识两棵新树的划分点。但是如果 $y$ 的父结点也是满的，就必须在插入新的关键字之前将其分裂，最终满结点的分裂会沿着树向上传播。

与一棵二叉树类似，可以在从树根到叶子这个单程向下的过程中将一个新的关键字插入B树中。为了做到这一点，我们并不是等到找出插入过程中实际要分裂的满结点时才做分裂。相反，当沿着树往下査找新的关键字所属位置时，就分裂沿途遇到的每个满结点（包括叶结点本身）。因此，每当要分裂一个满结点y时，就能确保它的父结点不是满的。

函数B-TREE-SPLIT-CHILD的输入是一个非满的内部结点 $x$ 和一个下标 $i$ ，由 $i$ 给出的 $x.c_i$ 为 $x$ 的一个满子结点（full child）。B-TREE-SPLIT-CHILD把这个子结点 $x.c_i$ 分裂成两个，并调整 $x$ ，使之包含多出来的孩子。要分裂一个满的根，首先要让根成为一个新的空根结点的孩子，这样才能使用B-TREE-SPLIT-CHILD。树的高度因此增加1，对根进行分裂是B树长高的唯一途径。

下图是分裂Ｂ树中结点的一个例子，在这个例子中t=4，也就是说在这棵Ｂ树里，每个结点最多可包含有７个关键字。满结点 $y=x.c_i$ 按照其中位关键字Ｓ进行分裂，Ｓ被提升到y的父结点 $x$ 。y中的那些大于中位关键字的关键字都被放在一个新的结点z中，它成为 $x$ 的一个新孩子。

下面给出B-TREE-SPLIT-CHILD的伪代码。

B-TREE-SPLIT-CHILD(x, i)

$y=x.c_i$

z.leaf = y.leaf    //如果y是一个叶子，那么新建的结点z也是一个叶子，反之亦然

z.n = t - 1　　　　　　　 //新建的结点z中应该包含的关键字数量为n-1

for j = 1 to t - 1　　　　    //为新建的结点z赋新的关键字，这些关键字是y中大于中位数的那些关键字

   $z.key_j = y.key_{j+t}$

if y is not a leaf　　　　　 //如果y不是叶子，那么新建的结点z也不是一个叶子

  for j = 1 to t　　　　　 //所以把y中的一部分孩子转移到z下面

   $z.c_j = y.c_{j+t}$

y.n = t - 1 //因为y中已经分离了一部分孩子和关键字给z，所以调整y.n的值

for j = x.n + 1 downto i + 1　//x中插入了一个新的关键字，所以i+1后的每个孩子都相应后移

   $x.c_{j+1} = x.c_j$

$x.c_{i+1} = z$

for j = x.n downto i　　　　//x中的关键字也相应后移

   $x.key_{j+1} = x.key_j$

x.key_i = y.key_t

x.n = x.n + 1　　　　　　　//因为x中多了一个关键字，调整x.n的值

这里x是被分裂的结点，y是x的第i个孩子。开始时，结点y有2t个孩子（2t-1个关键字），在分裂后减少至 $t$ 个孩子（ $t-1$ 个关键字）。结点z取走y的 $t$ 个最大的孩子（ $t-1$ 个关键字），并且z成为x的新孩子，它在x的孩子表中仅位于y之后。y的中间关键字上升到x中，成为分隔y和z的关键字。第1〜8行创建结点z，并将y的t-1个关键字以及相应的t个孩子转移它。第9行调整y的关键字个数。最后，第10〜16行将z插入为x的一个孩子，并提升y的中位关键字到x来分隔y和z，然后调整x的关键字个数。

在一棵B树T中，以沿树单程下行（也就是从根到叶子）的方式插入一个关键字k的操作B-TREE-INSERT利用B-TREE-SPLIT-CHILD 来保证递归始终不会降至一个满结点上。下面给出B-TREE-INSERT函数的伪代码：

B-TREE-INSERT(T, k)

r = T.root

if r.n == 2t - 1

   T.root = s

   s.leaf = FALSE

   s.n = 0

   $s.c_1 = r$

   B-TREE-SPLIT_CHILD(s, 1)

   B-TREE-INSERT-NONFULL(s,k)

else B-TREE-INSERT-NONFULL(r,k)

由于插入操作是沿树单程下行的，所以第一行，先考察根的情况。代码中的3～8行处理了结点r为满的情况。最开始，如果根是满的，那么按照前面讲的：需要对根进行分裂，而分裂一个满的根，首先要让根成为一个新的空根结点的孩子。所以我们引入了一个空节点s来作为新的根。前面已经讲过：函数B-TREE-SPLIT-CHILD的输入是一个非满的内部结点 $x$ 和一个下标 $i$ ，由 $i$ 给出的 $x.c_i$ 为 $x$ 的一个满子结点（full child）。B-TREE-SPLIT-CHILD把这个子结点 $x.c_i$ 分裂成两个，并调整 $x$ ，使之包含多出来的孩子。现在的情况就是原来的r节点是满的，所以建立一个空节点s来作为新的根（相当于 $x$ ），空节点s只有一个满的孩子r（ $x.c_i$ ），所以我们调用B-TREE-SPLIT-CHILD来对 $s.c_1$ （也就是r）进行分裂。分裂之后新的根s将不会是一个满的节点，所以这时便可以调用B-TREE-INSERT-NONFULL(s,k)来将关键字k插入了。但是，如果根节点r本来就不是满的，则直接调研INSERT-NONFULL(r,k)来将关键字k插入（第9行）。

例如，下图给出了一个t=4的根结点，它最多能容纳7个关键字，所图中的r最开始就是满的。对其进行分裂，即将r一分为二，并创建一个新的结点s。新的根包含了r的中位关键字，且以r的两半作为左右两个孩子。当根被分裂时，B树的高度加一。

上面的函数中，通过调用B-TREE-INSERT-NONFULL来完成将关键字k插入以非满的结点为根的树中。B-TREE-INSERT-NONFULL在需要时沿树向下递归，在必要时通过调用B-TREE-SPLIT-CHILD来保证任何时刻它所递归处理的结点都是非满的。B-TREE-INSERT-NONFULL是基于递归实现的，它将关键字k插入结点x，并假定在调用过程时x是非满的。操作B-TREE-INSERT和B-TREE-INSERT-NONFULL的递归执行保证了这个假设的成立。下面给出B-TREE-INSERT-NONFULL的伪代码：

B-TREE-INSERT-NONFULL(x, k)

i = x.n

if x is a leaf

   while $i\geq 1$ and $k < x.key_i$

       $x.key_{i+1} = x.key_i$

       i = i - 1

   $x.key_{i+1} = k$

   x.n = x.n + 1

else while $i\geq 1$ and $k < x.key_i$

       i = i - 1

   i = i + 1

   if $x.c_i.n == 2t - 1$

       B-TREE-SPLIT-CHILD(x, i)

       if $k > x.key_i$

           i = i + 1

   B-TREE-INSERT-NONFULL( $x.c_i, k$ )

现在来审视一下B-TREE-INSERT-NONFULL的实现细节。第３～７行处理x是叶子的情况，将关键字 $k$ 插入 $x$ 。如果 $x$ 不是叶子，则必须将 $k$ 插入以内部结点 $x$ 为根的子树中适当的叶结点中去。从第8～10行的处理中可以看到，如果 $x.key_{i-1}<k<x.key_i$ ，其中 $i\geq 2$ ，那么 $k$ 将被插入子树 $x.c_i$ 中；或者 $k<x.key_1$ ，那么 $k$ 将被插入子树 $x.c_1$ 。但必须确保 $x.c_i$ 不是满的，其中 $i\geq 1$ ，为此第11～12行表示如果 $x.c_i$ 是满的，则将该子结点分裂成两个非满的孩子。第13～14行确定向刚刚分裂出来的两个孩子中的哪一个进行下降。最后，第15行递归第将 $k$ 插入到合适的子树中。

最后给出一个具体的例子，如下图所示，依次向B树中插入关键字B、Q、L、F。这棵B树的初始状态如图（a）所示，它的最小度数t为3，所以一个结点至多可包含5个关键字。在插入过程中被修改的结点由浅色阴影标记。首先，试着向图（a）所示的树中插入关键字B。此时根节点不是满的，无需对根节点做分裂，直接走B-TREE-INSERT中的第9行，调用B-TREE-INSERT-NONFULL，结果如图（b）所示。

接下来，在图（b）的基础上插入关键字Q。同样，开始时根节点不是满的，无需对根节点做分裂，直接走B-TREE-INSERT中的第9行，调用B-TREE-INSERT-NONFULL，但是包含RSTUV的结点是满的。因此，结点RSTUV被分裂为两个分别包含RS和UV的结点。关键字T被提升到父结点（本例中也就是根）中。Q被插入到两棵新子树中左边的一棵的最左边（RS结点中的左边），结果如图（c）所示。

再然后，继续试着将L插入前一棵树中。由于此时图（c）中的根结点是满的，所以要执行B-TREE-INSERT中的3～8行，也就是对根进行分裂，同时B树的高度增加1。然后，根结点不再是满的，则调用B-TREE-INSERT-NONFULL，于是L被插入包含KJ的叶结点中。结果如图（d）所示。

最后，试着将F插人前一棵树中。此时，根节点不是满的，无需对根节点做分裂，直接走B-TREE-INSERT中的第9行，调用B-TREE-INSERT-NONFULL，但是包含ABCDE的结点是满的。结点 ABCDE会进行分裂，中位关键字C会被提升到父结点中。然后，F就可以被插入到新得到的两棵子树中的右边一棵的最右边（DE结点的右边），最终结果如图（e）所示。

四、从B树中删除关键字

通过前面的介绍，读者已经知道，B树上插入操作只能够在叶结点上操作。B树上的删除操作总体上与插入操作类似，但要略微复杂一点，因为我们允许从任意一个结点（不一定是叶结点）中删除一个关键字，而且当从一个内部结点删除一个关键字时，还要重新安排这个结点的核子。与插入操作一样，必须防止因删除操作而导致树的结构违反B树性质。就像必须保证一个结点不会因为插入而变得太大一样，必须保证一个结点不会在删除期间变得太小（根结点除外，因为它允许有比最少关键字数t-1还少的关键字个数）。一个简单插入算法，如果插入关键字的路径上结点满，可能需要向上回溯；与此类似，一个简单删除算法，当要删除关键字的路径上之结点（非根）有最少的关键字个数时，也可能需要向上冋溯。

函数B-TREE-DELETE从以x为根的子树中删除关键字k。我们设计的这个过程必须保证无论怎样，结点x递归调用自身时，x中关键字个数至少为最小度数 $t$ ，注意Ｂ的性质要求：除了根节点以外的每个内部结点必须至少有 $t-1$ 个关键字（所包含之孩子数量x为 $t\leq x\leq 2t$ ）。所以，值得注意的是，现在的这个条件要求比通常B树中的最少关键字个数多一个以上。这将导致有时在递归下降至子结点之前，需要把一个关键字移到子结点中。这个加强的条件允许在一趟下降过程中，就可以将一个关键字从树中删除，（如无特殊情况就）无需任何“向上回溯”。

现在简要地介绍删除操作是如何工作的：
1. 如果关键字k在结点x中，并且x是叶结点，则从x中删除k。
2. 如果关键字k在结点x中，并且x是内部结点，则做以下操作：

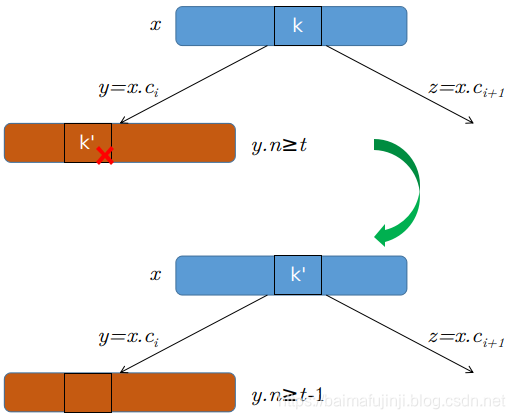
a）如果结点x中前于k的子结点y，至少包含 $t$ 个关键字，则找出k在以y为根的子树中的前驱k'。递归地删除k'，并在x中用k'代替k。（找到k'并删除它可在沿树下降的单向过程中完成。）如图４－(a) 所示。
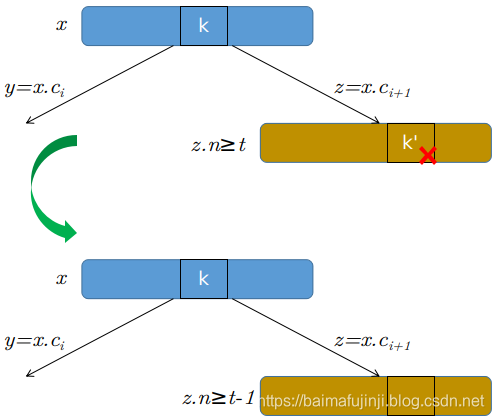
b）对称地，如果y有少于 $t$ 个关键字，则检査结点x中后于k的子结点z。如果z至少有 $t$ 个关键字，则找出k在以z为根的子树中的后继k'。递归地删除k'，并在x中用k'代替k。（找到并删除它可在沿树下降的单向过程中完成。）如图４－(b) 所示。
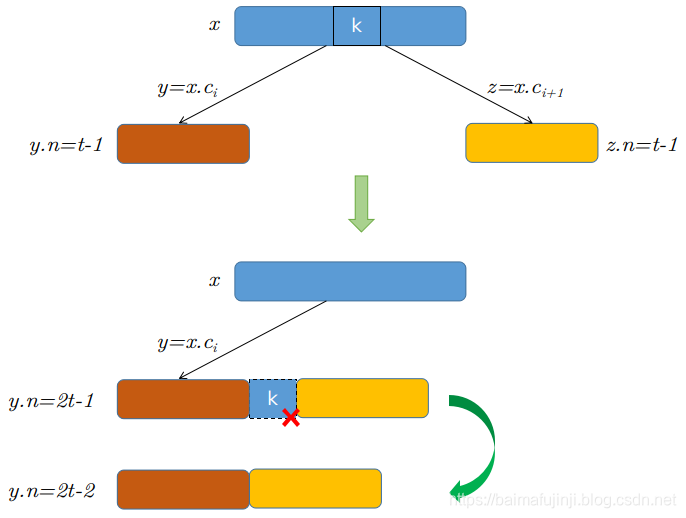
c）否则，如果y和z都只含有 $t-1$ 个关键字，则将k和z的全部合并进y，这样x就失去了k和指向z的指针，并且，现在y包含 $2t-1$ 个关键字。然后释放z并递归地从y中删除k。如图４－(c) 所示。

3. 如果关键字k当前不在内部结点x中，则确定必包含k的子树的根 $x.c_i$ （如果k确实在树中）。如果 $x.c_i$ 只有 $t-1$ 个关键字，必须执行步骤3a或3b来保证降至一个至少包含t个关键字的结点。然后，通过对x的某个合适的子结点进行递归而结束。

a）如果 $x.c_i$ 只含有 $t-1$ 个关键字，但是它的一个相邻的兄弟至少包含 $t$ 个关键字，则将x中的某一个关键字降至 $x.c_i$ 中，将 $x.c_i$ 的相邻左兄弟或右兄弟的一个关键字升至 $x$ ，将该兄弟中相应的孩子指针移到 $x.c_i$ 中，这样就使得 $x.c_i$ 增加了一个额外的关键字。
b）如果 $x.c_i$ 以及 $x.c_i$ 的所有相邻兄弟都只包含 $t-1$ 个关键字，则将 $x.c_i$ 与一个兄弟合并，即将 $x$ 的一个关键字移至新合并的结点，使之成为该结点的中位关键字。

最后给出一个具体的例子，如下图所示，从一棵B树中依次删除关键字Ｆ、Ｍ、Ｇ、Ｄ、Ｂ。这棵B树的最小度数 $t=3$ ，因此一个结点（非根）包含的关键字个数不能少于两个。被修改了的结点都以浅色阴影标记。最初的Ｂ树如图（a）所示。首先，如图（b）所示，要删除的关键字Ｆ位于叶子结点中，所以直接将其删除。接下来，要删除关键字Ｍ，但是它位于一个内部结点中，而且它的前驱孩子ＪＫＬ中的关键字数量为３。因此删除Ｍ，并将它在左孩子中的前驱Ｌ提升并占据M的位置，结果如图（c）所示。再然后，试着删除关键字Ｇ，它位于一个内部结点中，而且它左右两侧的孩子都有２个关键字。显然这属于是２c所描述的情况。于是将G下降，并连同右孩子ＪＫ一起并入左孩子ＤＥ中，构成结点DEGJK，然后从这个叶结点中删除G（也就是１所示描述的叶子结点的情况）。

现在来尝试删除关键字D。从根结点r开始，Ｄ不在结点r中，包含D的子树的根是CL结点，该结点中只有２个关键字，而且它的相邻的兄弟结点TX也只包含２个关键字，因此属于3b的情况。递归不能降至结点CL，因为它仅有两个关键字，所以将r中的一个关键字Ｐ下降并与CL和TX合并以构成CLPTX；然后就又变成了情况1，随即将D从这个叶结点中删除。得到如图（e）所示的结果。更进一步，如图（e'）所示，因为新得到的根节点为空，所以将其删除，树的高度减小1。最后，尝试删除关键字Ｂ。这属于3a所描述的情况：移动C以填补B的位置，移动E以填补C的位置。所得之结果如图（f）所示。

由于一棵B树中的大部分关键字都在叶结点中，可以预期在实际中，删除操作最经常用于从叶结点中删除关键字。这样B-TREE-DELETE过程只要沿树下降一趟即可，不需要向上回溯。然而，当要删除某个内部结点的关键字时，该过程也要沿树下降一趟，但可能还要返回删除了关键字的那个结点，以用其前驱或后继来取代被删除的关键字（情况2a和情况2b）。此外，在B树上进行删除操作的设计也是从下面这个大原则上考虑的：如果根结点x成为一个不含任何关键字的内部结点，那么x就要被删除，x的唯一孩子 $x.c_1$ 成为树的新根，从而树的高度降低1，同时也维持树根必须包含至少一个关键字的性质（除非树是空的）。

*本文主要参考《算法导论（第三版）》第18章，其中忽略了关于存储器读写部分的细节。

白马负金羁博客专家

发布了358 篇原创文章 · 获赞 4280 · 访问量 417万+

他的留言板关注