十、【数据结构】B-树(B-tree)的解析与实现

版权声明：本文为博主原创文章，未经博主允许不得转载。 https://blog.csdn.net/qq_18108083/article/details/84982186

一、B-树的出发点

任何一种数据结构的产生都不是毫无根据凭空想象出来的，一般而言它们都是为了解决某种问题才被设计。B-树的产生主要是解决数据库查找时候对外存的访问次数的。我们知道，第一台电脑只有一万多个电子管，而现在一个硬盘都能TB的存储量级，可以说到目前为止计算机的存储能力已经有了巨大的提升。但是实际上人们对存储空间需求的增长更加迅速，现在的大型数据库都需要以TB为单位来计量，而我们知道，在相同成本下，存储器的容量越大则访问速度越慢，因此一味地提高存储能力并不能解决访问速度的问题。

分级存储的策略是很有效的，在由内存和外存（硬盘）组成的耳机存储系统中，数据全集往往放在外存中，计算过程中将内存作为外存的高速缓存，存放最常用数据项的副本，这样就能将“高速度”和“大容量”结合起来。

两个向量级别之间的数据传输称为I/O操作。由于内存的访问速度和硬盘的访问速度存在ns到ms的巨大差距（硬盘访问一次的时间内内存可以访问10^6次）。所以在程序运行的过程中我们不希望有过多的I/O操作（如北京的学校里面粉笔没用完，则不会经常去广东买新的），事实上在这种巨大差异的背景下，我们衡量算法的性能时，基本可以忽略对内存的访问，更多地关注多外存的访问次数。

当数据规模大到基本上都存储在外存中时，常规平衡二叉树的效率往往大打则扣，原因是访问次数依然过多，例如对10亿条记录，若采用普通的AVL树，依靠二分查找策略，也需要大概30次（2^30≈10^9）。

多路搜索树：

事实上，我们可以利用硬盘的一个特性：就时间成本而言，读取物理地址连续的一千个字节，与读取单个字节几乎没有区别，即硬盘更适宜于批量访问。故我们可以把普通的二叉搜索树进行改造，将局部的多层节点安装中序遍历次序重新组成一个大节点，这样就很明显地把树的层数降低了，这时候算法在查找时，每次可从硬盘中取一个大节点到内存中，然后在内存中再对这个大节点的内部进行细致地查找，这样就很明显地降低了对外存的访问次数。

一般地，以k层为间隔进行重组，可将二叉搜索树转化为等价的2^k路搜索树。k数量的确定和不同外存的特性有关，若取k=8，则每个大节点拥有255个关键码和256个分支，同样对于1g个记录，每次查找将由30次缩减到4~5次（具体是缩减到原来的log2m分之一，m的取值经常在256~1024）！

可见，多路搜索策略能极大地降低对外存的访问次数，因此能极大地提升程序的效率。

二、B-树的定义

1970年， R.Bayer和E.mccreight提出了B树，所谓m阶B树，即m路平衡搜索树。（ 有些地方写的是B-树，注意不要误读成”B减树”）一棵M阶(M>=2)的B树， 是一棵平衡的M路平衡搜索树， 可以是空树或者满足一下性质：

1. 根节点至少有两个分支（根节点不受2的严格限制，因为当根节点上溢的时候，需要新建一个父节点作为新根，这时候根节点只有2个分支，无论B-树为多少阶都这样）。  

2. 每个非根节点的分支数范围为 [|M/2|(上取整)，M] ——假设M为3，则该节点至少有（(3+1)/2）个分支，至多有3个分支，故m阶B-树也被称作是（|m/2|(上取整),m）树。  

3. 每个非根节点内部的关键码数都是分支总数减一， 并且以升序排列  

4. key[i]和key[i+1]之间的孩子节点的值介于key[i]、 key[i+1]之间——B树为有序树，每两个键值之间的所有孩子节点的键值大小必然介于两双亲节点之间。

5. 所有的叶子节点都在同一层——B树不同于其他树从上向下生长，而是自下而上，层层分裂。

如图所示

三、B-树操作细节

1.search操作

鉴于B-树适合解决I/O访问问题，一般在实际中将大数据集以B树的形式存放于外存，对于活跃的B-树，其根节点往往放置于内存，此外，每次只有一个节点被拉入内存做细致查找。

性能分析：与二叉搜索树类似，B-树的每一查找过程，在每一高度上都至多访问一个节点，所以对于高度为h的B-树，外存访问不超过O(h-1)次。

而对于有N个关键码的m阶B-树而言，树的高度h=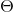(logm(N))(这里是确界，所以说B-树的高度变化不大)，故总耗时为O(logmN)。

2.insert操作(注意插入的是关键码而不是大节点)

基本操作：和二叉搜索树的插入一样，首先search找到要插入的位置（先search到目标节点，再search到在节点key向量中的的目标秩），然后直接插入到key中并添加一个空孩子到child向量中即可。

目标节点上溢：（分裂处理）

关键码的插入操作可能导致被插入节点的上溢，这时节点关键码的数量刚好为阶数m。B-树中对节点的上溢通过分裂进行处理：取该节点的中轴关键码（秩为m/2），以该中轴关键码为中心将节点分裂成左右两个节点，然后将中轴关键码插入到父节点对应的位置上，然后维护好节点之间的父子关系即可。

此后逐层对父节点进行上溢检查处理操作，直至未父节点未发生上溢或者到达根节点。若根节点上溢，则新建个节点作为父节点，树的高度加1（B-树增高的唯一途径）。

 

3.remove操作(注意删除的是关键码而不是大节点)

基本操作：和二叉搜索树的删除一样，关键码的删除分为两个情况：

(a) 关键码所在节点为叶节点，则直接删除即可。

(b) 关键码所在节点为为非根节点，则找到直接后继（必然在叶节点的最左侧），然后交换此关键码和直接后继关键码的数据，则并不破坏树的原来结构，只需要删除原直接后继关键码所在的位置即可。

目标节点下溢：（合并处理）

关键码的删除可能导致被删除节点的下溢，这时节点关键码的数量刚好是（|m/2|(上取整)-2）。B-树中对节点的下溢通过合并节点进行处理，分为3种情况:

(a) 下溢节点的左兄弟存在，且至少包含|m/2|(上取整)个关键码

这时下溢节点向父亲借一个关键码，父节点再向左兄弟借一个关键码，将左节点的最右孩子放到下溢节点的最左边。

(b) 下溢节点的右兄弟存在，且至少包含|m/2|(上取整)个关键码

这时下溢节点向父亲借一个关键码，父节点再向右节点借一个关键码，将右节点的最左孩子放到下溢节点的最右边，这个过程是上图所示过程的相反方向。

(c) 若左右兄弟节点都没有足够多的关键码借给下溢节点

这时下溢节点与左兄弟（若存在）或者右兄弟（若存在）合并，具体是从父节点中找到父关键码，下移，以其为根关键码拼接两个节点。

此后逐层对父节点进行下溢检查处理操作，直至未父节点未发生下溢或者到达根节点。若根节点下溢为空，则删掉这个根节点即可，其子孩子为新根，树的高度减1（这也是B-树高度减小的唯一途径）。

四、B-树的性能

B-树查找、插入、删除的时间复杂度都和深度成线性关系，而对于有N个关键码的m阶B-树而言，树的高度h=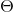(logm(N))(这里是确界，所以说B-树的高度变化不大)，故这些操作的耗时均为O(logmN)。

五、B-树的实现

B-树的实现包含bTNode类的实现和bTree类的实现，其中bTNode类主要是描述B-树中的大节点的颞部结构，包括其父类，包含的关键码向量和孩子节点向量。而bTree类主要是B-树的描述，包括树中关键码的总数，B-树的阶数，以及一些B-树的查找、插入、删除操作及上溢下溢处理操作。

bTNode接口列表

操作	功能	对象
bTNode()	默认构造函数（只在创建根节点时使用）
bTNode(T e, bTNode<T> *lc = nullptr, bTNode<T> *rc = nullptr)	构造函数（只在创建根节点时使用）

bTree接口列表

操作	功能	对象
bTree(int order=3)	构造函数，默认阶数为3
~bTree()	析构函数
order()	返回阶次	B-树
size()	返回存放的关键码的总数	B-树
root()	返回根节点的引用	B-树
empty(	判断是否为空	B-树
search(const T& e)	查找关键码	B-树
insert(const T& e)	插入关键码	B-树
remove(const T& e)	删除关键码	B-树
solveOverflow(bTNode<T>* v)	上溢分裂处理	B-树
solveUnderflow(bTNode<T>* v)	下溢合并处理	B-树

(1) bTNode.h

#pragma once
#include"vector.h"

template<typename T> struct bTNode
{
	bTNode<T>* parent;   //父类
	vector<T> key;   //关键码向量 (数量总比孩子向量少1)
	vector<bTNode<T>*> child;   //孩子向量  数量范围为[m/2,m)

	//构造函数
	bTNode();   //节点只作为根节点构造，且构造时首先在child向量中插入一个空孩子分支
	bTNode(T e, bTNode<T> *lc = nullptr, bTNode<T> *rc = nullptr);
};

template<typename T> bTNode<T>::bTNode()
{
	parent = nullptr;
	child.insert(0, NULL);
}

template<typename T> bTNode<T>::bTNode(T e, bTNode<T> *lc = nullptr, bTNode<T> *rc = nullptr)
{
	parent = nullptr;
	key.insert(0,e);
	child.insert(0, lc);
	child.insert(1, rc);
	if (lc) lc->parent = this;
	if (rc) rc->parent = this;
}

(2) bTree.h

#pragma once
#include"bTNode.h"

template<typename T> class bTree
{
protected:
	int _size;   //关键码的总数
	int _order;  //b-树的阶次，一般在设定后不在修改
	bTNode<T>* _root;  //根节点
	bTNode<T>* _hot;   //查找时指向最终命中节点的父亲
	void solveOverflow(bTNode<T>* v);   //上溢分裂处理
	void solveUnderflow(bTNode<T>* v);    //下溢合并处理

public:
	bTree(int order=3);
	~bTree();
	int const order();  //返回阶次
	int const size();   //返回存放的关键码的总数
	bTNode<T>* & root();  //返回根节点的引用
	bool empty() const;   //判断是否为空
	bTNode<T>* search(const T& e); //查找关键码
	bool insert(const T& e);   //插入关键码
	bool remove(const T& e);  //删除关键码
};

template<typename T> bTree<T>::bTree(int order = 3)
{
	_order = order;
	_size = 0;
	_root = new bTNode<T>();
}

template<typename T> bTree<T>::~bTree()
{
	if (_root)
		delete _root;
}

template<typename T> int const bTree<T>::order()
{
	return _order;
}

template<typename T> int const bTree<T>::size()
{
	return _size;
}

template<typename T> bTNode<T>* & bTree<T>::root()
{
	return _root;
}

template<typename T> bool bTree<T>::empty() const
{
	return !_root;
}

template<typename T> bTNode<T>* bTree<T>::search(const T& e)
{
	Rank r;
	bTNode<T>* v = _root; _hot = nullptr;
	while (v) //逐层查找
	{
		r = v->key.search(e);
		if ((r >= 0) && (v->key[r] == e)) return v;   //查找成功
		 _hot = v;  v = v->child[r + 1];   //本层没查到，转到合适的孩子节点继续查找                          
	}
	return nullptr;
}

template<typename T> bool bTree<T>::insert(const T& e)
{
	bTNode<T>* v = search(e);
	if (v) return false;  //已存在则返回,否则_hot为最终查找失败的节点的父节点
	Rank r = _hot->key.search(e);  //返回直接前续关键码的索引,就插在它后面
	_hot->key.insert(r + 1, e);
	_hot->child.insert(r + 2, nullptr);
	_size++;
	solveOverflow(_hot); //从本节点开始向上检查上溢现象并修复
	return true;
}

template<typename T> void bTree<T>::solveOverflow(bTNode<T>* v)
{
	if (v->child.size() <= _order) return;  //未发生上溢，则返回  (除根节点外每个节点的孩子引用数:[m/2,m))
	//处理方法，从中轴处分裂节点v成两个节点，中轴关键码插入到父节点中
	Rank s = _order/2;					//r为中轴关键码的秩(此时child.size()为b-树阶数)
	bTNode<T>* u = new bTNode<T>();		 //新建一个节点，用来作为右半边
	//转移数据
	for (int i = 0; i < _order  - s - 1; i++)
	{
		u->key.insert(i, v->key.remove(s + 1));  //转移右半边的关键码
		u->child.insert(i, v->child.remove(s + 1));
	}
	u->child[_order-s-1] = v->child.remove(s + 1);     //v节点最靠右的孩子
	if (u->child[0])  //若u的孩子非空,更新孩子指向
		for (int i = 0; i < (u->child.size()); i++)
			(u->child[i])->parent = u;
	//插入父节点
	bTNode<T>* p = v->parent;
	if (!p)  //若父节点不存在，则新建
	{
		_root = p = new bTNode<T>(); p->child[0] = v; v->parent = p;
	}
	Rank r = p->key.search(v->key[s]);  //寻找插入点
	p->key.insert(r + 1, v->key.remove(s));  //将中轴点插入父节点
	p->child.insert(r + 2, u); u->parent = p;
	solveOverflow(p);
}

template<typename T> bool bTree<T>::remove(const T& e)
{
	
	bTNode<T>* v = search(e);
	if (!v) return false;   //若e不存在则直接返回
	Rank r = v->key.search(e);   //r为关键码对应的秩
	if (v->child[0])     //类似普通二叉搜索树，若待删除的关键码所在节点非叶节点，则找到关键码的直接后继进行数据交换，删除这个直接后继即可，若v非叶节点，则e的后续必属于叶节点(且为最左端)
	{
		bTNode<T>* u = v->child[r + 1];
		while (u->child[0])
			u = u->child[0];     //一直找到其直接后继(最左端)
		v->key[r] = u->key[0];   //替换值
		v = u;  r = 0;  //v为仍为实际要删除的关键码，方便统一处理
	}
	//统一删除
	v->key.remove(r);
	v->child.remove(r + 1);
	_size--;
	solveUnderflow(v);
	return true;
}


template<typename T> void bTree<T>::solveUnderflow(bTNode<T>* v)
{
	if (v->child.size() >= (_order + 1) / 2) return;  //未发生下溢，返回
	//分3种情况处理
	bTNode<T>* p = v->parent;
	if (!p)  //v为根节点
	{
		if ((!v->key.size()) && (v->child[0])) //若该根节点并无有效关键码，只是有孩子节点，则删除，整树上移
		{
			_root = v->child[0];
			_root->parent = nullptr;
			v->child[0] = nullptr;   delete v; v = nullptr;
		}
		return;
	}
	Rank r = 0;
	while (p->child[r] != v)    //找到v在父节点中child中向量中的秩，方便寻找其左右兄弟
	{
		r++;
	}

	//case 1: 下溢节点的左兄弟有足够多的关键码，通过父关键码右移补充
	if (0 < r)  //有左兄弟
	{
		bTNode<T>* ls = p->child[r - 1];  //左兄弟
		if (ls->child.size() >= ((_order + 1) / 2) + 1)   //此左兄弟有足够多的关键码
		{
			v->key.insert(0, p->key[r - 1]);  //先从v的父节点中借用关键码
			v->child.insert(0, ls->child.remove(ls->child.size() - 1));  //挂载子树节点到最左端
			p->key[r - 1] = ls->key.remove(ls->key.size() - 1);  //左兄弟牺牲的关键码移动到父节点
			if (v->child[0]) v->child[0]->parent = v;
			return;
		}
	}//就算有左兄弟但是无多余的关键码也不发生动作

	//case 2: 下溢节点的右兄弟有足够多的关键码，通过父关键码左移补充
	if (r < (p->child.size() - 1))  //有右兄弟
	{
		bTNode<T>* rs = p->child[r + 1];  //右兄弟
		if (rs->child.size() >= ((_order + 1) / 2) + 1)  //此右兄弟有足够多的关键码
		{
			v->key.insert(v->key.size(), p->key[r]);
			v->child.insert(v->child.size(), rs->child.remove(0));
			p->key[r] = rs->key.remove(0);
			if (v->child[v->child.size() - 1])
				v->child[v->child.size() - 1]->parent = v;
			return;
		}
	}
	//case 3: 下溢节点的左右兄弟都没有足够多的关键码，这时父关键码下来，下溢节点与做或右节点组合形成新节点
	//左右两兄弟的关键码数量都不够，或者只存在一个兄弟且其数量不够,合并后可能会发生下溢传递
	if (r > 0)  //存在左兄弟，就和它合并
	{
		bTNode<T>* ls = p->child[r - 1];  //左兄弟
		ls->key.insert(ls->key.size(), p->key.remove(r - 1));   //父节点中的关键码下移
		p->child.remove(r); 
		//开始转移，把v中的关键码和孩子都转移到左兄弟中
		ls->child.insert(ls->child.size(), v->child.remove(0));
		if (ls->child[ls->child.size() - 1]) 
			ls->child[ls->child.size() - 1]->parent = ls;
		while (v->key.size())
		{
			ls->key.insert(ls->key.size(), v->key.remove(0));
			ls->child.insert(ls->child.size(), v->child.remove(0));
			if (ls->child[ls->child.size() - 1]) 
				ls->child[ls->child.size() - 1]->parent = ls;
		}
		delete v; v = nullptr;
	}
	else  //肯定存在右兄弟，就和它合并
	{
		bTNode<T>* rs = p->child[r + 1];  //右兄弟
		rs->key.insert(0, p->key.remove(r));   //父节点中的关键码下移
		p->child.remove(r);
		//开始转移，把v中的关键码和孩子都转移到右兄弟中
		rs->child.insert(0, v->child.remove(v->child.size() - 1));
		if (rs->child[0])
			rs->child[0]->parent = rs;
		while (v->key.size())
		{
			rs->key.insert(0, v->key.remove(v->key.size() - 1));
			rs->child.insert(0, v->child.remove(v->child.size() - 1));
			if (rs->child[0])
				rs->child[0]->parent = rs;
		}
		delete v; v = nullptr;
	}
	solveUnderflow(p);
	return;
}