\(0.\) RMQ问题
人话翻译
给定一个长度为\(n\)的数列\(a\),然后有\(m\)组询问,每次询问一个区间\([l,r]\)的最小值。
其中\(m,n\leq10^5\)
\(1.\) 暴力做法
很显然,暴力做法就是便历 \(\max\limits_{l\leq i\leq r}a_i\) 。这个做法最坏时间复杂度将会高达\(O(n^2)\)。很显然,这对于\(1e5\)的数据范围要炸
\(2.\) 正解
线段树
如果不知道什么是线段树,请点击这里 线段树
对于这种区间信息,线段树显然是能够维护的。但鉴于本题没有区间修改,线段树显然有点大材小用,并且数组模拟的线段树空间将会达到\(O(4n)\)
线段树还有一些缺点,就是它的查询时间复杂度最坏是\(O(logn)\)的,因为没有区间修改,这个时间开销也略微有点大。
\(ST\)表(倍增)
倍增算法的含义就是成倍增长。我们考虑一个这样的数据结构:
一个二维数组\(st\),其中
\[st_{i,j}=\min\limits_{i\leq k\leq i+2^j}a_k\]
我们假设一个数据:\(9\ 3\ 1\ 7\ 5\ 6\ 0\ 8\)
可以建立如下所示的\(ST\)表:
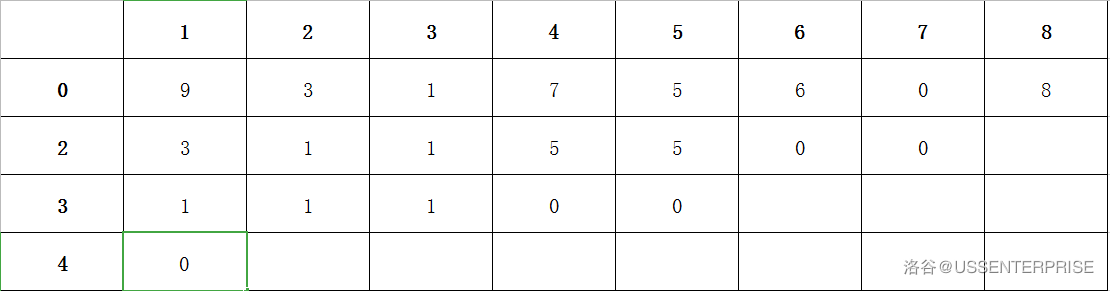
建表
我们发现,我们可以一层层地建表。这样,我们就可以通过递推,利用上层的信息,建表。
我们先将读入数据存在\(0\)这一行。
我们发现,要想实现建立这个表,我们需要每次倍增长度。而最简单的倍增长度方法就是将两段不相交的区间合并起来。
所以我们可以得到如下公式:
\[st_{i,j}=min(st_{i,j-1},st_{i+2^{j-1},j-1}\]
这样,我们就能完成建表
for(rg int i=1;i<=16;i++){ // 由计算器可得 log1e5 约为 17,但是这里循环16次已经够了。
for(rg int j=1;j+(1<<i)-1<=n;j++){
st[i][j]=min(st[i-1][j],st[i-1][j+(1<<(i-1))]);
}
}- 注:为了方便,我们常常把这个表“竖”过来。本篇中的代码一律如此
我们可以发现,建表的时间复杂度是\(O(nlogn)\)的
查询
我们由上表知道,想要查询\([l,r]\)的最值,只需求出
\[ min(st_{l,log(len)},st_{r-2^{log(len)+1},log(len)})\]
其中
\[ len=r-l+1 \]
比如上方的数据,我们想要查询\([3,8]\)
我们只需要从\(3\)往后\(4\)个,\(8\) 往前\(4\)个,肯定能够完全覆盖这个区间
所以我们的查询开销是\(O(1)\)的
ans=min(st[(int)log2(len)][l],st[(int)log2(len)][r-(1<<((int)log2(len)))+1]);至此,我们已经完成了全部内容