Preface

Jensen’s Inequality（Jensen不等式）
Expectation-Maximization Algorithm（EM算法）

Jensen’s Inequality

对于凸函数

令 $f(x)$ 为一个凸函数，且如果它有二阶导数，其二阶导数恒大于等于0（ $f(x)^{''} \geq 0$ ）。令 $x$ 为一个随机变量，那么：

\begin{aligned} E [f (x)] \geq f (E X) \end{aligned}

$\begin{aligned} E[f(x)]\ge f(EX) \end{aligned}$
这个不等式的含义如下图所示：
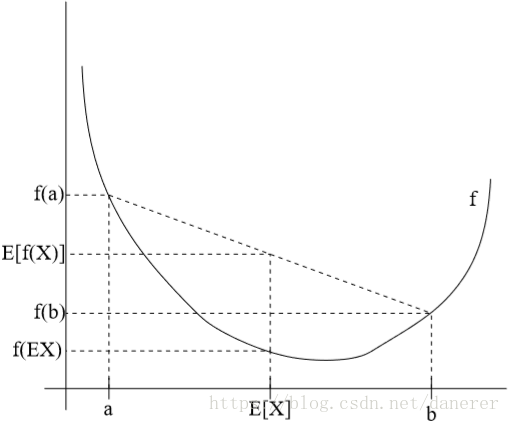
这里写图片描述

我们可以进一步推导出，如果

f (x)^{^{″}} > 0

$f(x)^{''}> 0$ ，即

f (x)

$f(x)$ 为一个严格的凸函数。那么：

\begin{aligned} E [f (x)] = f (E X) & ⟺ x 为常量的概率为1 \\ ⟺ X = E X 的概率为1 \end{aligned}

$\begin{aligned} E[f(x)]= f(EX) \;&\iff\;x \;\text{为常量的概率为1}\\ &\iff \;X=EX\;\text{的概率为1} \end{aligned}$

对于凹函数

如果 $f(x)^{''}\leq0$ ，即 $f(x)$ 为一个凸函数。那么：

\begin{aligned} f (E X) \geq E [f (x)] \end{aligned}

$\begin{aligned} f(EX)\ge E[f(x)] \end{aligned}$

Expectation-Maximization Algorithm

问题定义

假设训练集 $\{x^{(1)},x^{(2)},...,x^{(m)}\}$ 是由m个独立的无标记样本构成。我们有这个训练集的概率分布模型 $p(x,z;\theta)$ ，但是我们只能观察到 $x$ 。我们需要使参数 $\theta$ 的对数似然性最大化，即：

\begin{aligned} arg max_{θ} l (θ) & = arg max_{θ} \underset{i = 1}{\sum^{m}} l o g p (x^{(i)}; θ) \\ = arg max_{θ} \underset{i = 1}{\sum^{m}} l o g \sum_{z} p (x^{(i)}, z^{(i)}; θ) \end{aligned}

$\begin{aligned} \text{arg}\;\;\underset{\theta}{\text{max}}\;\;l(\theta)&=\text{arg}\;\;\underset{\theta}{\text{max}}\;\;\underset{i=1}{\overset{m}{\sum}}log\;p(x^{(i)};\theta)\\ &=\text{arg}\;\;\underset{\theta}{\text{max}}\;\;\underset{i=1}{\overset{m}{\sum}}log\underset{z}{\sum}p(x^{(i)},z^{(i)};\theta) \end{aligned}$

形式化过程

EM算法的过程大致如下：

首先，初始化 $\theta^{(0)}$ ，调整 $Q(z)$ 使得 $J(Q,\theta^{(0)})$ 与 $\theta^{(0)}$ 相等，然后求出 $J(Q,\theta^{(0)})$ 使得到最大值的 $\theta^{(1)}$ ；固定 $\theta^{(1)}$ ，调整 $J(Q,\theta^{(1)})$ ，使得 $J(Q,\theta^{(1)})$ 与 $\theta^{(1)}$ 相等，然后求出 $J(Q,\theta^{(1)})$ 使得到最大值的 $\theta^{(2)}$ ；……；如此循环，使得 $l(\theta)$ 的值不断上升，直到k次循环后，求出了 $l(\theta)$ 的最大值 $l(\theta^{(k)})$ 。

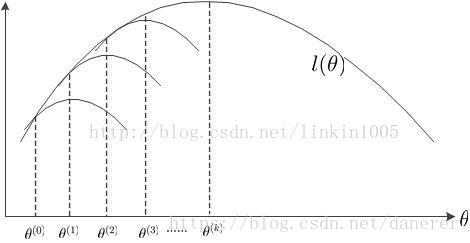
这里写图片描述

推导过程

在问题定义中我们知道：

\begin{aligned} arg max_{θ} l (θ) & = arg max_{θ} \underset{i = 1}{\sum^{m}} l o g p (x^{(i)}; θ) \\ = arg max_{θ} \underset{i = 1}{\sum^{m}} l o g \sum_{z} p (x^{(i)}, z^{(i)}; θ) \end{aligned}

假设每一个 $z^{(i)}$ 的分布函数为 $Q_i$ 。故有 $\sum_{Z}Q_{i}(z)=1,Q_{i}(z)\ge0$ 。所以：

\begin{aligned} l (θ) & = \sum_{i} l o g \sum_{z^{(i)}} p (x^{(i)}, z^{(i)}; θ) & (1) \\ = \sum_{i} l o g \sum_{z^{(i)}} Q_{i} (z^{(i)}) \frac{p (x^{(i)}, z^{(i)}; θ)}{Q_{i} (z^{(i)})} & (2) \\ \geq \sum_{i} \sum_{z^{(i)}} Q_{i} (z^{(i)}) l o g \frac{p (x^{(i)}, z^{(i)}; θ)}{Q_{i} (z^{(i)})} & (3) \end{aligned}

$\begin{aligned}l(\theta)&=\underset{i}{\sum}log\underset{z^{(i)}}{\sum}p(x^{(i)},z^{(i)};\theta)\quad\quad\quad\quad &(1)\\&=\underset{i}{\sum}log\underset{z^{(i)}}{\sum}Q_{i}(z^{(i)})\frac{p(x^{(i)},z^{(i)};\theta)}{Q_{i}(z^{(i)})}&(2)\\ &\ge \underset{i}{\sum}\underset{z^{(i)}}{\sum}Q_{i}(z^{(i)})log\frac{p(x^{(i)},z^{(i)};\theta)}{Q_{i}(z^{(i)})}&(3) \end{aligned}$
对于上述公式中的第（2）步到第（3）步的理解：

首先由于数学期望公式 $Y=g(X),g(X)为连续函数;E(Y)=E(g(x))=\prod_{k=1}^{\infty} g(x_{k})p_{k}$ ，
$\underset{z^{(i)}}{\sum}Q_{i}(z^{(i)})\frac{p(x^{(i)},z^{(i)};\theta)}{Q_{i}(z^{(i)})}$ 可以看做随机变量为 $Q_i(z^{(i)})$ 概率分布函数为 $\frac{p(x^{(i)},z^{(i)};\theta)}{Q_{i}(z^{(i)})}$ 的期望，即为：
$\begin{aligned} \sum_{z^{(i)}} Q_{i} (z^{(i)}) \frac{p (x^{(i)}, z^{(i)}; θ)}{Q_{i} (z^{(i)})} = E (\frac{p (x^{(i)}, z^{(i)}; θ)}{Q_{i} (z^{(i)})}) \end{aligned}$ $\begin{aligned} \underset{z^{(i)}}{\sum}Q_{i}(z^{(i)})\frac{p(x^{(i)},z^{(i)};\theta)}{Q_{i}(z^{(i)})}=E(\frac{p(x^{(i)},z^{(i)};\theta)}{Q_{i}(z^{(i)})}) \end{aligned}$
由Jensen不等式，且 $f(x)=log\; x,f''(x)=-\frac{1}{x^{2}} <0$ ，所以：
$\begin{aligned} f ({\underset{}{E}}_{z^{(i)} \sim Q_{i}} [\frac{p (x^{(i)}, z^{(i)}; θ)}{Q_{i} (z^{(i)})}]) \geq {\underset{}{E}}_{z^{(i)} \sim Q_{i}} [f (\frac{p (x^{(i)}, z^{(i)}; θ)}{Q_{i} (z^{(i)})})] \end{aligned}$ $\begin{aligned} f(\underset{}{E}_{z^{(i)}\sim Q_{i}}[\frac{p(x^{(i)},z^{(i)};\theta)}{Q_{i}(z^{(i)})}])\ge \underset{}{E}_{z^{(i)}\sim Q_{i}}[f(\frac{p(x^{(i)},z^{(i)};\theta)}{Q_{i}(z^{(i)})})] \end{aligned}$

所以参数 $\theta$ 的对数似然性就有了一个下界，我们回想在EM算法的形式化过程中的不断推进得到的下界不断上升的过程，在这里我们也希望得到一个更加紧密的下界，也就是使等号成立的情况。
根据Jensen不等式，所以有：

\begin{aligned} \frac{p (x^{(i)}, z^{(i)}; θ)}{Q_{i} (z^{(i)})} = c (c 为 常 数) \end{aligned}

$\begin{aligned}\frac{p(x^{(i)},z^{(i)};\theta)}{Q_{i}(z^{(i)})} =c \;\;\;(c为常数) \end{aligned}$
所以：

\begin{aligned} Q_{i} (z^{(i)}) = c * p (x^{(i)}, z^{(i)}; θ) (c 为 常 数) \end{aligned}

$\begin{aligned}{Q_{i}(z^{(i)})} =c*{p(x^{(i)},z^{(i)};\theta)} \;\;\;(c为常数) \end{aligned}$
因为

\sum_{Z} Q_{i} (z) = 1, Q_{i} (z) \geq 0

$\sum_{Z}Q_{i}(z)=1,Q_{i}(z)\ge0$ ，所以：

\begin{aligned} \sum_{Z} Q_{i} (z^{(i)}) = \sum_{Z} c * p (x^{(i)}, z^{(i)}; θ) = 1 (c 为 常 数) \end{aligned}

$\begin{aligned}\sum_{Z}{Q_{i}(z^{(i)})} =\sum_{Z}c*{p(x^{(i)},z^{(i)};\theta)}=1 \;\;\;(c为常数) \end{aligned}$
所以：

\begin{aligned} c = \frac{1}{\sum_{Z} p (x^{(i)}, z^{(i)}; θ)} (c 为 常 数) \end{aligned}

$\begin{aligned}c=\frac{1}{\sum_{Z}{p(x^{(i)},z^{(i)};\theta)} }\;\;\;(c为常数) \end{aligned}$
所以：

\begin{aligned} Q_{i} (z^{(i)}) & = \frac{p (x^{(i)}, z^{(i)}; θ)}{\sum_{z} p (x^{(i)}, z; θ)} \\ = \frac{p (x^{(i)}, z^{(i)}; θ)}{p (x^{(i)}; θ)} \\ = p (z^{(i)} | x^{(i)}; θ) \end{aligned}

$\begin{aligned}Q_{i}(z^{(i)})&=\frac{p(x^{(i)},z^{(i)};\theta)}{\sum_{z}{p(x^{(i)},z;\theta)}}\\&=\frac{p(x^{(i)},z^{(i)};\theta)}{{p(x^{(i)};\theta)}}\\&=p(z^{(i)}|x^{(i)};\theta) \end{aligned}$

EM算法

EM算法主要有两个步骤，EM算法的具体内容如下：、
Repeat until convergence{

(E-step) for each i, set
$\begin{aligned} Q_{i} (z^{(i)}) := p (z^{(i)} | x^{(i)}; θ) \end{aligned}$ $\begin{aligned}Q_{i}(z^{(i)}):=p(z^{(i)}|x^{(i)};\theta) \end{aligned}$
(M-step) set
$\begin{aligned} θ := arg max_{θ} \sum_{i} \sum_{z^{(i)}} Q_{i} (z^{(i)}) l o g \frac{p (x^{(i)}, z^{(i)}; θ)}{Q_{i} (z^{(i)})} \end{aligned}$ $\begin{aligned}\theta:=\text{arg}\;\;\underset{\theta}{\text{max}}\;\;\underset{i}{\sum}\underset{z^{(i)}}{\sum}Q_{i}(z^{(i)})log\frac{p(x^{(i)},z^{(i)};\theta)}{Q_{i}(z^{(i)})} \end{aligned}$

｝

收敛性证明

我们可以定义一个优化目标

\begin{aligned} J (Q, θ) = \sum_{i} \sum_{z^{(i)}} Q_{i} (z^{(i)}) l o g \frac{p (x^{(i)}, z^{(i)}; θ)}{Q_{i} (z^{(i)})} \end{aligned}

$\begin{aligned}J(Q,\theta)=\underset{i}{\sum}\underset{z^{(i)}}{\sum}Q_{i}(z^{(i)})log\frac{p(x^{(i)},z^{(i)};\theta)}{Q_{i}(z^{(i)})}\end{aligned}$
使用Jensen不等式，我们可以推导出：

\begin{aligned} l (θ) \geq J (Q, θ) \end{aligned}

$\begin{aligned}l(\theta)\geq J(Q,\theta)\end{aligned}$
回顾前面所学的知识，EM 可以看作是函数 J 的坐标上升法，E步固定θ优化Q，M 步固定Q优化θ。再利用相关知识便可以证明。

Andrew Ng机器学习课程笔记（十三）之无监督学习之EM算法