周一到周五,每天一篇,北京时间早上7点准时更新~
Curves(曲线)
If moving everything along a straight line between two points is all we wanted to do, then this would be enough. However, in the real world, objects move in smooth curves and accelerate and decelerate smoothly. A curve can be represented by three or more control points. For most curves, there are more than three control points, two of which form the endpoints; the others define the shape of the curve. Consider the simple curve shown in Figure 4.14
如果沿着一条直线运动就能满足我们的所有需求,那么线性插值就足够了,然而,实际上,物体更多的是沿着曲线运动,慢慢的加速和减速。三个或者三个以上的点可以表达一个曲线,大部分曲线有三个以上的控制点。 其中两个点用来定义边界,其他的点用来定义曲线的形状,图4.14展示了一个简单的曲线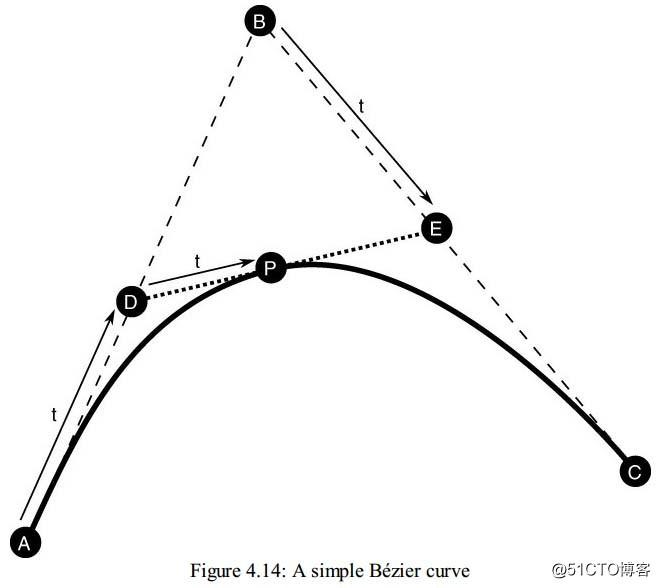
The curve shown in Figure 4.14 has three control points, A, B, and C. A and C are theendpoints of the curve and B defines the shape of the curve. If we join points A and B with one line and points B and C together with another line, then we can interpolate along the two lines using a simple linear interpolation to find a new pair of points, D and E. Now, given these two points, we can join them with yet another line and interpolate along it to find a new point, P. As we vary our interpolation parameter, t, point P will move in a smooth curved path from A to D. Expressed mathematically, this is
图4.14中的曲线有3个控制点,其中A和C是端点,B控制着曲线的形状。如果我们将AB和BC连起来,我们就可以沿着这两条线段进行线性插值,找到类似于D、E这样的一对一对的点。 连接D、E两点又可以得到一条新的线段,插值这条线又会得到新的点p。当我们去让t变化,就可以得到p点从A到D平滑运动,计算公式如下: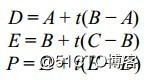
Substituting for D and E and doing a little crunching, we come up with the following:(同样的对于D、E之间的插值,我们有如下式子:)
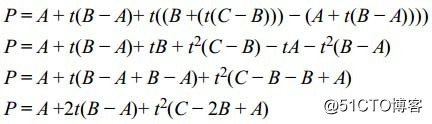
You should recognize this as a quadratic equation in t. The curve that it describes is known as a quadratic Bézier curve(你会发现,这个插值实际上就是二阶的贝塞尔曲线). We can actually implement this very easily in GLSL using the mix function, as all we’re doing is linearly interpolating (mixing) the results of two previous interpolations(我们在GLSL里面很容易去实现这一插值)
vec4 quadratic_bezier(vec4 A, vec4 B, vec4 C, float t)
{
vec4 D = mix(A, B, t); // D = A + t(B - A)
vec4 E = mix(B, C, t); // E = B + t(C - B)
vec4 P = mix(D, E, t); // P = D + t(E - D)
return P;
}
By adding a fourth control point as shown in Figure 4.15, we can increase the order by 1 and produce a cubic Bézier curve.
当我们添加第四个控制点后,这个插值又变成了三次方的贝塞尔曲线了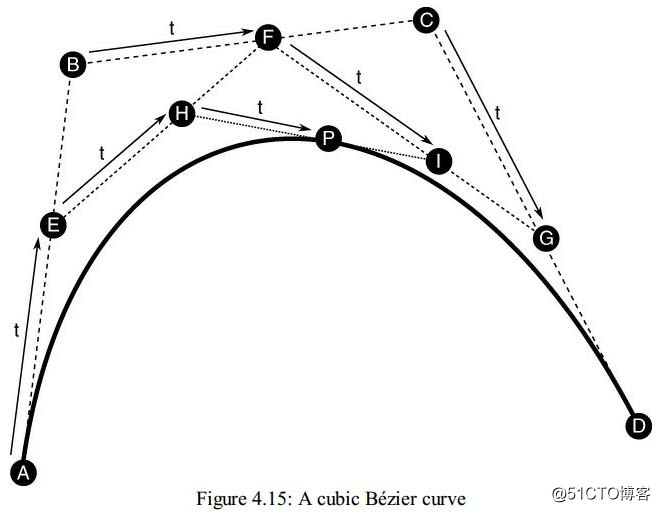
We now have four control points, A, B, C, and D. The process for constructing the curve is similar to that for the quadratic Bézier curve. We form a first line from A to B, a second line from B to C, and a third line from C to D. Interpolating along each of the three lines gives rise to three new points, E, F, and G. Using these three points, we form two more lines, one from E to F and another from F to G, interpolating along which gives rise to points H and I, between which we can interpolate to find our final point, P. Therefore, we have
现在我们有四个控制点了,构建曲线的方法跟三个控制点构建曲线的方法类似。我们首先连接AB、BC、CD,然后分别对他们插值,得到新的点E、F、G。然后用这仨点做出新的两条线EF、FG, 然后继续对EF、FG插值得到H、I点,然后我们对HI进行插值,得到了p点,这样一来我们有下面的公式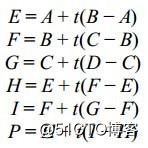
If you think these equations look familiar, you’re right: Our points E, F, and G form a quadratic Bézier curve that we use to interpolate to our final point P. If we were to substitute the equations for E, F, and G into the equations for H and I, then substitute those into the equation for P, and crunch through the expansions, we would be left with a cubic equation with terms in t—hence the name cubic Bézier curve. Again, we can implement this simply and efficiently in terms of linear interpolations in GLSL using the mix function:
如果你觉得这个等式非常相似,那么你的直觉是正确的,我们E、F、G组成了的二次方的贝塞尔曲线去插值p点的时候,如果把E、F、G求得H、I,那么就可以得到P,如此这般,最后我们就会得到 由因子t影响的插值公式,下面给出了GLSL里面的插值实现算法
vec4 cubic_bezier(vec4 A, vec4 B, vec4 C, vec4 D, float t)
{
vec4 E = mix(A, B, t); // E = A + t(B - A)
vec4 F = mix(B, C, t); // F = B + t(C - B)
vec4 G = mix(C, D, t); // G = C + t(D – C)
vec4 H = mix(E, F, t); // H = E + t(F - E)
vec4 I = mix(F, G, t); // I = F + t(G - F)
vec4 P = mix(H, I, t); // P = H + t(I - H)
return P;
}
Just as the structure of the equations for a cubic Bézier curve “includes” the equations for a quadratic curve, so, too, does the code to implement them. In fact, we can layer these curves on top of each other, using the code for one to build the next
正如三次方与二次方的贝塞尔曲线的关系那样,是包含关系,实际上,咱们的代码也是这样的包含关系。如下所示:
vec4 cubic_bezier(vec4 A, vec4 B, vec4 C, vec4 D, float t)
{
vec4 E = mix(A, B, t); // E = A + t(B - A)
vec4 F = mix(B, C, t); // F = B + t(C - B)
vec4 G = mix(C, D, t); // G = C + t(D - C)
return quadratic_bezier(E, F, G, t);
}
Now that we see this pattern, we can take it further and produce even higher-order curves. For example, a quintic Bézier curve (one with five control points) can be implemented as
类似的,我们可以得到更高阶的曲线的推导公式,长相如下这般
vec4 quintic_bezier(vec4 A, vec4 B, vec4 C, vec4 D, vec4 E, float t)
{
vec4 F = mix(A, B, t); // F = A + t(B - A)
vec4 G = mix(B, C, t); // G = B + t(C - B)
vec4 H = mix(C, D, t); // H = C + t(D - C)
vec4 I = mix(D, E, t); // I = D + t(E - D)
return cubic_bezier(F, G, H, I, t);
}
This layering could theoretically be applied over and over for any number of control points. However, in practice, curves with more than four control points are not commonly used. Rather, we use splines.
这种形势的曲线实际上可以一层层的嵌套下去,但是在现实中,我们很少使用有4个控制点以上的贝塞尔曲线,如果控制点比较多的使用我们使用样条曲线
本日的翻译就到这里,明天见,拜拜~~
第一时间获取最新桥段,请关注东汉书院以及图形之心公众号
东汉书院,等你来玩哦