首先我们来看一下巴什博弈。

例题1：两个聪明绝顶的人一块报数，每人每次报最少1个，最多报4个，看谁先报到30谁赢，A先报数。（最基础）

我们从B的角度观察这个游戏，我们发现无论A报出几个数字（比如x），B只要报出（5-x）个数，就可以保证自己必胜。

（没什么思考难度）

例题2：有n个物品放置一堆，两个聪明绝顶的人轮流从中取物，规定每次至少取1个，最多取m个，最后取光者得胜。

引入博弈论的部分我就不加赘述了，直接（热度）分析。

结论：找到这么一个整数k和r，使n=k*（m+1）+r，若r==0先手必败，r！=0先手必胜。

（雾？）

（思考—ing）

证明：

　　进行分类讨论：

当n<=m时，先手必胜。（废话）
当n=m+1时，先手必败。（还是废话）
当n=k*(m+1)时，先手必败（k次讨论2循环）
当n=k*(m+1)+x (0<x<m+1)时，先手必胜（通过第一次操作回到讨论3，此时他为后手，必胜）。

　　由此，我们综上所述：

当n=k*(m+1) (k>=1)时先手必败；
否则先手必胜。

在看完巴什游戏之后，我们可以再在雾中欣赏学习一下威佐夫博弈。

定义：

　　有两堆若干物品，两个聪明绝顶的人轮流从中：1.任选一堆取若干个物品；

　　　　　　　　　　　　　　　　　　　　　　 2.同时从两堆取同样多的物品；

　　　　　　　　　　　　　　　　　　　　　　　3.每次至少取一个，无上限。

　　　　　　　　最后去光的人获胜。

结论：

若两堆物品的初始值为（x，y），且x<y，则另z=y-x；

记w=（int）[（（sqrt（5）+1）/2）*z ]；

若w=x，则先手必败，否则先手必胜。

 1 #include<bits/stdc++.h>
 2 using namespace std;
 3 #define ll long long
 4 ll a,b,t,ret,pd;
 5 int main(){
 6     cin>>a>>b;
 7     if(b>a) t=a,a=b,b=t;
 8     ret=a-b;
 9     pd=(ll)((sqrt(5.0)+1.0)/2.0*ret);
10     if(pd==b) cout<<0;
11     else cout<<1;
12     return 0;
13 }

View Code

关于威佐夫博弈的证明：

我们先找到前几组P-局面：（0，0），（1，2），（3，5），（4，7），（6，10），……

诶？（震惊）有几个规律！！！

1.他不重复地取遍了所有数。(emmmmmm)

2.对于第k个P-局面（x，y），x为前 0 到 k-1 个P-局面中没有出现的最小自然数，而y=x+k;

此时我们要引入一个很重要的数学定理——贝蒂定理

定理内容：设a、b是正无理数且 1/a +1/b =1。记A={ [na] | n为任意的正整数}，B={ [nb] | n 为任意的正整数}，([x]'指的是取x的整数部分)则A与B是Z+的一个划分。

证明（分三部分证明）：

1.对于所有整数，最多只会在P（Q）中出现一次。（即规律1）

由于 1/a +1/b =1，得到a，b均大于1，所以（na/nb）向下取整，不会有重复。

2.把<A与B是Z+的一个划分>这句话拆成：

A与B的交集为空。
A与B的并集为自然数。

下面我们证明1：

反证法证明若存在一个k满足它既属于A又属于B；

那么必然有正整数m,n,满足：

化化化->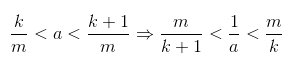

同理：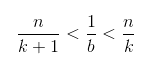

两式求和：可得 (m+n)/(k+1) < 1 < (m+n)/k

再化一步->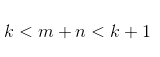

很明显是不合法的，证毕。

下面我们证明2

同上用反证法证明。

若存在一个k满足它既不属于A与B的并集也不属于N（自然数）的补集。

那么也必然有m,n,满足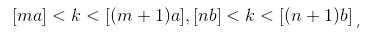

这不可能，证毕。

（注：以上证明转载自Michael_GLF，在此鸣谢。）

链接在此：https://blog.csdn.net/g21glf/article/details/87888285；

根据betty定理，对于1/A+1/B=1，必有
Ua={trunc(A*k),k为正整数}
Ub={trunc(B*k),k为正整数}
Ua与Ub的并集构成正整数集且Ua于Ub不相交
所以设某个必败态的第一项为trunc(A*k)，第二项为trunc(A*k+k)=trunc((A+1)*k)
则1/A+1/(A+1)=1，求得A为(sqrt(5)+1)/2;

博弈论之——巴什博弈、威佐夫博弈。