LeetCode 120.三角形最小路径和

这道题目是给定一个三角形的数组，找到自顶向下的的一条路径，使得路径上的元素之和最小，首先我们来看一下这道题的题目：
triangle
首先我们拿到这个题目，我们会想到递归的方法，因为我们每次向下只能选择相邻的元素，那么我们递归的方程可以写成：

triangle(i,j){
	triangle(i, j + 1);
	triangle(i + 1, j + 1)
}

我们用这种递归的方法可以遍历所有的路径，我们可以将每一条路径的元素之和记录下来然后选取最小的那个，就是这道题目的解，这种解法的时间复杂度为 $O(2^n)$ 。这显然不是最佳的解法，接下来我们可以考虑贪心算法，每次选取和自己相邻的最小的那个元素，仔细一想，这种算法显然无法满足全局的最优解，容易陷入局部的最优解，那么贪心算法是不可取的。最后我们可以想到运用动态规划的算法来分析这道题目：首先我们自底向上来考虑，我们将第 $i,j$ 个元素的最优解记为 $DP(i,j)$ ，那么 $DP(i,j)$ 就等于与 $i,j$ 相邻位置的 $DP$ 函数加上 $i, j$ 位置上的元素本身，所以整个动态规划的递推方程可以写成： $DP(i, j)=min(DP(i,j+1),DP(i+1,j+1))+triangle(i,j)$
有了这个动态规划方程之后，我们自底向上递推上去，最终最顶上的 $DP(0,0)$ 就是我们要求的结果。我们来看一个具体的例子，下面是例子中给的一个三角形：

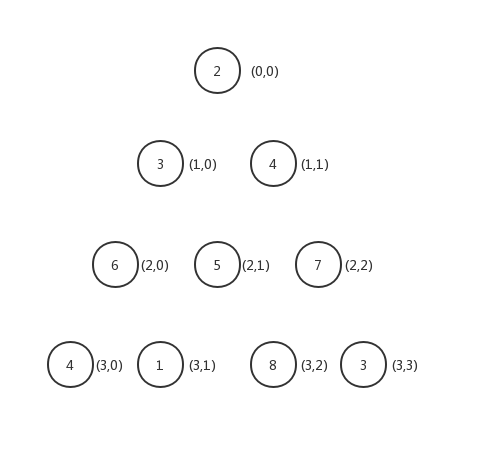
我们由最下面一层开始进行动态规划，可以求得最下面一层位置的DP函数值：
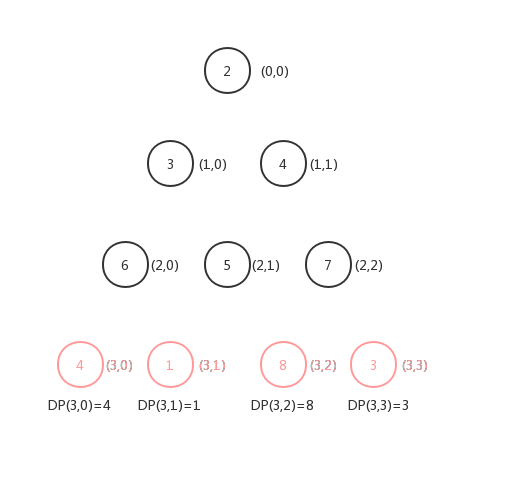
triangle2
可以求得，最下面一层的 $DP$ 值就是元素本身，那么我们可以继续向上 $DP$ :

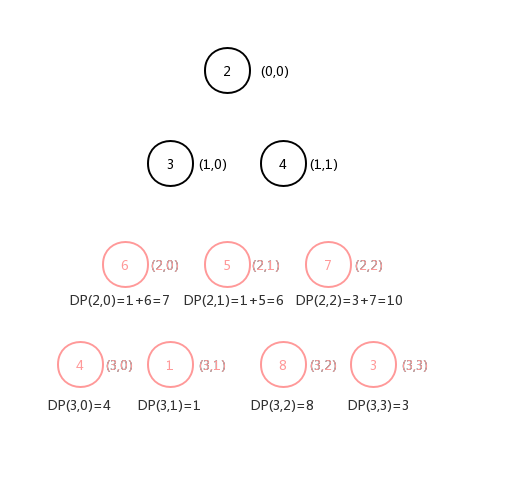
可以看到倒数第二层，每一层的 $DP$ 函数值等于与自己相邻最小元素的值加上自己本身的值，同理我们可以继续往上 $DP$ :

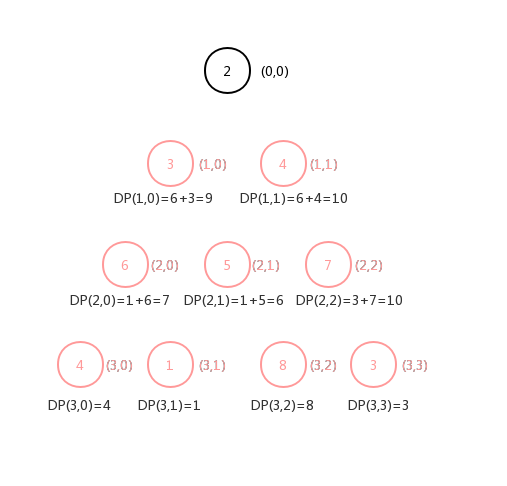
直到第二层，最终我们 $DP$ 到 $(0,0)$ 这个位置就可以求出我们的解了：
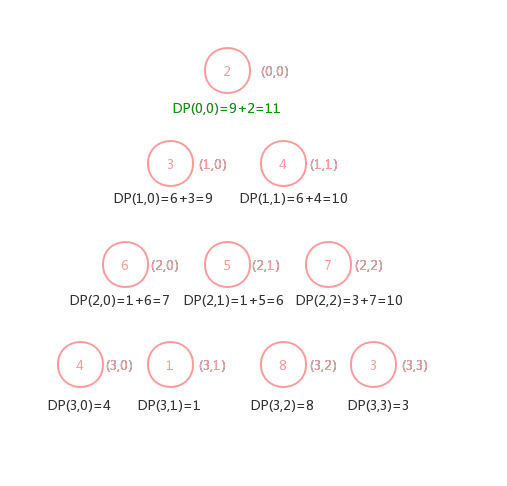
triangle
最终我们就可以求出本题目的答案 $DP(0,0)=11$ ，所以整个算法的流程应该可以说是非常清晰了，整个算法的复杂度为 $O(ij)$ ，下面来看代码：

java:

class Solution {
    public int minimumTotal(List<List<Integer>> triangle) {
        if(triangle.size() == 0 || triangle.get(0).size() == 0)
            return 0;
        for(int i = triangle.size() - 2; i >= 0; --i){
            for(int j = triangle.get(i).size() - 1; j >= 0; --j){
                int min = Math.min(triangle.get(i + 1).get(j), triangle.get(i + 1).get(j + 1));
                min += triangle.get(i).get(j);
                triangle.get(i).set(j, min);             
            }
        }
        return triangle.get(0).get(0);
    }
}

python:

class Solution(object):
    def minimumTotal(self, triangle):
        """
        :type triangle: List[List[int]]
        :rtype: int
        """
        if not triangle:
            return 0
        res = triangle[-1]
        for i in range(len(triangle) - 2, -1, -1):
            for j in range(len(triangle[i])):
                res[j] = min(res[j], res[j+1])+ triangle[i][j]
        return res[0]

这道题目是 $DP$ 动态规划的一个非常经典的题目，希望大家可以通过此博文可以很透彻地理解动态规划的思想，谢谢。