Dimensionality Reduction(降维)

前言

在前面，我们给大家介绍了一种无监督学习的算法K-means，是来解决聚类问题的，在这一章我将给大家介绍另一种无监督学习算法，是用来解决降维问题的，叫做Principal Component Analysis(主成分分析法)。

最后，如果有地方理解不对的，希望大家不吝赐教，谢谢！

第十二章 Dimensionality Reduction(降维)

12.1 数据压缩

我们在介绍降维之前，首先要问一个问题，为什么要进行降维？有时候我们在处理一些数据时，会出现这样的情况，比如我们要测量一个物体，我们用厘米作为一个特征x1，而又用英尺作为一个特征x2，得到两组数据，显然这是冗余的，两者所表达的是同一个意思而已，所以我们以两者为变量，会得到他们的数据成一个线性关系。有可能你会问，我们在选择特征作为变量时，怎么会犯这种问题，但是当你在做一个比较大的项目时，你分给几个人去收集数据，难免会遇到特征类似的数据，这个时候就会造成冗余，我们就需要对数据进行降维，比如刚刚那个2D的问题，我们就可以对此降维成1D的，如图1所示，我们根据数据做出一条直线，使得数据到直线的距离和最小，我们把这条直线的方向做为一个新空间的坐标轴，即1D空间的坐标轴，可以有两个方向，然后再把每个数据映射到这条新的坐标轴上，这个时候就把2D降维成了1D。

图1 2D降维成1D

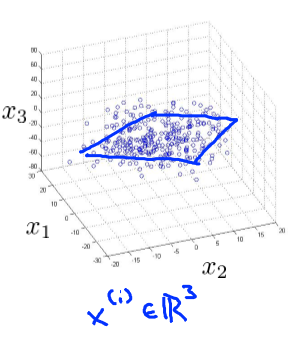
同样的，对于一个3D问题，我们也同样可以通过降维成2D的，如图2所示，我们有一组3D的数据集，可以发现，这些数据大致在一个平面上，所以我们可以选取一个2D的平面，使得每个数据到这个平面的距离和最小，如图3所示，对这个平面的两个方向选为z1和z2，即新的2D空间的横纵坐标轴，然后把每个数据映射到这个平面上，这个时候，我们的新的2D空间的数据就有了，如图4所示，这个时候新的数据 $z^{(i)}$ 就是2D的了，即 $z\in R^{2}$ ， $z^{(i)}=\begin{bmatrix} z_{1}^{(i)}\\ z_{2}^{(i)} \end{bmatrix}$ 。

图2 3D的数据集

图3 选择一个2D平面

图4 新的2D数据集

对数据进行降维后，我们在存储时明显可以减少原本占用的内存，而且在算法执行时也会更快。

12.2 数据的可视化

在前面给大家介绍的数据压缩只是我们进行降维的好处之一，还有一个好处就是数据的可视化。很多实际问题，我们都知道一组数据有很多的特征，比如分析各个国家的GDP、人民幸福度等等，我们对于每个国家就会有得到很多的特征，如图5所示，对于这个输入X，我们就可能会有 $x\in R^{50}$ ，这个时候如果我们想把这些数据画在一张图上，显然是不可能的，我们在实际中最多可以表示出3D的空间，再更多维的就不行了，所以如果我们想让数据可视化，则需要对数据进行降维，如图6所示，我们最终降维的结果，我们会发现如果z1代表国家的大小，z2代表国家的GDP，则USA可能是图6中那一点，我们就会很清楚的明白一些特征之间的关系。z1和z2可以代表不同的特征，我们会得到不同的结果，但这样我们对整个特征和数据之间的关系就有了一个可视化的感受。

图5 关于各国一些情况调查表

图6 数据降维成2D的结果

12.3 Principal Component Analysis problem formulation(主成分分析问题的公式)

在前面我们给大家介绍了为什么要进行降维，一个是对数据进行压缩，节约内存和是算法运行更快，另一个是让高维数据可视化。在这一节，我将给大家介绍怎样来实现数据的降维，我们所用到的是Principal Component Analysis(PCA)，首先我们来介绍下PCA到底在做一件什么样的事，对于前面一个2D的问题降维到1D，如图7所示，首先我们会选取一条直线，使得每个数据到直线的距离和最小，对于这条直线的方向有两种，我们用 $u^{(1)}$ 和- $u^{(1)}$ 来表示。对于一个n维的数据降维到K维，同样的，我们选取K个向量 $u^{(1)},u^{(2)},...,u^{(k)}$ 构成一个新的K维空间，使得原始n维空间的数据到K维空间的距离和最小，然后再把n维的数据映射到K维中。

图7 PCA实现2D降维到1D

在这里，大家可能会有个问题，就是这个降维的过程貌似和线性拟合有些相似，他们是一样的吗？答案：肯定不是的，我们对二者进行对比，如图8所示，线性拟合中有一个特殊的变量就是输出变量y，在这里我们所求的距离和是每一个数据预测输出的结果和实际结果的距离值，在图中可以看出是每一个竖着的距离和，而我们的降维的对象是平等的输入变量x，所求的距离和是数据到直线的垂直距离和，两者不能混为一谈。

图8 线性拟合和降维的比较

12.4 PCA算法的实现过程

在前面只是给大家一个比较直观的感受来了解PCA是怎样实现的，现在将给大家详细地介绍这个算法一步步的数学实现过程。对于训练集 $x^{(1)},x^{(2)},...,x^{(m)}$ ，我们第一步要做的是特征的放缩，在前面预测房子的价格问题时，我们也有给大家讲到这个，在这里就不过多地解释它的含义了，我们直接给出式子： $\mu _{j}=\frac{1}{m}\sum_{i=1}^{m}x_{j}^{(i)}$ ，而新的 $x_{j}^{(i)}$ 则是 $x_{j}^{(i)}-\mu _{j}$ ，有时候我们会这样做把 $\frac{x_{j}^{(i)}-\mu _{j}}{s_{j}}$ 作为新的 $x_{j}^{(i)}$ ，不管怎样做，我们的目的就是让每个数据在同一个范围类。然后就是进行PCA算法了，关于算法本身的原理，这里就不进行讲解了，如果想了解可以自行查找资料，这个原理有点复杂，下面只给大家介绍实现的过程。首先我们计算 $\Sigma =\frac{1}{m}\sum_{i=1}^{m}(x^{(i)})(x^{(i)})^{\top }$ ，这是得到一个协方差矩阵，注意这里最终得到的矩阵是n*n的，还有就是 $\Sigma$ 注意和求和符号进行区别，这是大写的Sigma，接下来我们用一个函数svd即可得到以上我们想要的各个矩阵，svd用法是这样的：[U,S,V]=svd(Sigma);我们得到的U是n*n的，而如果想得到一个K维的结果，那么我们只需要选择U的前K列即可，而我们所需要的n维中的数据x对应到K维中的z，即z=X*U(:,1:K)，注意x是m*n的，而U是n*K的，所以最后z是m*k的，即我们的数据从n维降维到了K维。

12.5 从压缩的数据中重建原始的数据

在前面，我们一直在讲如何对一个高维的数据降维的问题，那么当我们拿到是降维后的数据，该怎样恢复得到原始的数据了？首先要说明一点，我们想得到和原先一模一样的数据是不可能的，我们得到的只是原始数据的一个接近值。如图9所示，图中左边就是我们在通过PCA从一个2D降维到1D，而右边就是根据降维后的数据重建原始数据，我们得到的只是一个接近值，我们的做法就是： $x_{approx}=z*U(:,1:K)'$ ，注意z是m*K的，而U是n*K的，所以 $x_{approx}$ 是m*n的，也正好符合原始数据x的维数。

图9 降维和对数据的重建

12.6 选择主成分的数量

选择主成分的数量说白了就是选择K，我们只知道要降维，那么到底降维到几维就满足我们的要求了，在这里我们给出要求。首先向大家给出平均平方误差： $\frac{1}{m}\sum_{i=1}^{m}\left \| x^{(i)}-x_{approx}^{(i)} \right \|^2$ ，还有数据总的variation： $\frac{1}{m}\sum_{i=1}^{m}\left \| x^{(i)}\right \|^2$ ，我们就是要选择一个K使得 $\frac{\frac{1}{m}\sum_{i=1}^{m}\left \| x^{(i)}-x_{approx}^{(i)} \right \|^2}{\frac{1}{m}\sum_{i=1}^{m}\left \| x^{(i)}\right \|^2}\leq 0.01$ ，这里不一定是0.01，可以是其他的值，如果是0.01就表示我们会得到99%的方差是保留的。所以可以根据情况看我们需要让其值小于等于多少。那么在算法中该怎样做了？首先我们当然希望K越小越好，所以我们会对K从1开始递增，每次通过计算 $\frac{\frac{1}{m}\sum_{i=1}^{m}\left \| x^{(i)}-x_{approx}^{(i)} \right \|^2}{\frac{1}{m}\sum_{i=1}^{m}\left \| x^{(i)}\right \|^2}$ ，判断其值是否<=0.01，即作为结束条件找到合适的K值。原理是这样的没错，但在前面我们通过[U,S,V]=svd(Sigma)，得到了一个S矩阵，这是一个n*n的矩阵，是一个对角矩阵，就是指只有对角线上有值，其他地方的值都为0，则 $\frac{\frac{1}{m}\sum_{i=1}^{m}\left \| x^{(i)}-x_{approx}^{(i)} \right \|^2}{\frac{1}{m}\sum_{i=1}^{m}\left \| x^{(i)}\right \|^2}$ 可以表示成 $1-\frac{\sum_{i=1}^{k}S_{ii}}{\sum_{i=1}^{n}S_{ii}}$ ，注意这里的 $S_{ii}$ 即是S的对角线上的元素，所以我们的判断条件就变成了 $1-\frac{\sum_{i=1}^{k}S_{ii}}{\sum_{i=1}^{n}S_{ii}}\leq 0.01$ ，即 $\frac{\sum_{i=1}^{k}S_{ii}}{\sum_{i=1}^{n}S_{ii}}\geq 0.99$ ，这样我们就可以利用S来计算了。

12.7 关于PCA应用的一些建议

首先我们对于一组训练集的数据是否一定要做PCA？当拿到一组训练集时，我们首先做的是就根据原始数据进行训练，看我们的算法实现是否够快，如果过程比较理想就没必要使用PCA了，毕竟PCA的过程还是很需要计算量的，也比较花时间的。如果我们确定了需要进行PCA，那么我们需要的是对训练集的数据进行PCA，不是交叉聚数据也不是测试数据。还有就是在对数据进行压缩时，我们需要根据想保留多少的方差来选择合适的K值，还有就是需要对数据进行可视化处理时，则K的选择可以是2或者3。最后一个问题就是在对数据进行PCA时，我们一个直观的感受就是对数据的特征进行减少了，那么是否可以用PCA来解决我们前面所说的过度拟合问题了？答案不是不可以，而是没有我们前面所用的正则化更加好，所以不建议大家使用PCA来解决过度拟合的问题，而是用我们前面的正则化方法。

Dimensionality Reduction(降维)

前言

猜你喜欢