1. 背景

线性回归，就是能够用一条线较为精确地描述数据之间的关系。这样当出现新的数据的时候，就能够预测出一个简单的值。线性回归中最常见的就是房价的问题：已知房子的特征（面积、 $\cdots$ ）和房价，构建一个模型，预测其它房子的房价。如图
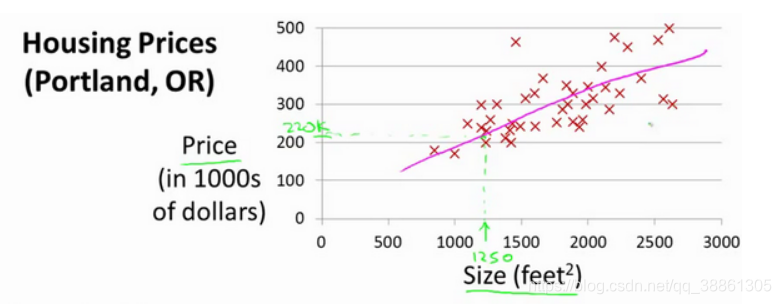
在这里插入图片描述

2. 线性回归的模型函数和损失函数

线性回归遇到的问题一般是这样的。我们有m个样本，每个样本对应于n维特征和一个结果输出，如下：
$(x^{(0)}_1,x^{(0)}_2,\cdots,x^{(0)}_n,y_0), (x^{(1)}_1,x^{(1)}_2,\cdots,x^{(1)}_n,y_1), (x^{(m)}_1,x^{(m)}_2,\cdots,x^{(m)}_n,y_m)$

我们的问题是，对于一个新的 $(x^{(x)}_1,x^{(x)}_2,\cdots,x^{(x)}_n)$ 他所对应的y_x是多少呢？如果这个问题里面的y是连续的，则是一个回归问题，否则是一个分类问题。
对于n维特征的样本数据，如果我们决定使用线性回归，那么对应的模型是这样的：
$h_θ(x_1,x_2,\cdots,x_n)=θ_0+θ_1x_1+\cdots+θ_nx_n$

其中θ_i(i = 1,2… n)为模型参数，x_i (i = 1,2… n)为每个样本的n个特征值。这个表示可以简化，我们增加一个特征x0=1 ，这样 $h_θ(x_0,x_1,...x_n)=∑_{i=0}^nθ_ix_i。$

进一步用矩阵形式表达更加简洁如下：
$h_θ(X)=Xθ$

其中，假设函数h_θ(X)为m x 1的向量,θ为n x 1的向量。X为m x n维的矩阵。m代表样本的个数，n代表样本的特征数。

得到了模型，我们需要求出需要的损失函数，一般线性回归我们用均方误差作为损失函数。损失函数的代数法表示如下：
$J(θ_0,θ_1,\cdots,θn)=∑_{i=0}^m(h_θ(x_0,x_1,\cdots,x_n)−y_i)^2$

进一步用矩阵形式表达损失函数：
$J(θ)=\frac{1}{2}(Xθ−Y)^T(Xθ−Y)$

由于矩阵法表达比较的简洁，后面我们将统一采用矩阵方式表达模型函数和损失函数。

3. 线性回归的算法

对于线性回归的损失函数J(θ)= $\frac{1}{2}$ (Xθ−Y)^T(Xθ−Y)，我们常用的有两种方法来求损失函数最小化时候的θ参数：一种是梯度下降法，一种是最小二乘法。可以点链接到对应的文章链接去阅读。

如果采用梯度下降法，则θ的迭代公式是这样的：
$θ=θ−αX^T(Xθ−Y)$

通过若干次迭代后，我们可以得到最终的θ的结果

如果采用最小二乘法，则θ的结果公式如下：
$θ=(X^TX)^{−1}X^TY$

当然线性回归，还有其他的常用算法，比如牛顿法和拟牛顿法，这里不详细描述。

4. 线性回归的推广：多项式回归

回到我们开始的线性模型， $h_θ(x_1,x_2,\cdots,x_n)=θ_0+θ_1x_1+\cdots+θ_nx_n$ , 如果这里不仅仅是x的一次方，比如增加二次方，那么模型就变成了多项式回归。这里写一个只有两个特征的p次方多项式回归的模型：
$h_θ(x_1,x_2)=θ_0+θ_1x_1+θ_2x_2+θ_3x^2_1+θ_4x_2^2+θ_5x_1x_2$

我们令 $x_0=1,x_1=x_1,x_2=x_2,x_3=x^2_1,x_4=x^2_2,x_5=x_1x_2$ ,这样我们就得到了下式：
$h_θ(x_1,x_2)=θ_0+θ_1x_1+θ_2x_2+θ_3x_3+θ_4x_4+θ_5x_5$

可以发现，我们又重新回到了线性回归，这是一个五元线性回归，可以用线性回归的方法来完成算法。对于每个二元样本特征(x₁,x₂),我们得到一个五元样本特征 $(1,x_1,x_2,x^2_1,x^2_2,x_1x_2)$ ，通过这个改进的五元样本特征，我们重新把不是线性回归的函数变回线性回归。

5. 线性回归的推广：广义线性回归

在上一节的线性回归的推广中，我们对样本特征端做了推广，这里我们对于特征y做推广。比如我们的输出Y不满足和X的线性关系，但是lnY 和X满足线性关系，模型函数如下：
$lnY=Xθ$

这样对与每个样本的输入y，我们用 $lny$ 去对应，从而仍然可以用线性回归的算法去处理这个问题。我们把 $Iny$ 一般化，假设这个函数是单调可微函数 $g(.)$ ,则一般化的广义线性回归形式是：
$g(Y)=Xθ 或者 Y=g^{−1}(Xθ)$

这个函数 $g(.)$ 我们通常称为联系函数。

6. 线性回归的正则化

为了防止模型的过拟合，我们在建立线性模型的时候经常需要加入正则化项。一般有L1正则化和L2正则化。

线性回归的L1正则化通常称为Lasso回归，它和一般线性回归的区别是在损失函数上增加了一个L1正则化的项，L1正则化的项有一个常数系数α来调节损失函数的均方差项和正则化项的权重，具体Lasso回归的损失函数表达式如下：
$J(θ)=\frac{1}{2}(Xθ−Y)^T(Xθ−Y)+α||θ||_1$

其中α为常数系数，需要进行调优。 $||θ||_1$ 为 $L1$ 范数。

Lasso回归可以使得一些特征的系数变小，甚至还是一些绝对值较小的系数直接变为0。增强模型的泛化能力。
Lasso回归的求解办法一般有坐标轴下降法（coordinate descent）和最小角回归法（ Least Angle Regression），由于它们比较复杂，在我的这篇文章单独讲述：线程回归的正则化-Lasso回归小结

线性回归的L2正则化通常称为Ridge回归，它和一般线性回归的区别是在损失函数上增加了一个L2正则化的项，。具体Ridge回归的损失函数表达式如下：
$J(θ)=\frac{1}{2}(Xθ−Y)^T(Xθ−Y)+\frac{1}{2}α||θ||_2$

其中α为常数系数，需要进行调优。 $||θ||_2$ 为 $L2$ 范数。

Ridge回归在不抛弃任何一个特征的情况下，缩小了回归系数，使得模型相对而言比较的稳定，但和Lasso回归比，这会使得模型的特征留的特别多，模型解释性差。
Ridge回归的求解比较简单，一般用最小二乘法。这里给出用最小二乘法的矩阵推导形式，和普通线性回归类似。
令J(θ)的导数为0，得到下式：
$X^T(Xθ−Y)+αθ=0$

整理即可得到最后的θ的结果：
$θ=(X^TX+αE)^{−1}X^TY$

其中E为单位矩阵。

除了上面这两种常见的线性回归正则化，还有一些其他的线性回归正则化算法，区别主要就在于正则化项的不同，和损失函数的优化方式不同，这里就不累述了。

（欢迎转载，转载请注明出处刘建平Pinard：https://www.cnblogs.com/pinard/p/6004041.html）

线性回归原理小结