什么是旋转矩阵
旋转矩阵描述了两个坐标系(SLAM中两个时刻机器人的姿态)之间的相互关系,是SLAM中描述姿态变换的数学工具。为了更深入地理解旋转矩阵及坐标变化,我们简单地以两个原点重合的坐标系来阐释旋转矩阵的含义及其性质。
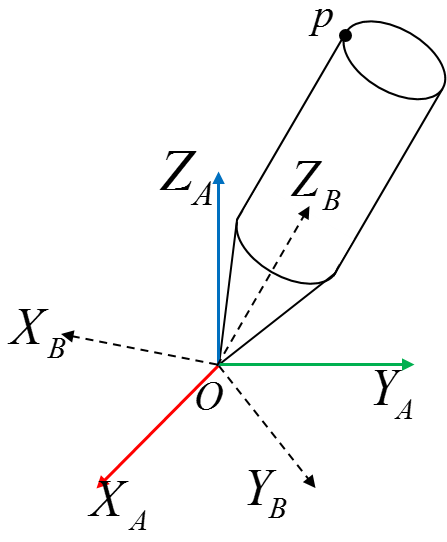
有两个坐标系: \(B\), \(A\),其中 \(B\)为刚体坐标系;两坐标系原点重合,点 \(p\)是刚体上的一点
坐标系B的坐标轴单位向量在坐标系A中的描述为:
\[ \vec X_B=\begin{bmatrix}\alpha_x \\\beta_x \\\gamma_x \\\end{bmatrix},\vec Y_B=\begin{bmatrix}\alpha_y \\\beta_y \\\gamma_y \\\end{bmatrix},\vec Z_B=\begin{bmatrix}\alpha_z \\\beta_z \\\gamma_z \\\end{bmatrix} \]
点\(q\)在坐标系\(B\)和坐标系\(A\)中的坐标分别为 \(p_ B\) ,\(p_A\),如下
\[ p_B=\begin{bmatrix}x_B \\y_B \\z_x \\\end{bmatrix},p_A=\begin{bmatrix}x_A \\y_A \\z_A \\\end{bmatrix} \]
这里有一个重要的理解:坐标是基于某一个坐标系下若干满足一定条件的若干参考向量的度量。点\(p_B\)在坐标系\(B\)中的坐标,其实是基于坐标系\(B\)中三个单位正交基\(e_x=\begin{bmatrix}1&0&0\end{bmatrix}^T\),\(e_y=\begin{bmatrix}0&1&0\end{bmatrix}^T\),\(e_z=\begin{bmatrix}0&0&1\end{bmatrix}^T\),进行的度量,即:
\[ p_B=x_B\cdot\begin{bmatrix}1 \\0 \\0 \\\end{bmatrix}+y_B\cdot\begin{bmatrix}0 \\1 \\0 \\\end{bmatrix}+z_B\cdot\begin{bmatrix}0 \\0 \\1 \\\end{bmatrix} \]
点\(q\)在坐标系\(A\)中的坐标\(p_A\)可以以坐标系\(A\)中三个单位正交向量\(\vec X_B=\begin{bmatrix}\alpha_x&\alpha_y&\alpha_y\end{bmatrix}^T\),\(\vec Y_B=\begin{bmatrix}\beta_y&\beta_y&\beta_y\end{bmatrix}^T\),\(\vec Z_B=\begin{bmatrix}\gamma_z&\gamma_z&\gamma_z\end{bmatrix}^T\)来进行度量,坐标分别为\(x_B\),\(y_B\),\(z_B\),则点\(p\)在坐标系\(A\)中表达如下:
\[ \begin{align} P_A&=x_B\cdot \vec X_B+y_B\cdot \vec Y_B+z_B\cdot \vec Z_B \\ &=x_B\cdot \begin{bmatrix}\alpha_x \\\beta_x \\\gamma_x \\\end{bmatrix}+ y_B\cdot \begin{bmatrix}\alpha_y \\\beta_y \\\gamma_y \\\end{bmatrix}+z_B\cdot \begin{bmatrix}\alpha_z \\\beta_z \\\gamma_z \\\end{bmatrix} \\ &=\begin{bmatrix}\alpha_x & \alpha_y &\alpha_z \\\beta_x & \beta_y & \beta_z \\\gamma_x & \gamma_y & \gamma_z \\\end{bmatrix}\cdot \begin{bmatrix}x_B \\y_B \\z_x \\\end{bmatrix} \\ &=R_B^A \cdot p_B \end{align} \]