**矩阵的行简化阶梯型:**多元方程化简消元求解。
规则:线性消元化简后保证每行首个非零项为1,呈阶梯型。每行首个非零1为主元,其他非零项为自由变量。
出现自有变量时,说明该方程组的个数比未知量(元)少,没法很好的限制解。这样,解就不是一个点(解析解),而是一个方程((一次)线或面 ),或者无解(多个方程表示的线或面不相交)

解的形式为 固定点(2,0,5,0)+向量a和向量b的线性组合。

例1:解为某个点的情况

例2:无解的情况

如下两个方程无解,类似上面无解的情况。
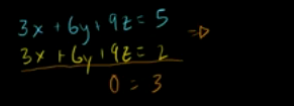
矩阵和向量相互作用
矩阵乘以向量:

矩阵列向量在向量x作用下的线性组合 即向量x决定了矩阵每个列向量的加权值。
也可以理解为矩阵行向量的与向量x点积。
零空间:
Ax = 0; A为已知矩阵,满足Ax=0的所有向量x张成的线性子空间为 零空间。
将矩阵A行简化阶梯型,此时rref(A)x=0 的零空间 等于 Ax=0的零空间。

Ax=0,如果矩阵A各列线性无关,则x为0向量,即方程只有唯一解:0, 即零空间为0
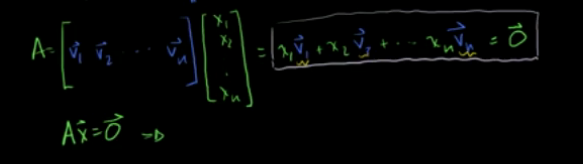
Ax=0,行最简阶梯型如果存在自由变量,则A列向量线性相关。存在自由变量的列都可以用存在主元的列线性表示。
列空间的基为含有主元的列向量组成。
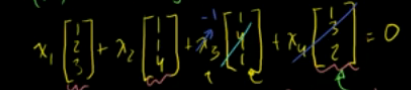
列空间:

则 Ax = b,如果b不在A的列空间,则Ax=b无解。b在A的列空间,则Ax=b至少有一个解。
求一个矩阵的零空间:
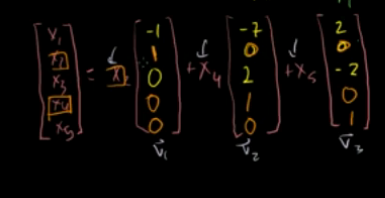
先行简化阶梯型,找到主元,自由变量。

则零空间为v1、v2、v3的线性组合,v1、v2、v3为零空间的一组基。该零空间为3维。
空间维度:
一个子空间的维度等于 该空间一组基底的包含元素的个数(列数)。
行简化阶梯型矩阵的零空间纬度 就是 自由变量的个数。
行简化阶梯型矩阵的列空间纬度 就是 主元的个数。列空间纬度 也叫做 “秩”
函数的深入理解:
一个函数就是一个集合中的元素与另一个集合的关系。(值域 和 定义域)
y=x^2 一维 到 一维 的映射:
x->y的映射。
其中x是R1空间的数(定义域),y也是R1空间的数(值域)。所以这个映射是R1(定义域)->R1(上域)。
二维 到 一维的映射:
函数g将R2点(x1,x2)映射到R1点2.
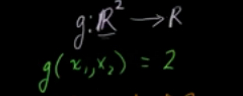
二维 到 三维的映射:
函数h将R2点(x1,x2)映射到R3点(x1+x2,x2-x1,x1x2)
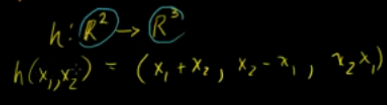
线性变换:
线性变换Transformation 本质就是一个函数,T:Rn -> Rm 该(函数)变换满足必须满足:
如下两条规则用来验证一个变换是否是 线性变换。
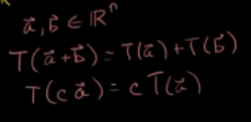
矩阵与向量乘法就是一个线性变换:
定义一个变换:如下
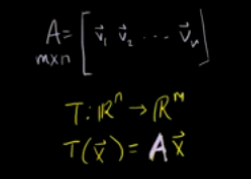
即
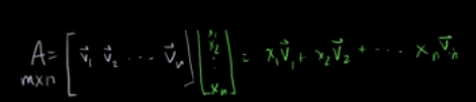
变换T(x)=Bx; 则 T(x1,x2)=(2x1-x2,3x1+4x2) 如下
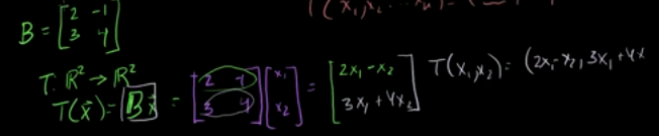
任意线性变换,可以写成矩阵X向量的形式,即 变换可以用矩阵来表达。
已知一个 线性变换:
T(R2 -> R3)
T(x1,x2) = (x1+3x2,5x2-x1,4x1+x2),求该变换的矩阵表达?
根据已知条件,该变换将R2空间向量变换到R3空间向量,那么从R2空间的单位向量入手,将单位向量的每一列执行该变换。
就得到了这个变换矩阵,具体如下:

三条线段的线性变化:


变换后的像:
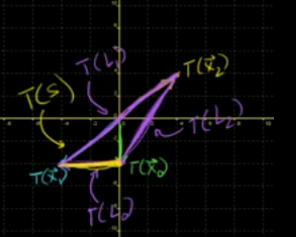
所有的线性变化是将(x1,x2…xn) 变换到矩阵的列空间。
即 所有的变化都是矩阵的列量线的线性组合。

已知变换的像,求原像?
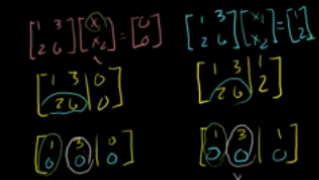
消元后,x1为主元,x2为任意数,令x2=t。得到x1,x2的解,如下:
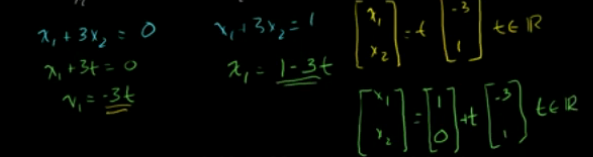
所以,原像为两条直线。
变换的加法和数乘:


变换列题1:翻转变换,求变换矩阵?
将一个三角形沿y轴翻转,并将y值增一倍。则该变换为:T(x,y)=(-x,2y)
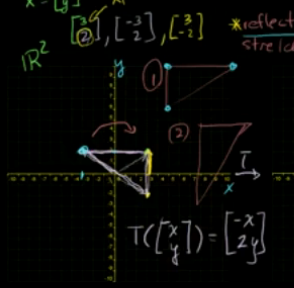
则变换矩阵为:
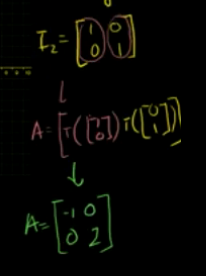
列题2:R2->R2旋转变换?求变换矩阵
将一个向量逆时针旋转一个角度
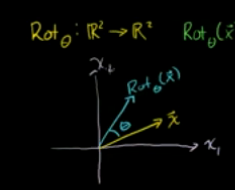
无法根据向量X计算出旋转后的向量的值。
因为是R2->R2的变换,所以先构建一个2X2单位矩阵,从单位矩阵入手。
在单位矩阵上执行这个变换,即单位矩阵的每一列向量执行该变换,即得到该旋转变化的矩阵。

R3->R3的旋转变换:
已知向量在R3中绕X轴旋转

单位向量:
已知向量v,求v同方向的单位向量?
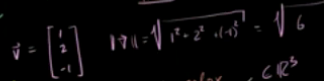
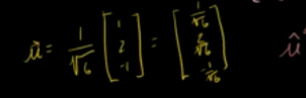
求向量的投影:
(适用于高维)
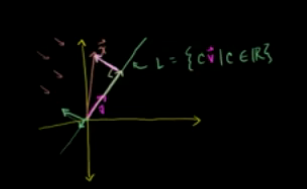
已知向量v,则向量v表示的直线为 L={cv,c属于R}
向量x在L上的投影可以表示为 cv,则垂线段为:x-cv。
所以(x-cv)*v=0,则c=xv/vv
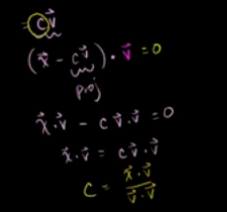
例:
v=(2,1) x=(2,3)

利用单位向量求投影:
已知投影向量为:求出投影矩阵(投影也是线性变化,证明略)
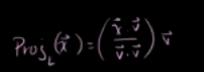
因为:
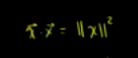
则:
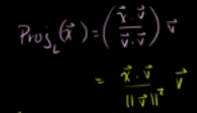
令v等于单位向量,或者求出v的单位向量:
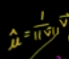
则:
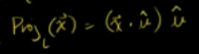
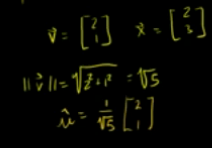
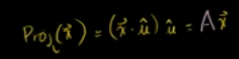
则投影矩阵为:
