写在前面
本篇是B站3Blue1Brown的课程《线性代数的本质》【官方双语/合集】线性代数的本质 - 系列合集_哔哩哔哩_bilibili的自用笔记
向量 线性
- 向量可以理解为一种特定的运动:在空间中朝着某一个方向移动一定距离;
- 向量空间的一组基是张成该空间的一个线性无关向量集。
基是最重要的,二维(i,j),三维(i,j,k)
任何向量都要在一组基下才能确定位置,向量的线性变换本质上是基的变换导致的
例子:
一个向量
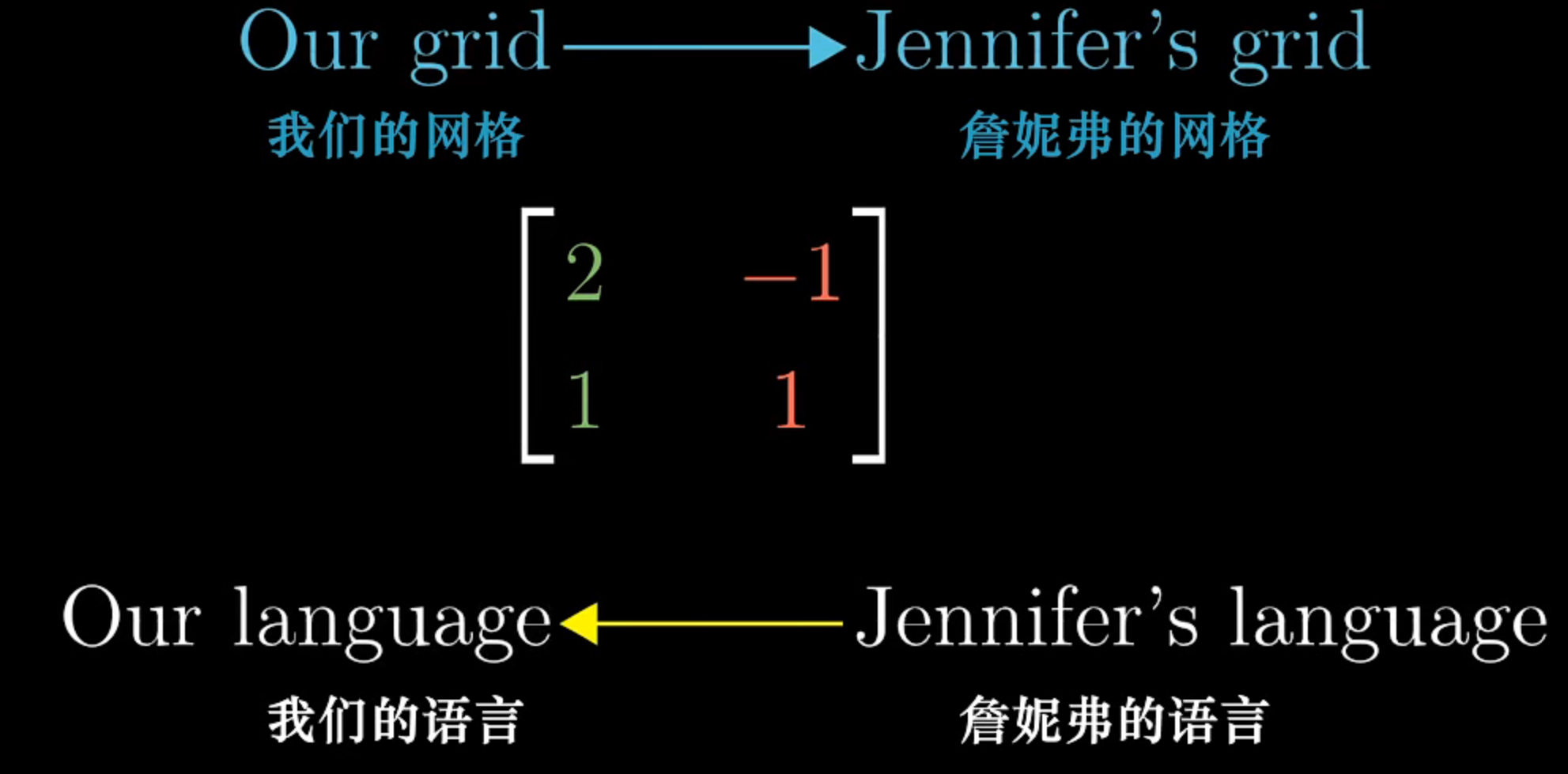
- 正常坐标系i(1,0)j(0,1) 下为 [3 2]T
- 另一个坐标系 b1(1,0) b2(0,1) [(5/3) (1/3)]T
- 如何进行坐标系的翻译?
- 利用基的线性变换
逆变换就叫矩阵的逆

Q:M是一个在标准基下的旋转矩阵,如何作用于基b1b2,使得有同样效果
A:使用基的线性转换A先转化为标准基视角,再进行M操作,最后转回去

- 线性无关:一个向量可以用其他的表示
 如这俩线性相关
如这俩线性相关
线性变换
最基础的变换只有两种:旋转和拉伸
其他变换是复合变换
拉伸
矩阵D左乘一个S(对角矩阵)是拉伸或者压缩变化,对于原来的方向是没有变化的
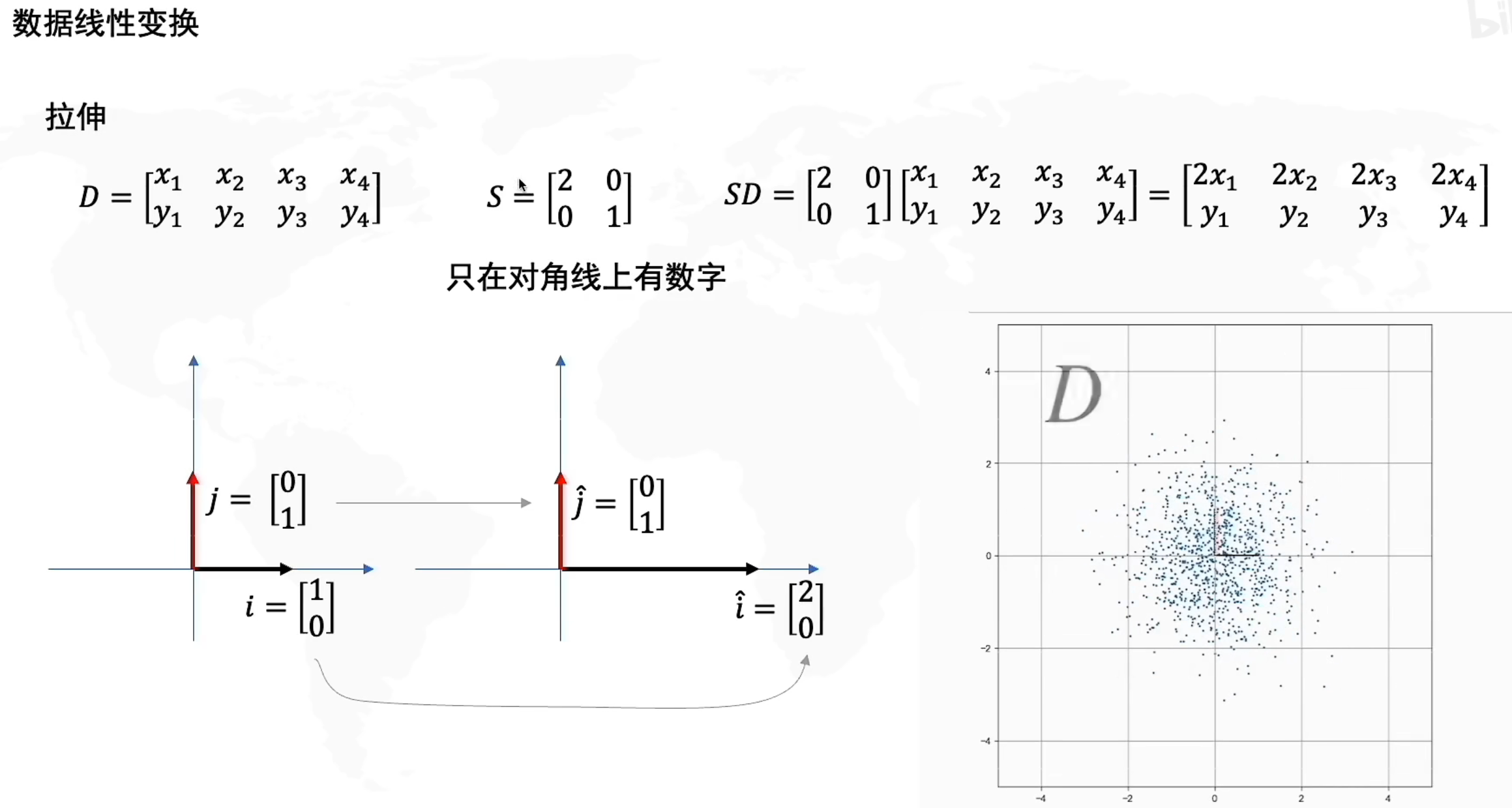
如上 :y不变,x变为原来2倍
旋转
矩阵D左乘一个R(酉矩阵)是旋转操作
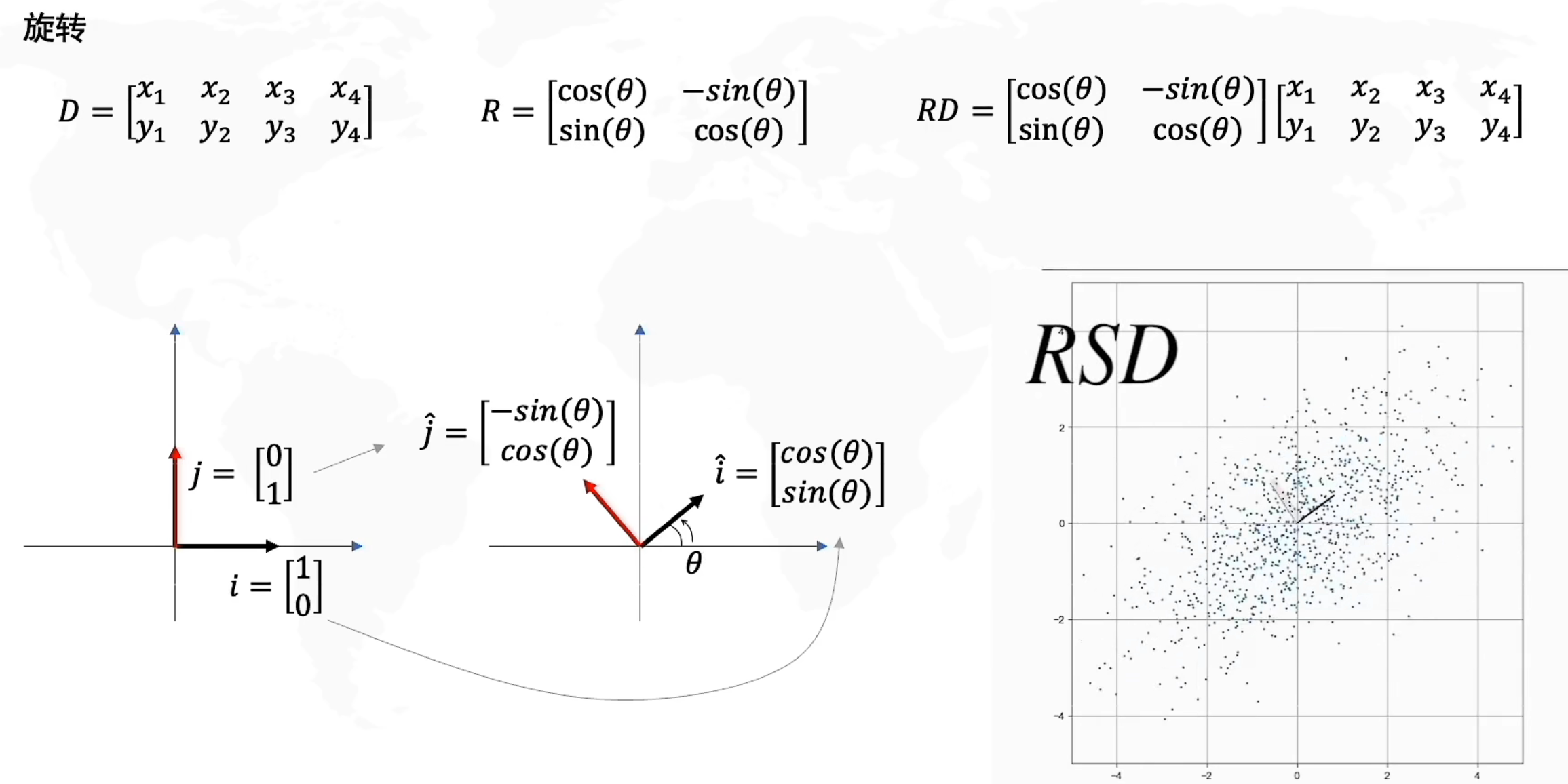
经过线性变化后必须遵守的原则:
- 直线依旧是直线
- 原点保持固定
把线性代数看做“保持网格线平行且等距分布”的变换

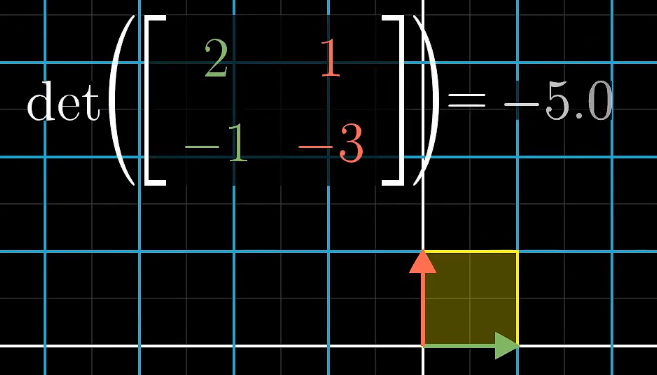
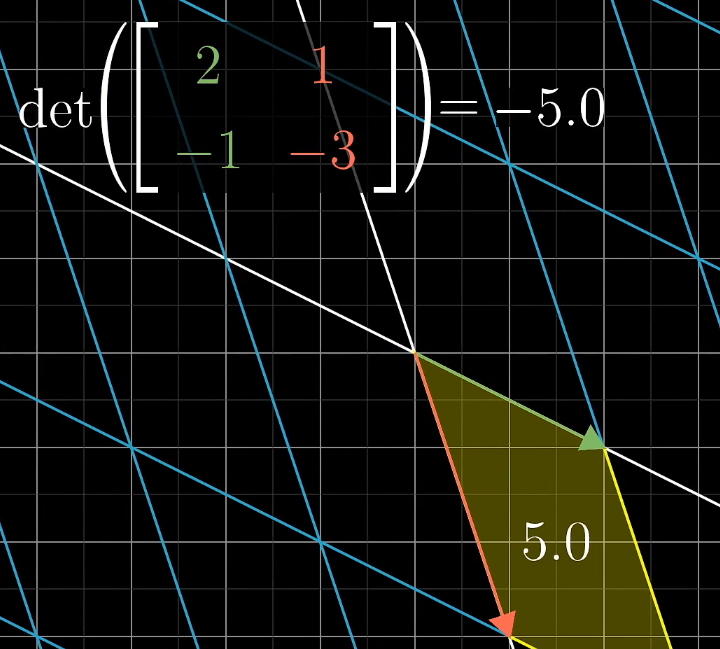
行列式
determinat
- 将行列式理解为:经过线性变换改变区域面积的比例
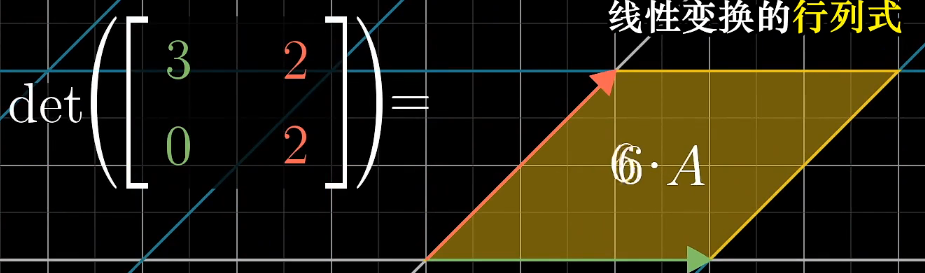
-
负值的理解:空间发生了翻转(i和j的相对位置发生了变化)
-
- 其绝对值仍为面积改变的比例
逆矩阵、线性空间
线性方程组
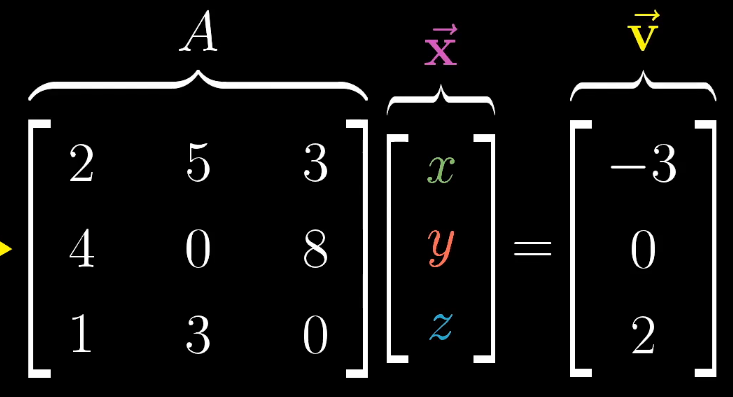
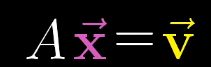
将线性方程组转化为矩阵
将矩阵A理解为空间中的一种线性变换(拉伸+旋转)
因此AX = V可以理解为通过线性变换可以将x变为v
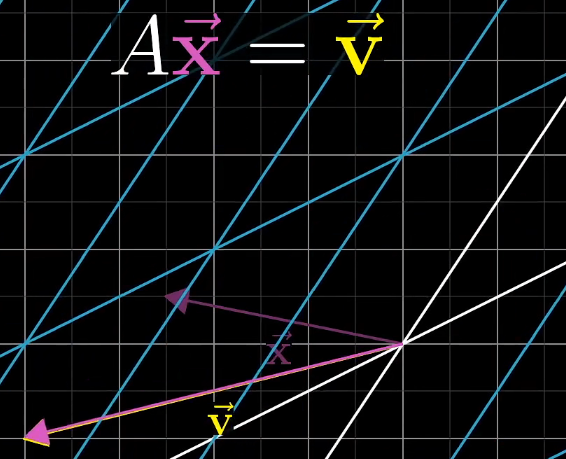
判断该线性方程组是否有唯一解
取决于行列式det
-
det ≠ 0 有唯一解
-
- A-1就存在,通过A-1可以还原该线性变换
- det ≠ 0 体现在空间中原本空间的维度不发生改变,只是发生一定比例的面积变化
- 上面的AX = V变换后空间仍然是二维空间,但是如果变换后i和j重叠,则不存在唯一解,不存在一个线性变换可以将一个线转换为一个面
-
det = 0没有唯一解
-
- 解可能存在
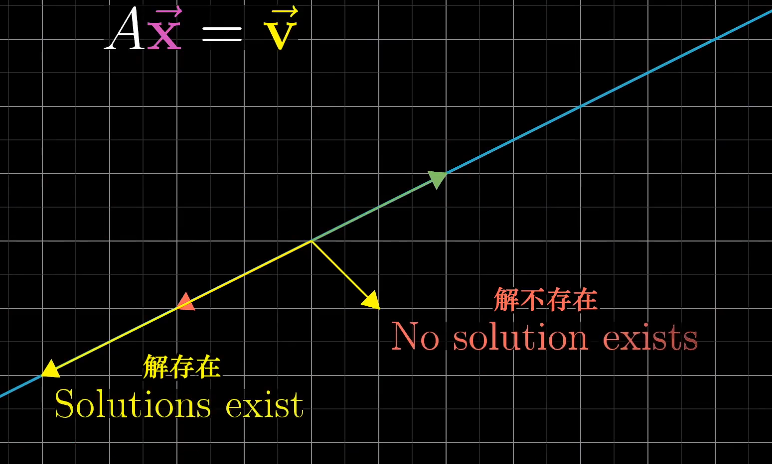
- 存在降维(秩)即rank < column
逆矩阵
那么逆矩阵就很好理解了,就是进行上面这个变换的一个逆变换
- 旋转


- 剪切


因此A-1A即不发生变化的矩阵

秩Rank
把秩理解为列空间的维度,列就是基向量
- 对于2*2的矩阵,r最大为2(det≠0时)r为2表示基向量可以张成一个二维空间
- r = 列数时,称为Full Rank 即满秩
- 零向量一定在列空间中(线性变换一定满足原点不变)
- 对于满秩矩阵,只有原点不变

矩阵求解
没啥用,理解矩阵更重要
https://www.bilibili.com/video/BV1zu41197pL/?spm_id_from=pageDriver&vd_source=5500fef761fd3ab451b9bbe518cd5cc6
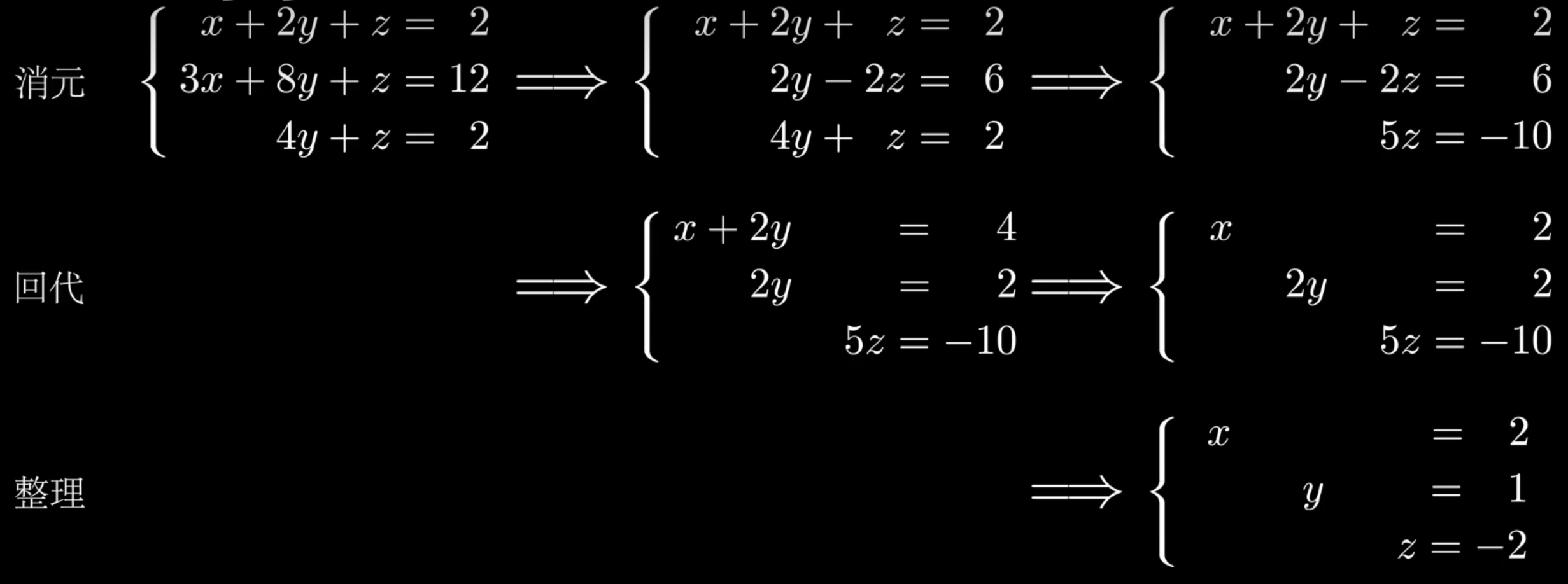

- 消元(高斯消元法) 行阶梯矩阵
- 回代
- 整理
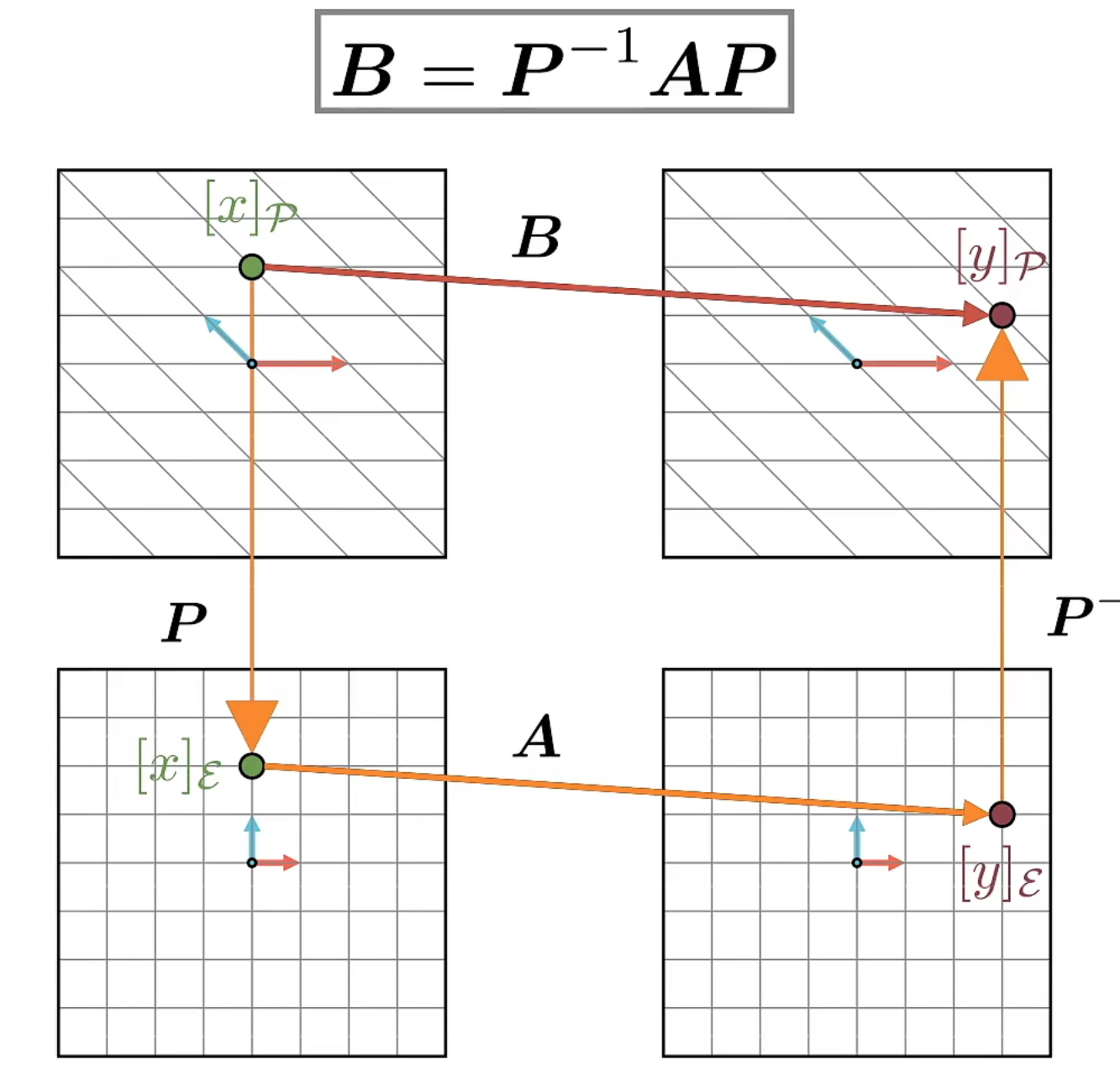
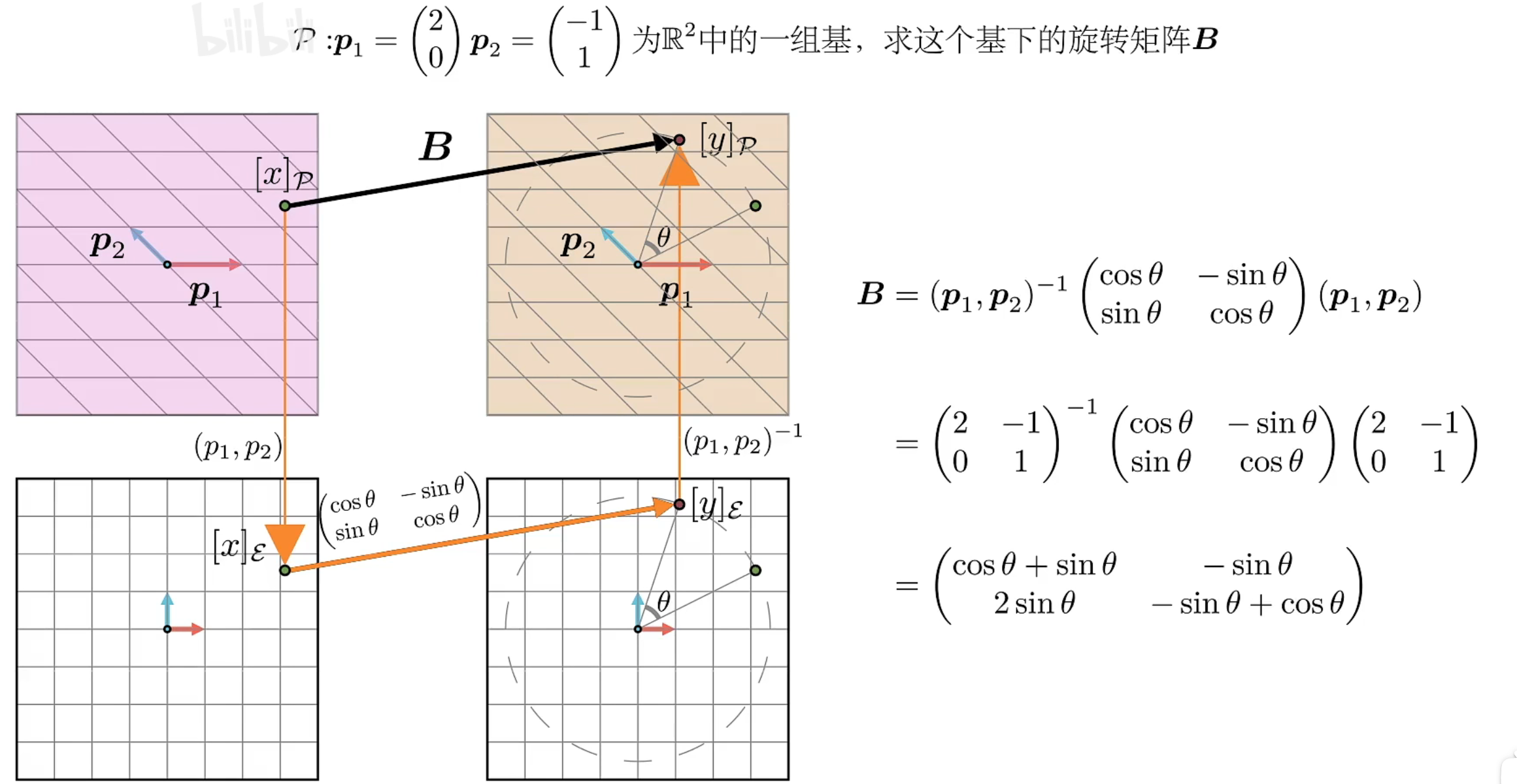
相似矩阵
B是在非正交基上的线性变换(矩阵)
通过以下操作可以转化为在正交基上的相似矩阵A
https://www.bilibili.com/video/BV1zu411673J/?spm_id_from=pageDriver&vd_source=5500fef761fd3ab451b9bbe518cd5cc6
点积 叉积
矩阵相乘
矩阵相乘表示的是线性变换的先后顺序
如下表示先进行B变换,再进行A变换,实际上可以融合为一个C变化(也是2*2)
A=[[2 1]
[1 1]]
B=[[3 1]
[1 1]]
AB
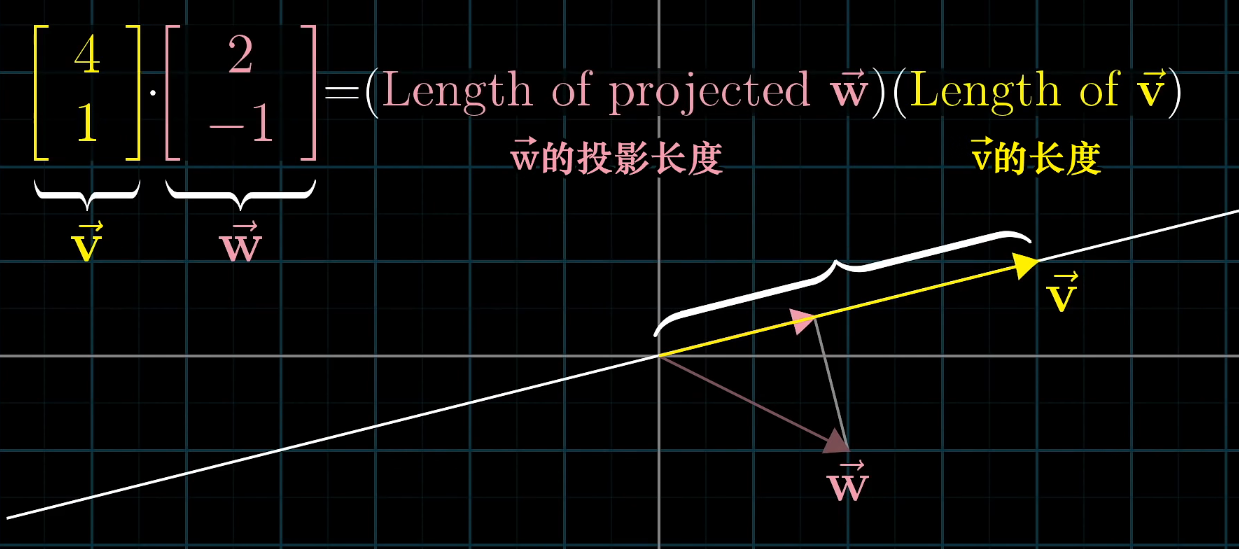
向量点积 Dot product
数学表示v·w = |v的投影长度||w|
- dot > 0 表示同向
- < 0 表示反向
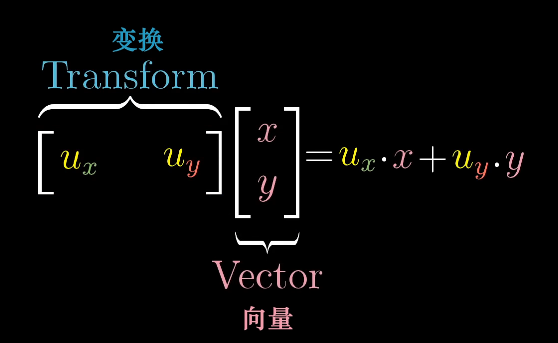
从线性变换看向量点积
- u·x u是变换矩阵 x是向量
- 基向量i、j经过变换矩阵后从二维变为一维直线
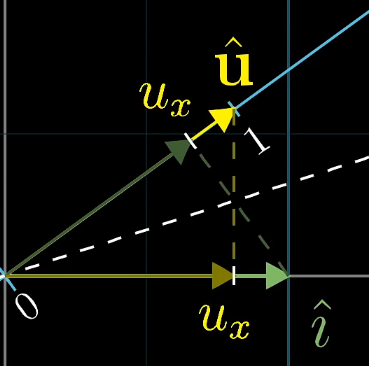
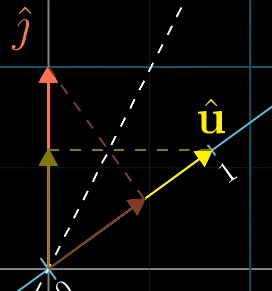
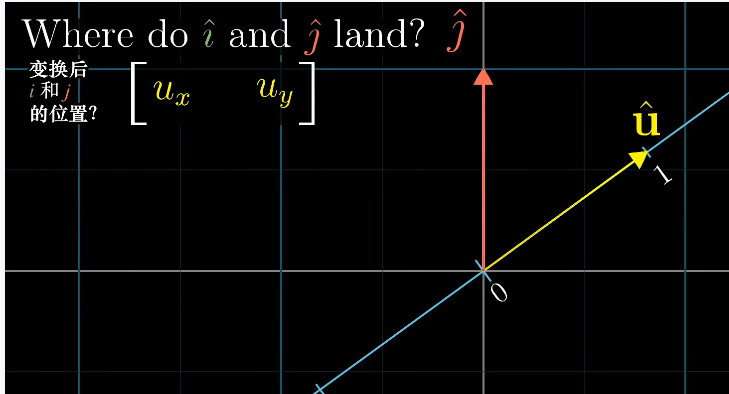
- 现在向量x就变为了直线上的一个点
- 之前一直不理解为什么向量点积之后变为一个具体的值,现在从维度上理解就很好理解了,一维直线由无数的点组成向量点积就是二维到一维转换的一个过程
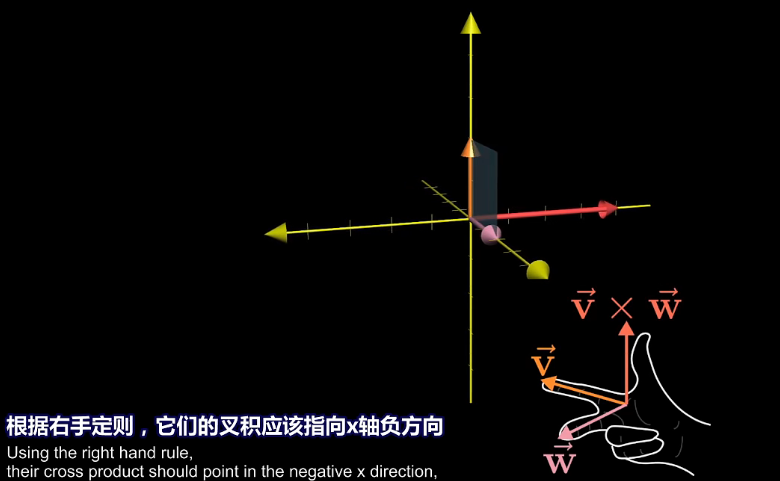
向量叉积
- v × w = p 叉乘结果是向量
- 向量长度 = 两向量围成的平行四边形的面积
- 方向用右手定则

计算叉乘的方法
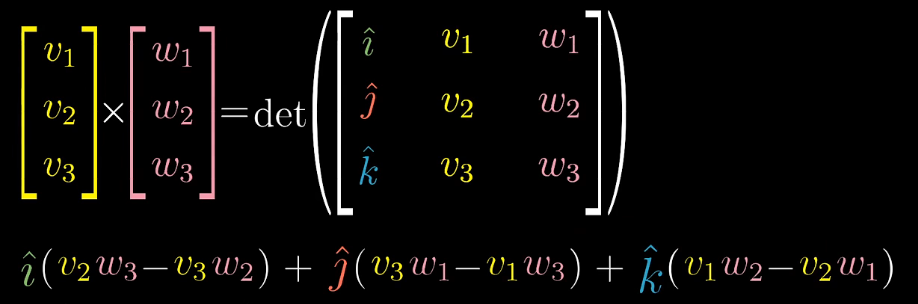
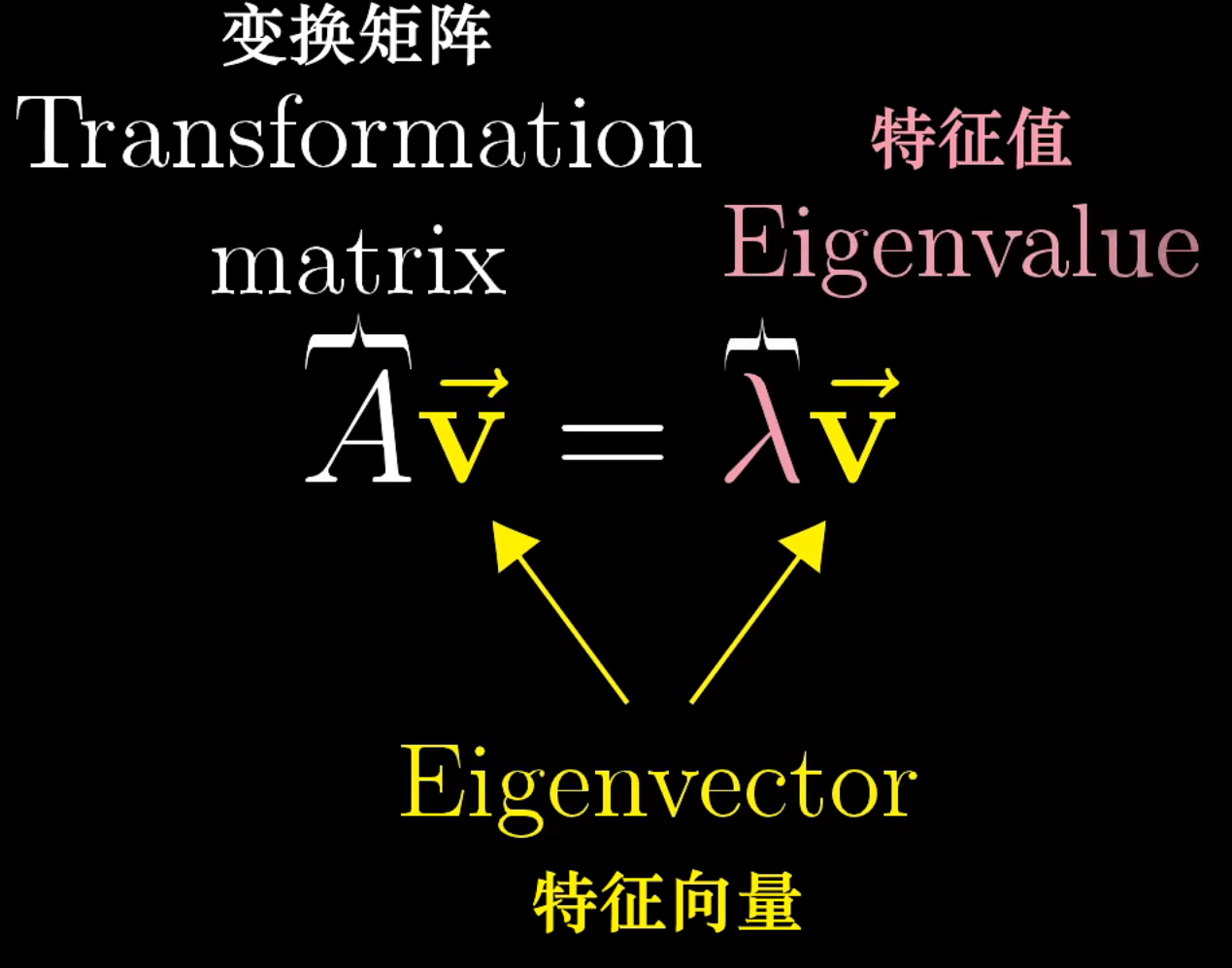
特征值 特征向量
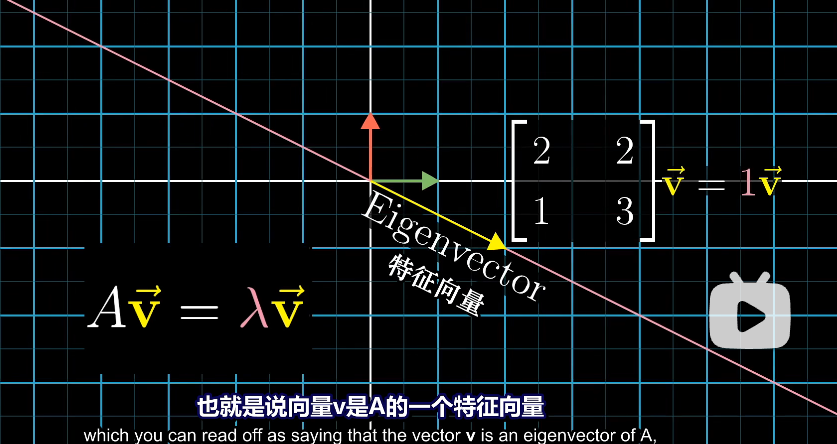
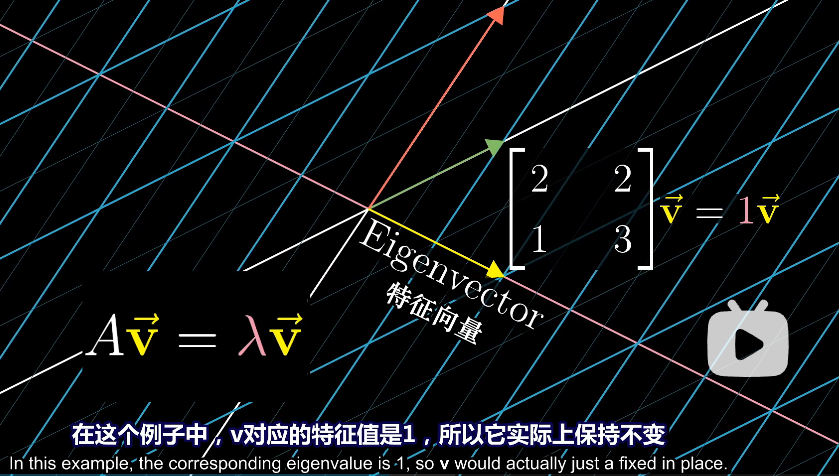
特征向量表现公式如下
- 对于这个向量进行A矩阵线性变换,等效于对其进行[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-HunDMy4t-1659017659081)(https://myblogimgbed.oss-cn-shenzhen.aliyuncs.com/img/e520c061a407db472027709bf3f73290.svg)]倍的缩放操作
- 即这个向量不发生旋转操作
- 二维线性变换不一定存在特征值
如:效果为旋转90°的矩阵,除了零向量以外,所有向量都发生空间位置改变
- 一个特征值可能对应多个特征向量
如:对于 这种变换,平面中每一个向量都是特征向量
这种变换,平面中每一个向量都是特征向量
- 对角矩阵
 所有基向量(列向量)都是特征向量,矩阵的对角元是特征值
所有基向量(列向量)都是特征向量,矩阵的对角元是特征值
特征基
引入特征基可以方便某些运算,如计算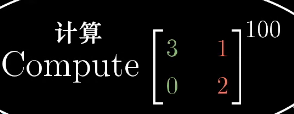 这种非对角矩阵
这种非对角矩阵
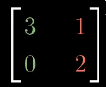 可以视为对原空间中某向量进行一种同时具有旋转加缩放的线性变换
可以视为对原空间中某向量进行一种同时具有旋转加缩放的线性变换- 我们通过
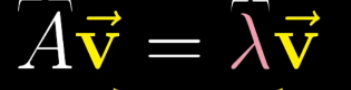
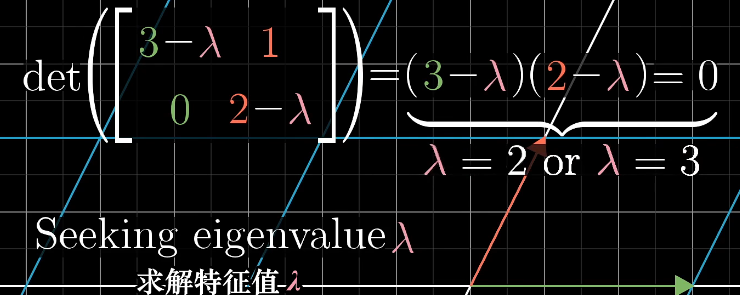 求特征值
求特征值 - 代入特征值求特征向量
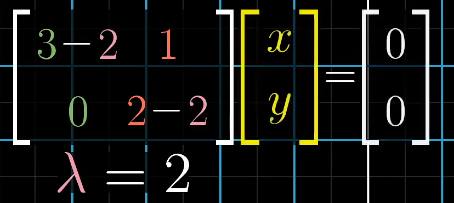
- 得到特征基矩阵

- 那么现在我们可以先左乘特征基矩阵,进行基转换
- 那么现在在这个新的基的基础上
 就是一种只有缩放的线性变换,即对角矩阵,那么可以进行100次方该操作
就是一种只有缩放的线性变换,即对角矩阵,那么可以进行100次方该操作 - 最后再用特征基逆矩阵转化回来
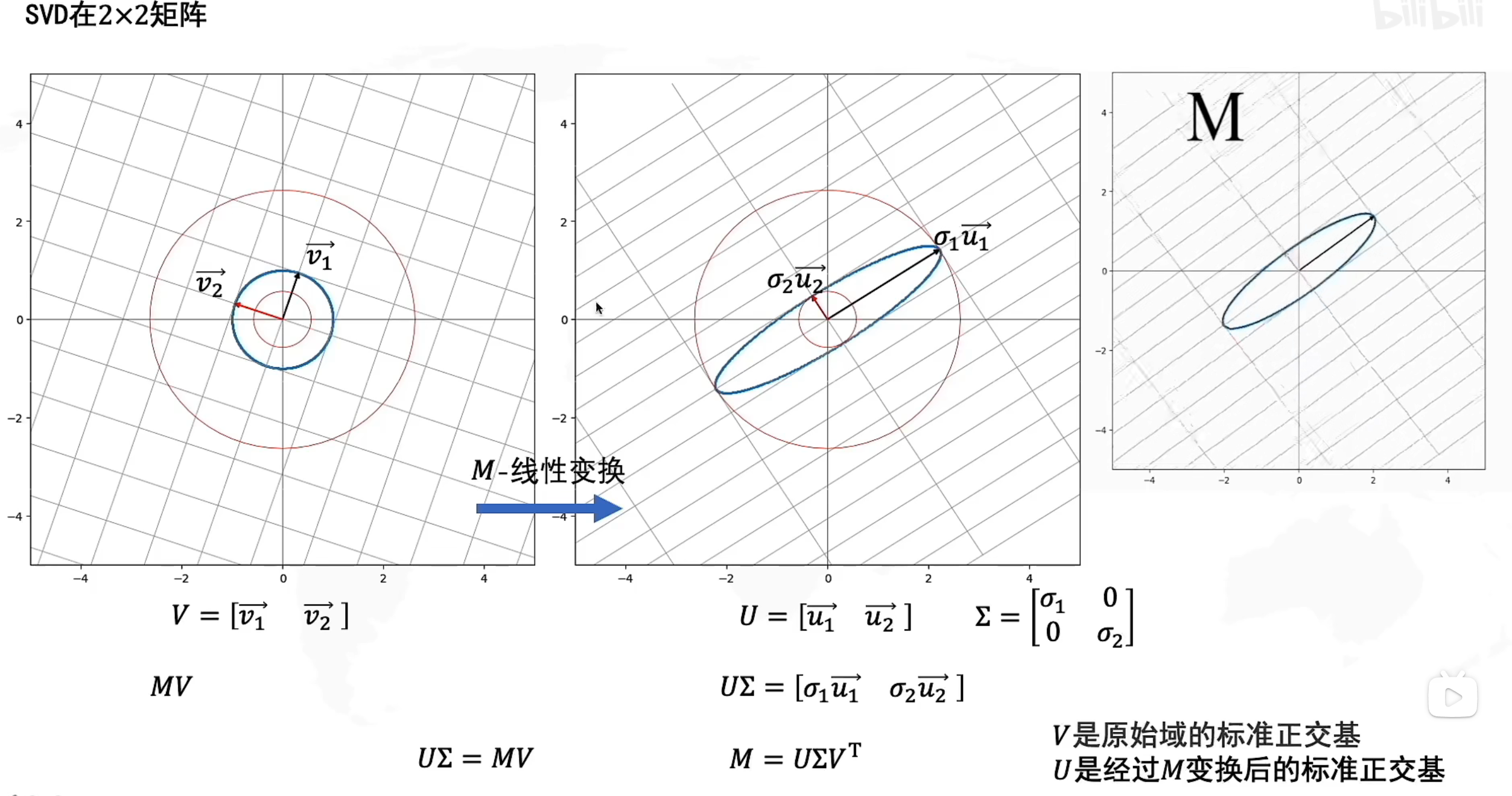
奇异值分解SVD
https://www.bilibili.com/video/BV16A411T7zX?spm_id_from=333.337.search-card.all.click&vd_source=5500fef761fd3ab451b9bbe518cd5cc6
SVD
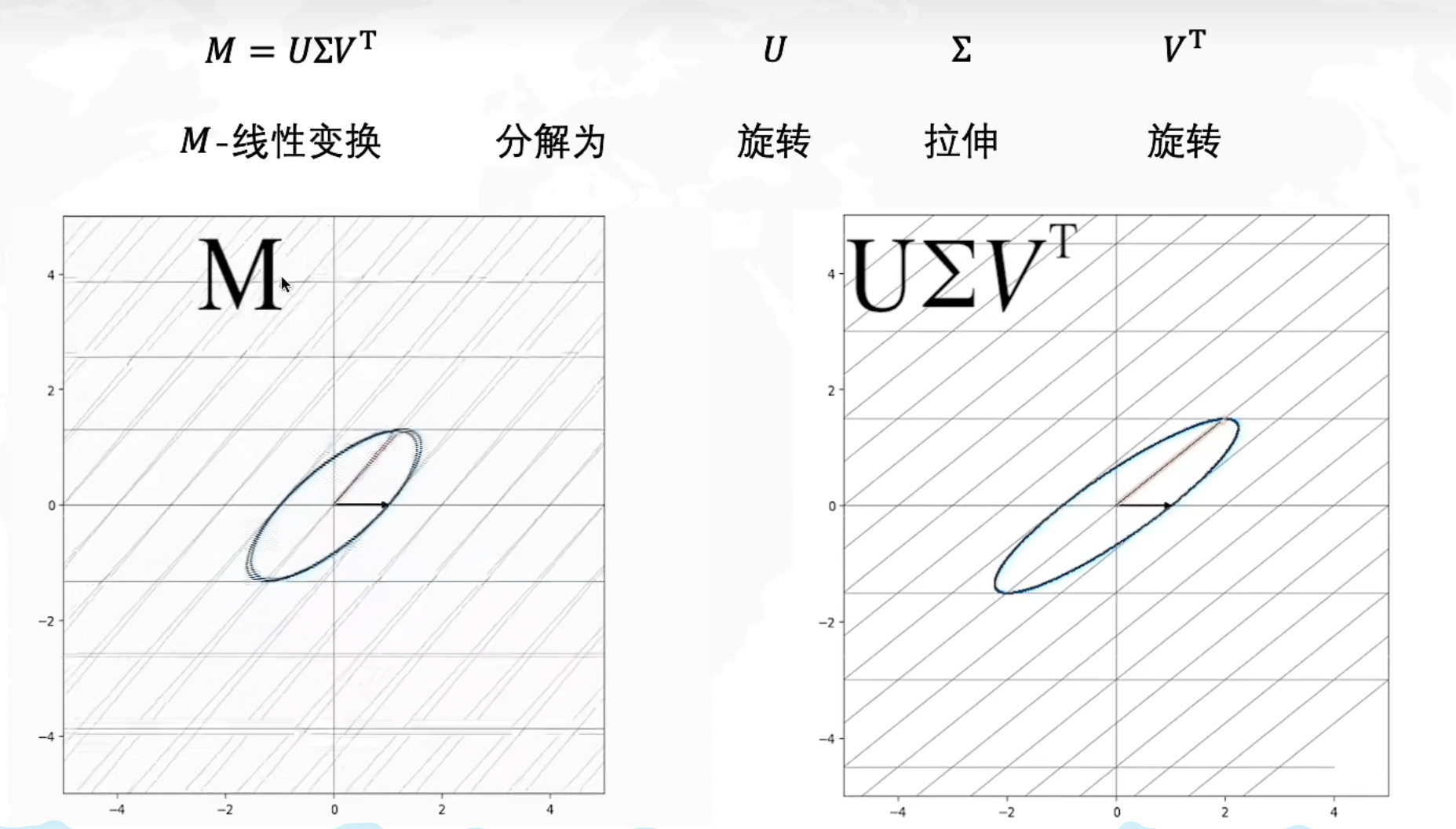
在原始域中的一个正交基V经过M矩阵的线性变换后,变为了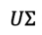 U是正交基
U是正交基 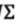 是拉伸变换
是拉伸变换
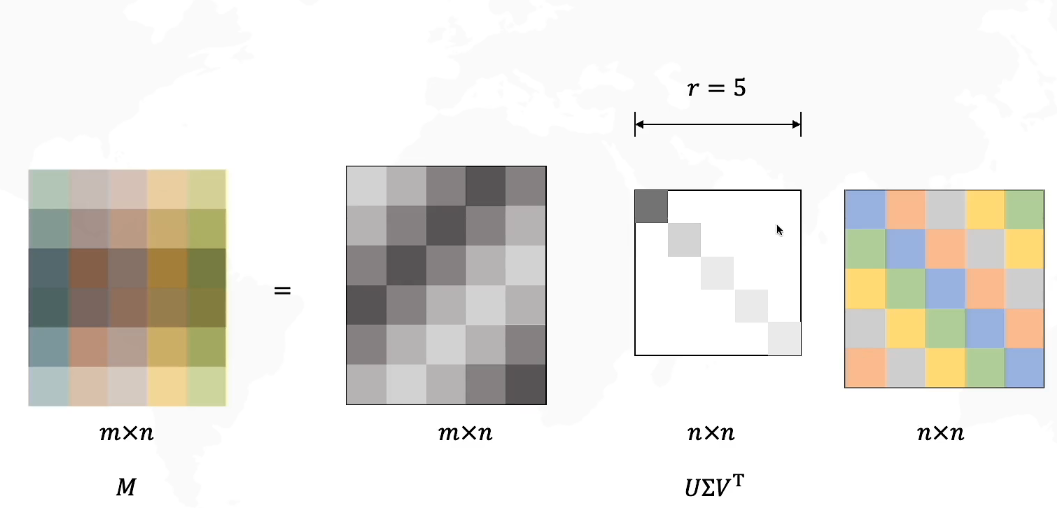
可以用于图像压缩,特征抽取
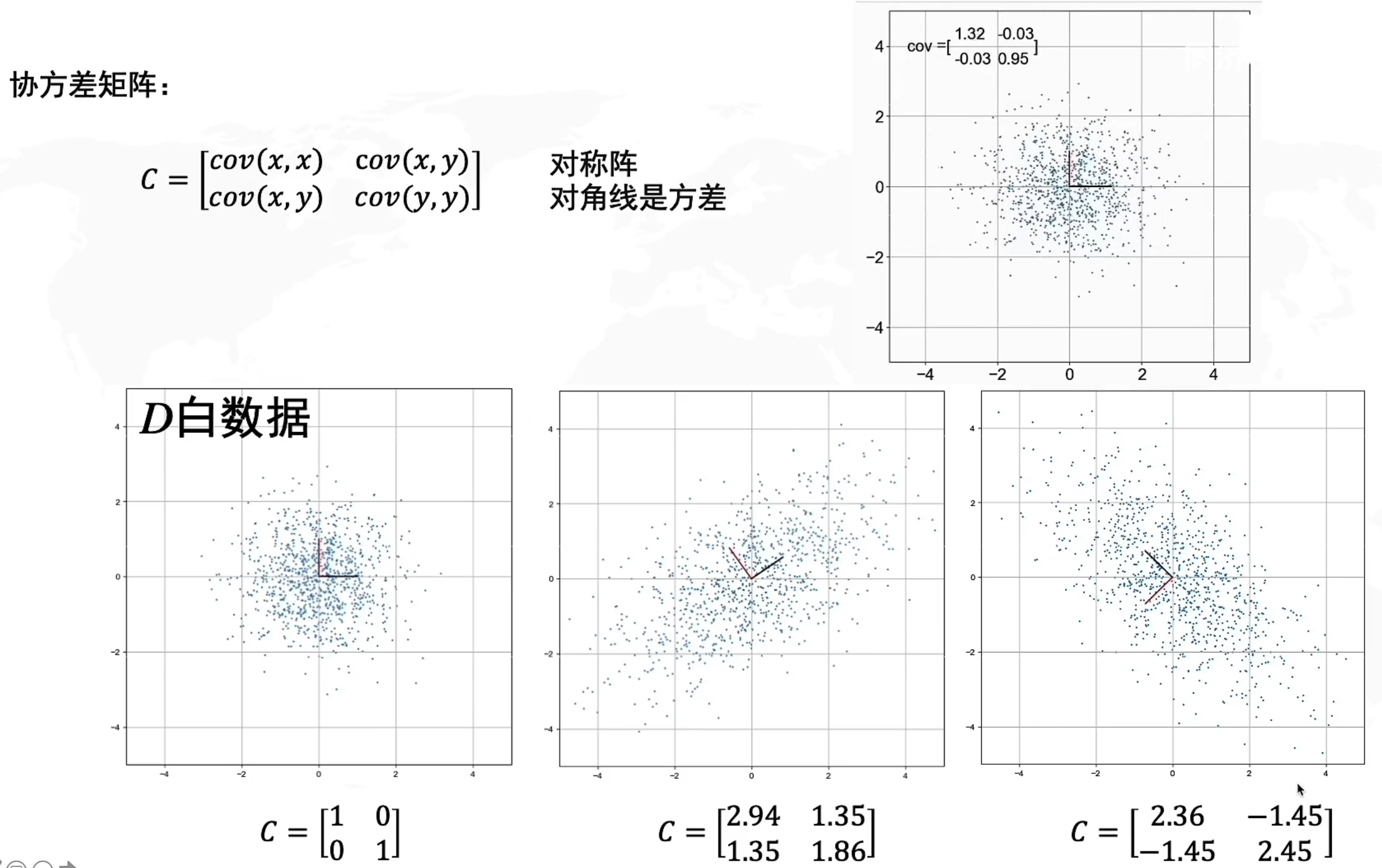
协方差

反映的是数据的相关性
- > 0 正相关
- < 0 负相关
- = 0 无关
协方差矩阵