Robust Principal Component Analysis?（PCP）

Candes E J, Li X, Ma Y, et al. Robust principal component analysis[J]. Journal of the ACM, 2011, 58(3).

引

这篇文章，讨论的是这样的一个问题：
$M = L_0 + S_0$

有这样的一个矩阵 $M \in \mathbb{R}^{n_1 \times n_2}$，它由一个低秩的矩阵 $L_0$和稀疏矩阵 $S_0$混合而成，那么，能否通过 $M$将 $L_0$和 $S_0$分别重构出来？而且，最关键的是，也是这篇文章的亮点所在：对于 $L_0$和 $S_0$仅有一丢丢的微弱的假设。

一些微弱的假设：

关于 $L_0$:
低秩矩阵 $L_0$不稀疏，这个假设很弱，但有意义。因为如果 $M=e_1e_1^*$(文章采用 $*$作为转置符号，这里沿用这种写法)，即只有左上角第一个元素非零，那么这个矩阵如何分解为低秩和稀疏呢，因为压根没法区分。作者引入incoherence condition(不连贯条件？抱歉，不晓得如何翻译)：
假设 $L_0$的SVD分解为：
$L_0 = U\Sigma V^*=\sum \limits_{i=1}^r \sigma_i u_i v_i^*$
其中 $r = \mathrm{rank}(L_0)$, $\sigma_i$为奇异值，并且， $U = [u_1, \ldots, u_r]$, $V = [v_1, \ldots, v_r]$。
incoherence condition:

分析这些条件可以发现， $U,V$的每一行的模都不能太大， $UV^*$的每个元素同样不能太大，所以最后结果 $L_0$的各个元素的大小会比较均匀，从而保证不稀疏？

关于 $S_0$:

类似地，需要假设 $S_0$不低秩，论文另辟蹊径，假设 $S_0$的基为 $m=\mathrm{Card}(S_0)$，其支撑(support)定义为：
$\Omega = \{(i,j)| [S_0]_{i,j} \ne 0\}$
论文假设 $S_0$的支撑 $\Omega$从一个均匀分布采样。即， $S_0$不为零的项为 $m$，从 $n_1\times n_2$个元素中挑选 $m$个非零的组合有 $\mathrm{C}_{n_1 \times n_2}^m$，论文假设每一种组合被采样的概率都是相同的。事实上，关于 $S_0$元素的符号，论文在后面说明，符号固定或者随机（服从伯努利分布），都能将 $L_0,S_0$恢复出来。

问题的解决

论文反复强调，多么令人惊讶，多么不可思议，事实上的确如此，上述问题只需求解一个形式非常简单的凸优化问题：

其中 $\|L\|_* = \sum \limits_{i=1}^r \sigma_i(L)$为其核范数。

论文给出了以下结论：


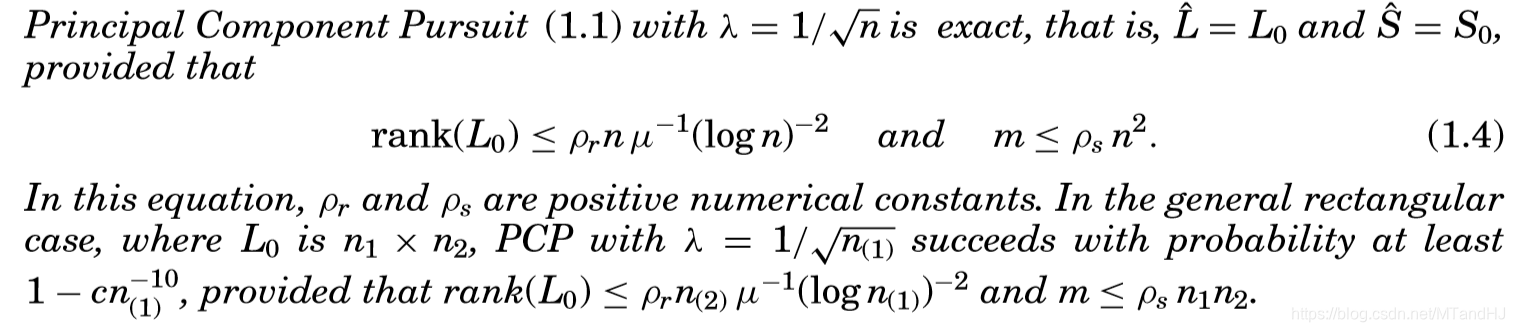
即：令 $n_{(1)}= \max(n_1, n_2), n_{(2)} = \min (n_1, n_2)$，对于任意矩阵 $M = L_0 + S_0 \in \mathbb{R}^{n_1 \times n_2}$，只要 $L_0$和 $S_0$满足上面提到的假设，那么就存在常数 $c$使得，PCP的解（即（1.1）的解，且 $\lambda= 1/ \sqrt{n_{(1)}}$） $\hat{L}$和 $\hat{S}$有 $1-c n_{(1)}^{-10}$的概率重构 $L_0$， $S_0$，即 $\hat{L}=L_0$， $\hat{S}=S_0$。并且有下列性质被满足 $\mathrm{rank}(L_0) \le \rho_r n_{(2)} \mu^{-1} (\log n_{(1)})^{-2},m \le \rho_s n_1 n_2$。

这个结果需要说明的几点是，常数 $c$是根据 $S_0$的支撑 $\Omega$决定的（根据后面的理论，实际上是跟 $\|\mathcal{P}_{\Omega} \mathcal{P}_{T}\|$有关），另外一点是， $\lambda = 1 / \sqrt{n_{(1)}}$。是的，论文给出了 $\lambda$的选择（虽然这个选择不是唯一的），而且，这个值是通过理论分析得到的。

关于问题 (1.1)的求解有很多现成的算法，这篇论文大量篇幅用于证明上述的理论结果，只在最后提到利用ALM（Augmented Largrange multiplier）方法有很多优势，算法如下：

其中 $\mathcal{S}_{\tau}[x] = \mathrm{sgn} (x) \max (|x| - \tau, 0)$, $\mathcal{D}_{\tau} (X)=U\mathcal{S}_{\tau}(\Sigma)V^*,X=U\Sigma V^*$。

ALM算法实际上是交替最小化下式：

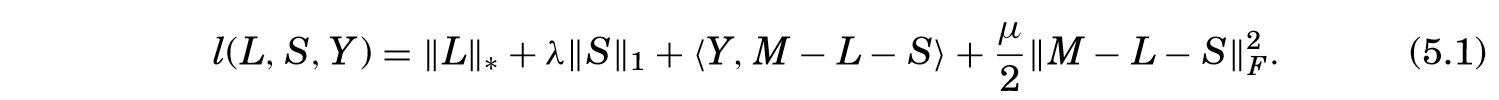
其中 $<A, B>:= \mathrm{Tr(A^TB)}$。

固定 $L, Y$,实际上就是最小化：
$\min \quad \lambda \|S\|_1 + <Y, -S> + \frac{\mu}{2}\mathrm{Tr}(S^TS -2S^T(M-L))$
其在 $S$处的导数(虽然有些点并不可导)为：
$\lambda \mathrm{sgn}(S) - Y + \mu S-\mu(M-L)$
实际上，对于每个 $S_{i,j}$，与其相关的为：
$a S_{i, j}^2 + b S_{i,j}+c|S_{i,j}|, \alpha > 0$
关于最小化这个式子，我们可以得到：
$S_{i,j}= \left \{ \begin{array}{ll} -\frac{b+c}{2a} & -\frac{b+c}{2a} \ge 0 \\ -\frac{b-c}{2a} & -\frac{b-c}{2a} \le 0 \\ 0 & else \end{array} \right.$
实际上就是 $S_{i,j}= \mathcal{S}_{c/2a}(-b/2a)$，对 $S$拆解，容易得到固定 $L,Y$的条件下， $S$的最优解为：
$\mathcal{S}_{\lambda / \mu}(M-L+\mu^{-1}Y)$
当 $S, Y$固定的时候：

实际上就是最小化下式：
$\|L\|_* + <Y, -L> + \frac{\mu}{2} \mathrm{Tr(L^TL-L^T(M-S))}$
观测其次梯度：
$UV^*+W-Y+\mu L - \mu(M-S)$
其中 $L=U\Sigma V^*，U^*W=0,WV=0,\|W\| \le 1$， $\|X\|$为 $X$的算子范数。
最小值点应当满足 $0$为其次梯度，即：
$L = -\mu^{-1}UV^*-\mu^{-1}W+\mu^{-1}Y + M-S$
有解。
令 $A = M-S+\mu^{-1}Y$
则：
$L = -\mu^{-1}UV^*-\mu^{-1}W+A \\ \Rightarrow \Sigma=-\mu^{-1}I+U^*AV$
假设 $A=U_A\Sigma_A V_A^*$，那么：
$\Sigma=-\mu^{-1}I+U^*U_A\Sigma_A V_A^*V$
如果我们令 $U=U_A,V=V_A$，则：
$\Sigma = \Sigma_A-\mu^{-1}I$
但是我们知道， $\Sigma$的对角元素必须大于等于0，所以我可以这样构造解：
假设 $\Sigma_A$的对角元素，即奇异值降序排列 $\sigma_1(A) \ge \sigma_2(A) \ldots \sigma_k(A) \ge \mu^{-1} > \sigma_{k+1}(A) \ge \ldots \ge \sigma_r(A)$，相对于的向量为 $u_1(A),\ldots,u_r(A)$和 $v_1{A},\ldots, v_r(A)$。我们令
$L=\sum \limits_{i=1}^k (\sigma_i(A)-\mu^{-1})u_i(A)v_i^T(A) \\ W = \sum \limits_{i=k+1}^{r} \mu \sigma_i(A)u_i(A)v_i^T(A)$
容易验证 $U^*W=0,WV=0$，又 $\mu^{-1} > \sigma_i(A), i > k$，所以 $\mu \sigma_i(A) < 1$，所以 $\|W\| \le 1$也满足。同样的，次梯度为0的等式也满足，所以 $L$就是我们要找到点（因为这个是凸函数，极值点就是最小值点）。

理论

这里只介绍一下论文的证明思路。
符号：

去随机

论文先证明，如果 $S_0$的符号是随机的（伯努利分布），在这种情况能恢复，那么 $S_0$的符号即便不随机也能恢复。

Dual Certificates(对偶保证？)

引理2.4

引理2.4告诉我们，只要我们能找到一对 $(W, F)$，满足 $UV^*+W=\lambda(sgn(S_0)+F)$。 $(L_0,S_0)$是优化问题(1.1)的唯一解。但是不够，因为这个条件太强了， $W, F$的构造是困难的。

引理2.5

进一步改进，有了引理2.5。

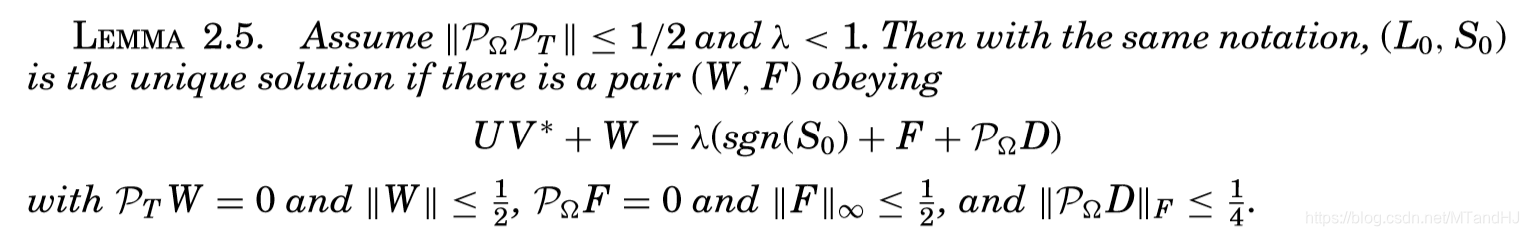
引理2.5的意义在哪呢？它意味着，我们只要找到一个 $W$，满足：

那么， $(L_0,S_0)$就是问题 $(1.1)$的最优解，而且是唯一的。

Golfing Scheme

接下来，作者介绍一种机制来构造 $W$，并且证明这种证明能够大概率保证 $W$能够满足上述的对偶条件。作者将 $W = W^L + W^S$分解成俩部分，俩部分用不同的方式构造：

接下的引理和推论，总结起来便是最后的证明：




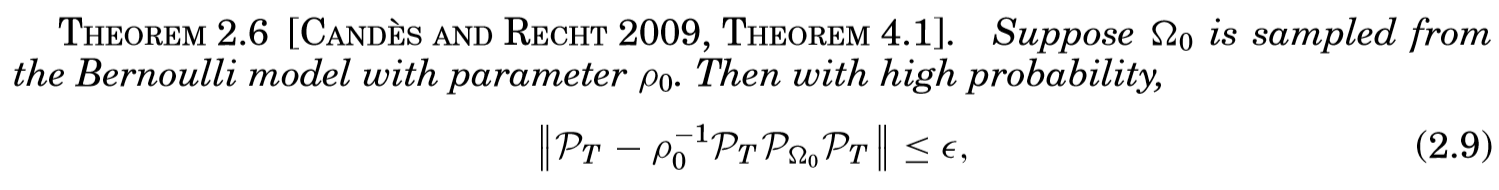
通过引理2.8和2.9，再利用范数的三角不等式，容易验证 $W = W^L+W^S$满足对偶条件。
最后提一下，定理的概率体现在哪里，在对偶条件的引理中，有这么一个假设 $\|\mathcal{P}_{\Omega}\mathcal{P}_T\| \le 1$和 $\|\mathcal{P}_{\Omega}\mathcal{P}_T\| \le 1/2$，这些条件并不一定成立，根据 $\Omega$的采样，成立的大概率的。

数值实验

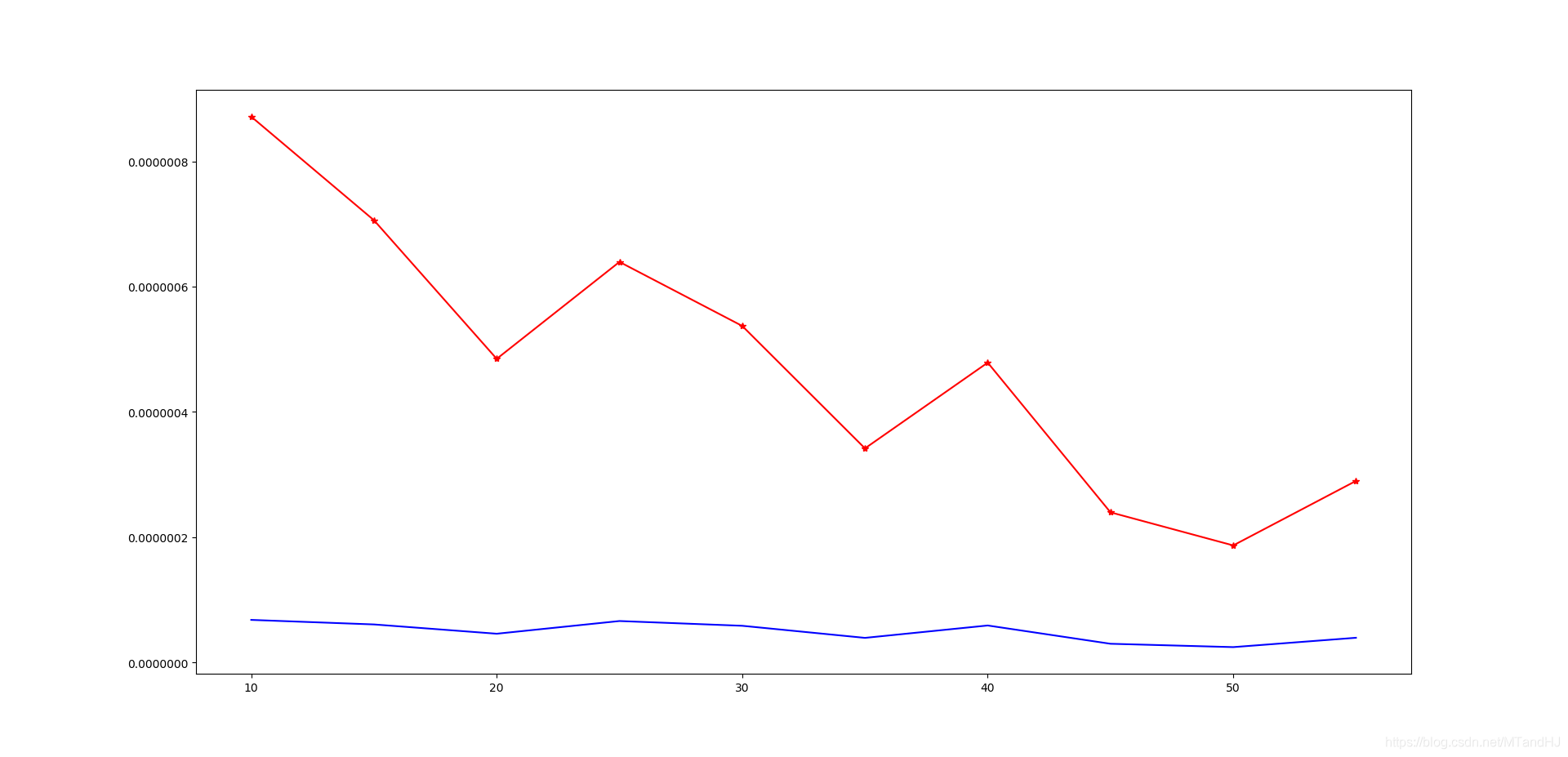
按照论文里，普通的人工生成矩阵，实验下来和论文的无异。也的确， $S_0$的规模大小（每个元素的大小）对能否恢复几乎没有影响，有影响的是 $S_0$的稀疏度。实验下来，稀疏度越高（0基越小），恢复的越好，而且差距蛮大的。

我们的实验， $L = XY$，其中 $X,Y \in \mathbb{R}^{500 \times 25}$依标准正态分布生成的， $S_0$是每个元素有 $\rho$的概率为 $100$， $\rho$的概率为 $-1$， $1-2\rho$的概率为0。 $\rho$我们选了 $1/10, 1/15, \ldots, 1/55$。
下面的图，红色表示 $\|\hat{L}-L_0\|_F/\|L_0\|_F$，蓝色表示 $\|\hat{S}-S_0\|_F/\|S_0\|_F$。因为每种情况我只做了一次实验，所以结果有起伏，但是趋势是在的。

比较有意思的是图片的拆解，我在马路上拍了31张照片，按照论文的解释，通过将照片拉成向量，再混合成一个矩阵 $M$，然后通过优化问题解出 $\hat{L}$和 $\hat{S}$，那么 $\hat{L}$的行向量（我做实验的时候是将一个照片作为一个行向量，论文里的是列向量）重新展成图片应该是类似背景的东西，而 $\hat{S}$中对应的行向量应该是原先图片中会动的东西。

照片我进行了压缩( $416 \times 233$)和灰度处理，处理 $M$用了1412次迭代，时间大概15分钟？比我预想的快多了。
我挑选其中比较混乱的图（就是车比较多的）：
第一组：
M:

L:

S:

第二组：

M:

L:

S:

第三组：

M:

L:

S:

比较遗憾的是， $\hat{S}$中都出现了面包车，我以为面包车会没有的，结果还是出现了。

代码

"""
Robust Principal Component Analysis?
"""


import numpy as np

class RobustPCA:

    def __init__(self, M, delta=1e-7):
        self.__M = np.array(M, dtype=float)
        self.__n1, self.__n2 = M.shape
        self.S = np.zeros((self.__n1, self.__n2), dtype=float)
        self.Y = np.zeros((self.__n1, self.__n2), dtype=float)
        self.L = np.zeros((self.__n1, self.__n2), dtype=float)
        self.mu = self.__n1 * self.__n2 / (4 * self.norm_l1)
        self.lam = 1 / np.sqrt(max(self.__n1, self.__n2))
        self.delta = delta

    @property
    def norm_l1(self):
        """返回M的l1范数"""
        return np.sum(np.abs(self.__M))

    @property
    def stoprule(self):
        """停止准则"""
        A = (self.__M - self.L - self.S) ** 2
        sum_A = np.sqrt(np.sum(A))
        bound = np.sqrt(np.sum(self.__M ** 2))
        if sum_A <= self.delta * bound:
            return True
        else:
            return False
    def squeeze(self, A, c):
        """压缩"""
        if c <= 0:
            return A
        B1 = np.where(np.abs(A) < c)
        B2 = np.where(A >= c)
        B3 = np.where(A <= -c)
        A[B1] = [0.] * len(B1[0])
        A[B2] = A[B2] - c
        A[B3] = A[B3] + c
        return A

	def newsvd(self, A):
        def sqrt(l):
            newl = []
            for i in range(len(l)):
                if l[i] > 0:
                    newl.append(np.sqrt(l[i]))
                else:
                    break
            return np.array(newl)
        m, n = A.shape
        if m < n:
            C = A @ A.T
            l, u = np.linalg.eig(C)
            s = sqrt(l)
            length = len(s)
            u = u[:, :length]
            D_inverse = np.diag(1 / s)
            vh = D_inverse @ u.T @ A
            return u, s, vh
        else:
            C = A.T @ A
            l, v = np.linalg.eig(C)
            s = sqrt(l)
            length = len(s)
            v = v[:, :length]
            D_inverse = np.diag(1 / s)
            u = A @ v @ D_inverse
            return u, s, v.T

    def update_L(self):
        """更新L"""
        A = self.__M - self.S + self.Y / self.mu
        u, s, vh = np.linalg.svd(A) #or self.newsvd(A)
        s = self.squeeze(s, 1 / self.mu)
        s = s[np.where(s > 0)]
        length = len(s)
        if length is 0:
            self.L = np.zeros((self.__n1, self.__n2), dtype=float)
        elif length is 1:
            self.L = np.outer(u[:, 0] * s[0], vh[0])
        else:
            self.L = u[:, :length] * s @ vh[:length]

    def update_S(self):
        """更新S"""
        A = self.__M - self.L + self.Y / self.mu
        self.S = self.squeeze(A, self.lam / self.mu)

    def update_Y(self):
        """更新Y"""
        A = self.__M - self.L - self.S
        self.Y = self.Y + self.mu * A

    def process(self):
        count = 0
        while not (self.stoprule):
            count += 1
            assert count < 10000, "something wrong..."
            self.update_L()
            self.update_S()
            self.update_Y()
        print(count)

注意到，我自己写了一个newsvd的方法，这是因为，在处理图片的时候，用numpy的np.linalg.svd会报memoryerror，所以就自己简单调整了一下。