title
有 种物品和一个容量是 的背包。
第 种物品最多有 件,每件体积是 ,价值是 。
求解将哪些物品装入背包,可使物品体积总和不超过背包容量,且价值总和最大。
输出最大价值。
输入格式
第一行两个整数, ,用空格隔开,分别表示物品种数和背包容积。
接下来有 行,每行三个整数 ,用空格隔开,分别表示第 i 种物品的体积、价值和数量。
输出格式
输出一个整数,表示最大价值。
数据范围
提示
本题考查多重背包的单调队列优化方法。
输入样例

4 5
1 2 3
2 4 1
3 4 3
4 5 2
输出样例:
10
analysis
在之前的二进制解法中,
数组省略了“阶段”这一维。当外层循环进行到
时,
表示从前
种物品中选出若干个放入背包,体积之和为
时,价值之和最大是多少。 倒序循环
,在状态转移时,考虑选取第
个物品的个数
:
- 画出能够转移到状态
的决策候选集合
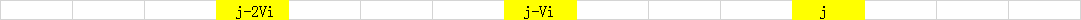
- 当循环变量
减小
时:
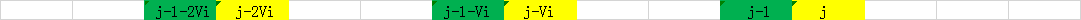
- 可以发现,相邻两个状态 和 对应的决策候选集合没有重叠,很难快速地从 对应的集合得到 对应的集合。
但是,我们适合考虑一下状态
和
:
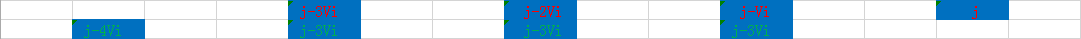
这两者对应的决策候选集合之间的关系,与我们前面讲解的单调队列题目非常相似,只有一个新决策加入候选集合、一个已有决策被排除。所以,我们应该把状态
按照除以
的余数分组,对每一组分别进行计算,不同组间的状态在阶段
不会互相转移:
余数为
——
余数为
——
余数为
——
把“倒序循环
”的过程,改为对每个余数
,倒序循环
,对应的状态就是
。第
种物品只有
个,故能转移到
的决策候选集合就是
。写出新的状态转移方程:
把外层循环
和
看做定值,当内层循环变量
减小
时,决策
的取值范围
的上下界均单调减小。状态转移方程等号右侧的石子仍然分为两部分,仅包含变量
的
和仅包含变量
的
。
综上所述,我们可以建立一个决策点
单调递减、数值
单调递减的队列,用于维护候选集合。对于每个
,执行单调队列的是三个惯例操作:
1.检查队头合法性,把大于
的决策点出队。
2.取队头为最优决策,更新
。
3.把新决策
插入队尾,入队前检查队尾单调性,排除无用决策。
整个算法的时间复杂度为
。
code
#include<bits/stdc++.h>
using namespace std;
const int maxn=1e3+10,maxv=2e4+10;
template<typename T>inline void read(T &x)
{
x=0;
T f=1, ch=getchar();
while (!isdigit(ch) && ch^'-') ch=getchar();
if (ch=='-') f=-1, ch=getchar();
while (isdigit(ch)) x=(x<<1)+(x<<3)+(ch^48), ch=getchar();
x*=f;
}
int f[maxv],V[maxn],W[maxn];
inline int calc(int i,int x,int k)
{
return f[x+k*V[i]]-k*W[i];
}
int C[maxn],q[maxv];
int main()
{
int n,m;read(n);read(m);
memset(f,0xcf,sizeof(f));
f[0]=0;
for (int i=1; i<=n; ++i)
{
read(V[i]),read(W[i]),read(C[i]);
for (int x=0; x<V[i]; ++x)
{
int l=1,r=0;
int maxp=(m-x)/V[i];
for (int k=maxp-1; k>=max(maxp-C[i],0); --k)
{
while (l<=r && calc(i,x,q[r])<=calc(i,x,k)) --r;
q[++r]=k;
}
for (int p=maxp; p>=0; --p)
{
while (l<=r && q[l]>p-1) ++l;
if (l<=r) f[x+p*V[i]]=max(f[x+p*V[i]],calc(i,x,q[l])+p*W[i]);
if (p-C[i]-1>=0)
{
while (l<=r && calc(i,x,q[r])<=calc(i,x,p-C[i]-1)) --r;
q[++r]=p-C[i]-1;
}
}
}
}
int ans=0;
for (int i=1; i<=m; ++i) ans=max(ans,f[i]);
printf("%d\n",ans);
return 0;
}