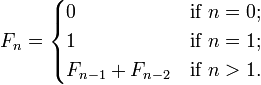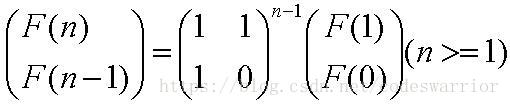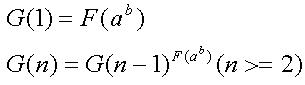Interesting Fibonacci HDU 2814(循环节)(欧拉降幂)

题干：

给定a,b,n,c;求G(n)%c的值。

思路：

前置的思想准备有：
巨大的斐波那契数列
矩阵快速幂

详细的证明可以看下这位大佬的详解
说一下解释和坑：
设F[i]为斐波那契数列的第i项。
G(n)= ${F[a^b]^{F[a^b]^{n-1}} }$%c

因为指数 ${F[a^b]}^{n-1}$会很大，所以在%c的时候先欧拉降幂。 ${F[a^b]}^{n-1}$% $φ(c)$+ $φ(c)$ (其中 $φ(c)$为c的欧拉函数)。

${F[a^b]}$可以用指数循环节来使 $a^b$减小，思路参考自巨大的斐波那契数列那个题。

其他的用快速幂解就行。

坑点：
输入数据范围在 $2^{64}$，所以需要unsigned long long和cin来输入。
快速幂求 $a^b$时，a可能很大，所以先对a%c。
当c=1时，整个F[]=0，所以G(n)=0;
当 $φ(c)$=1时， ${F[a^b]}^{n-1}$=1，所以G(n)= ${F[a^b]}$%c;

打表版：

#include <iostream>
#include <algorithm>
#include <cstdlib>
#include <cstdio>
#include <cstring>
#include <math.h>
using namespace std;
typedef unsigned long long ll;
int f[400][10000],F[10000];
ll qc(ll a,ll b,int c)
{
	a%=c;  //注意先模除
	ll ans=1;
	while(b)
	{
		if(b&1)
			ans=(ans*a)%c;
		a=(a*a)%c;
		b>>=1;
	}
	return ans%c;
}
ll ol(ll n)  //求欧拉函数
{
	ll ans=n;
	for(int i=2;i*i<=n;i++){
		if(n%i==0)
		{
			ans-=ans/i;
			while(n%i==0)
				n/=i;
		}
	}
	if(n>1)  ans-=ans/n;
	return ans;
}
int main()
{
	int t,c;
	for(int i=2;i<=300;i++){  //打表f[i][j]表示斐波的第j项模i的数
		f[i][0]=f[i][1]=1;
		for(int j=2;;j++){
			f[i][j]=(f[i][j-1]+f[i][j-2])%i;
			if(f[i][j]==1&&f[i][j-1]==1){
				F[i]=j-1;
				break;
			}
		}
	}
	cin>>t;
		for(int k=1;k<=t;k++)
		{
			ll a,b,n;
			cin>>a>>b>>n>>c;
			//cout<<a<<" "<<b<<" "<<endl;
			ll olc=ol(c);
			if(c==1)
			{
				cout<<"Case "<<k<<": 0"<<endl;
				continue;
			}
			if(olc==1)
			{
				ll fa=qc(a,b,F[c]);
				fa=f[c][fa-1];
				cout<<"Case "<<k<<": "<<fa%c<<endl;
				continue;
			}
			ll fa=qc(a,b,F[c]),fb=qc(a,b,F[olc]);
			//cout<<F[c]<<" "<<F[olc]<<endl;
			//cout<<fa<<" "<<fb<<endl;
			fa=f[c][fa-1];  //注意fa和fb减一
			fb=f[olc][fb-1];
			fb=qc(fb,n-1,olc);
			cout<<"Case "<<k<<": ";
			cout<<qc(fa,fb+olc,c)<<endl;
		}
	return 0;
}

非打表版：

#include <iostream>
#include <algorithm>
#include <cstdlib>
#include <cstdio>
#include <cstring>
#include <math.h>
using namespace std;
typedef unsigned long long ll;
int f[109000];
ll ol(ll n)
{
	ll ans=n;
	for(int i=2;i*i<=n;i++){
		if(n%i==0)
		{
			ans-=ans/i;
			while(n%i==0)
				n/=i;
		}
	}
	if(n>1)  ans-=ans/n;
	return ans;
}
int find(int c)
{
	memset(f,0,sizeof(f));
	f[0]=f[1]=1;
	for(int i=2;;i++){
		f[i]=(f[i-1]+f[i-2])%c;
		if(f[i]==1&&f[i-1]==1)
			return (i-1);
	}
}
ll qc(ll a,ll b,int c)
{
	a%=c;
	ll ans=1;
	while(b)
	{
		if(b&1)
			ans=(ans*a)%c;
		a=(a*a)%c;
		b>>=1;
	}
	return ans%c;
}
int main()
{
	fflush(stdin);
	ll a,b,n;
	int c,t;
	scanf("%d",&t);
		for(int k=1;k<=t;k++){
			cin>>a>>b>>n>>c;
			int olc=ol(c);
			if(c==1)
			{
				cout<<"Case "<<k<<": ";
				cout<<0<<endl; 
				continue;
			}
			if(olc==1)
			{
				int F=find(c);
				ll ans=qc(a,b,F);
				cout<<"Case "<<k<<": ";
				cout<<(f[ans-1]%c)<<endl; 
				continue;
			}
			int F=find(c);
			//cout<<F<<" "<<F1<<endl;
			ll ans=qc(a,b,F);
			int temp=f[ans-1];
			ll F1=find(olc);
			ll ans1=qc(a,b,F1);
			ans1=qc(f[ans1-1],n-1,olc);
			cout<<"Case "<<k<<": ";
			cout<<qc(temp,ans1+olc,c)<<endl; 
		}
	return 0;
}