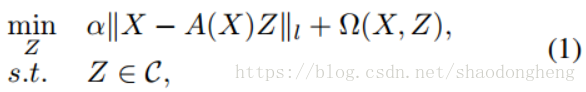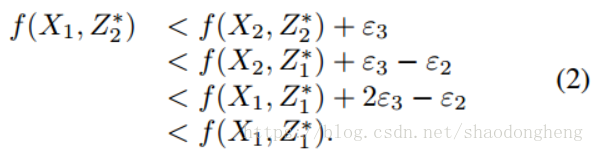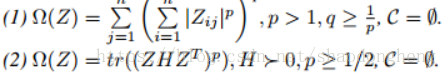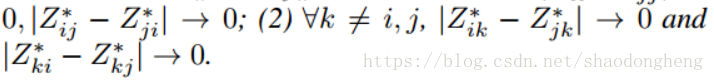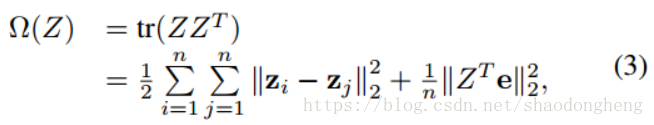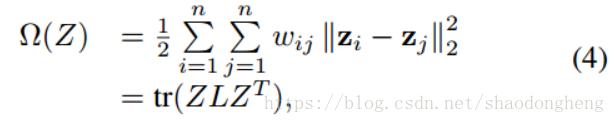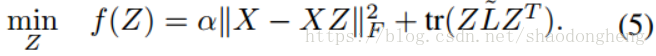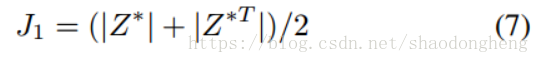Smooth Representation Clustering 翻译

Smooth Representation Clustering 翻译

摘要

子空间聚类是一种用于根据底层子空间聚类数据的强大技术。 基于表示的方法是近年来最流行的子空间聚类方法。 在本文中，我们深入分析了基于表示的方法的分组效果。 特别地，我们引入了强制分组效应条件，这极大地促进了分组效果的分析。 我们进一步发现分组效应对于子空间聚类很重要，子空间聚类应该在数据自我表示模型中明确强制执行，而不是像在某些先前的工作中那样由模型隐含地暗示。 根据我们的分析，我们提出了SMooth Representation（SMR）模型。 我们还提出了一种基于分组效应的新的亲和力度量，证明它比常用的更有效。 因此，我们的SMR在基准数据集中明显优于最先进的方法。

引言

在许多计算机视觉和机器学习问题中，数据可以被视为从多个低维子空间绘制的点，每个子空间对应于一个种类或类别，例如，由仿射相机捕获的移动物体的点轨迹[24]，不同光照或不同姿势下的几个主体[6]的图像，以及图像的像素/超像素的局部斑块或纹理特征[20]。 处理这种数据的基本任务是根据底层子空间聚类点。 这样的任务称为子空间聚类[26]。

相关工作

用于子空间聚类的现有方法可以大致分为三类：基于代数，基于统计和基于谱聚类[26]。

大多数关于子空间聚类的早期研究都是基于代数或统计的。两种最着名的代数方法可能是形状相互作用矩阵（SIM）[2]和广义主成分分析（GPCA）[27]。尽管具有优雅的配方，但通常这些方法的性能在存在噪声，退化或部分耦合的子空间上迅速下降。基于统计的方法将子空间聚类视为混合数据推断问题，因此可以使用来自更一般的统计学习领域的一些流行方法，例如随机样本共识（RANSAC）[5]和期望最大化（EM）[12]。虽然已经开发了几种新技术来改进标准（例如，凝聚性有损压缩（ALC）[22]），模型选择（例如，分支和界限（BB）[10]），但这些方法的性能受到限制他们依赖于估计精确的子空间模型。

最近的许多研究都集中在基于谱聚类的方法[21,30,3,16,29,19,18,17]。这些方法的主要区别在于它们构建亲和力矩阵的方式。直接的方法是从现有的代数方法[21]计算亲和度矩阵，或者通过定义点到子空间或子空间到子空间的距离度量[30]。最近，许多作品应用自我表征的想法来计算亲和力[3,16,29,19,18,17]，即通过其他样本的线性组合来表示每个样本，从而产生最先进的性能。这些方法首先通过求解

来计算自表示矩阵Z *，其中是数据矩阵，每列是样本向量，A（X）是可以学习的字典矩阵或简单地设置为，是一个合适的范数，和分别是Z上的正则化和约束，而α> 0是权衡参数。然后Z *用于计算亲和度矩阵，例如，其进一步输入到谱聚类算法[23]中以产生最终聚类结果。现有方法通过采用不同的正则化项Ω（Z）或约束集来相互区分。表1总结了现有基于表示的方法的的选择，其中是1范数，即所有条目的绝对值之和，是2，1范数，即列向量的2范数之和，是核范数，即，奇异值，是Frobenious范数，即平方项之和的平方根。由于项关注表示错误并且它不是我们论文的主要焦点，我们在后续中使用。

贡献

Lu等人 [18,17]发现最小二乘回归（LSR）[18]和相关自适应子空间分割（CASS）[17]模型都具有如下定义的分组效应。

受[18,17]的启发，我们深入分析了基于表示的方法的分组效应。特别地，我们引入了执行分组效应（EGE）条件，这可以极大地促进基于表示的方法的分组效果的分析。通过EGE条件，我们可以轻松找到具有分组效果的新模型。相比之下，Lu等人 [18,17]以个案的方式证明了LSR和CASS的分组效应。他们的证明是特定的，因此不能应用于其他模型。

我们进一步发现分组效应对于子空间聚类实际上很重要。因此，我们建议在表示模型中明确执行分组效应。相反地，先前的工作[18,17]只是被动地发现LSR和CASS具有分组效应。

最后，根据我们的分析，我们提出了SMooth Representation（SMR）模型。我们还提出了一种基于分组效应的新颖的亲和度量度，证明它比常用量度更有效。我们对基准数据集的实验表明，我们的SMR明显优于最先进的方法。

分组效应

Lu[18,17]等人首先明确说明了分组效应。他们表明，在LSR和CASS中，当样本彼此接近时，它们的表示系数也彼此接近。 他们的证明特定于LSR和CASS，不能应用于其他模型。 在本节中，我们深入分析了基于重建模型的分组效应。 我们首先介绍执行分组效应（EGE）条件，它可以帮助我们轻松识别分组效应。 然后我们研究为什么分组效应有助于子空间聚类。

Enforced Grouping Effect Conditions

我们为分组效应引入一般充分条件如下。

然后我们有以下引理

引理1：如果问题（1）满足EGE条件（1）和（2），则其最优解Z *是X的连续函数。

证明：很明显根据EGE条件（2），Z *可以被认为是X的函数。 在下文中，我们证明了Z * 关于X的连续性。

假设Z *关于X是不连续的，是一个不连续点。我们有

指定因为问题（1）有唯一解，我们有

 根据EGE条件（1），关于X连续：对于任意存在，使所有的 同时存在一些使所有

假设

式（2）表示当时是问题（1）的更好解，这是一个矛盾。 因此Z *关于X的连续性被证明了。

然后我们有以下命题。

命题1：如果满足EGE条件（1），（2）和（3），问题（1）的最优解Z *具有分组效应。

证明：我们首先通过实例化X.考虑中两个足够接近的点和。为简单起见，我们非正式地写表示a和b彼此接近。交换两列和，我们得到一个新的数据矩阵，其中是通过交换单位矩阵的第i列和第j列的置换矩阵。很明显，和。

给定EGE条件（3），很容易检查是唯一的当时问题（1）的最优解。通过引理1，我们得到。因此，作为和仅在第i和第j列不同。

我们现在通过上述EGE条件检查表1中列出的现有基于表示的方法的分组效果。 SSC [3,4]不满足条件。实际上，它没有分组效应。例如，考虑，满足的任何置换矩阵将是SSC的最优解。对于LSR，满足所有EGE条件。所以它具有分组效应。图1（a） - （c）也举例说明了我们的上述观察结果。对于LRR [16,15]，显然满足EGE条件（1）和（3）。如命题2所述，也可以证明LRR最优解的唯一性。因此，LRR具有分组效应。根据[8]，CASS [17]的最优解是唯一的，它也具有分组效应。

命题2：LRR具有唯一最优解。

证明：请在补充材料中找到。

命题1不仅提供了确定现有方法的分组效果的方法，还可以帮助我们设计具有分组效果的新方法。例如，以下方法族具有分组效果。

命题3：当问题（1）有以下Ω（Z）和C时具有分组效应：

证明：请在补充材料中找到。

应该注意的是，约束集，如某些现有方法所使用，如SSC [4]，SSQP [29]，MSR [19]和LSR-Z [18]， 不满足EGE条件（3）。 因此，这些方法严格意义上不具有分组效果。 但是，这些方法也表现良好。 因此，为了符合这样的观察，我们将分组效应的概念概括如下。

定义3（置换分组效应）：给出一个数据点集如果一个自表示矩阵

有置换分组效应，是通过交换单位矩阵的第i行和第j行的置换矩阵。

然后我们有下面的命题。

命题4：如果满足EGE条件（1），（2）和（4），则问题（1）的最优解Z *具有置换分组效应。

证明：类似于命题1的证明，我们形成一个新的数据矩阵。 通过EGE条件（2）和（4），
是当时问题（1）的唯一最优解。 如果，那么通过引理1我们应用得到。
可以检查约束集是否满足EGE条件（4）。 因此，通过命题4，SSQP [29]，MSR [19]和LSR-Z [18]具有置换分组效应。

Why Grouping Effect?

据Lu等人声称 [18] LSR的有效性来自分组效应。但是，在[18]中没有令人信服的证据支持这一说法。在本节中，我们提供了两个视点来为基于表示的方法提倡此属性。

我们首先从优化的角度分析分组效应。问题（1）中的第一项惩罚重建误差，其可被视为编码数据的整个子空间结构的一阶能量。表示矩阵的分组效果表明问题（1）中的Ω（Z）和C必须包括二阶能量，以隐式地或明确地惩罚表示系数中的不连续性。利用这种二阶能量，表示将是稳定的。另一方面，空间上接近的数据点可以互相帮助以防止在重建样本时过度拟合。例如，在图1（a）中，我们考虑由绿色和紫色方块标记的面部。它们外观非常接近，但是大部分被遮蔽，因此违反了子空间约束[6]。 LSR和我们提出的SMooth表示（SMR，参见第3.3节）具有分组效应。它们代表了新空间中的两个面，并且也正确地聚集在一起（图1（b）和（d））。但是，SSC不包括不连续性处罚，使得两个面的表示彼此远离并最终错误地聚集（图1（c））。从亲和力测量的观点来看，最常用的亲和度测量是。通常，分组效应意味着空间上的接近点与其他点具有相似的亲和力。我们在命题5中正式描述了这一点。

命题5：如果满足EGE条件的（1）（2）和（4），对于所有我们有：（1）

证明：根据命题4，我们有，

命题5表明分组效应通常会产生良好平衡的亲和图，这被认为有助于谱聚类[28]。 此外，基于命题5，分组效果使我们能够为子空间聚类定义新的亲和度度量。 我们将证明当自我表示模型具有分组效果时，该亲和度测量比常用的表现更好。

3. Smooth Representation Clustering

在本节中，基于对分组效应的详细分析，我们提出了一种新的子空间聚类方法，称为平滑表示（SMR）聚类。 我们首先介绍如何在表示模型中显式强制执行分组效果，然后介绍SMR模型。

Enforcing Grouping Effect

如2.1节所述，LRR和LSR隐含地使用分组效果。分组效应可以理解为特征对样本的平滑依赖性。我们可以写出LSR的正则化项如下：

其中e是全1向量。可以将其视为为所有表示对分配相等的权重，而不管表示是否彼此接近。通过第2节的分析，我们应该通过样本的亲和力明确地强制执行分组效果。一种可能性是采用以下正则化术语：

其中是测量数据点的空间接近度的权重矩阵，是拉普拉斯矩阵，其中D是具有的对角度矩阵。构造W的常用方法是使用热核或0-1权重[9]的k最近邻（k-nn）图。我们发现简单的0-1加权k-nn图在我们的实验中表现得足够好，如图1（d）所示。因此，我们在所有实验中使用0-1加权k-nn图（k的默认值为4）。还存在更复杂的图，例如，由其他子空间聚类算法产生的亲和图。但是，通常我们没有观察到明显改进k-nn图。

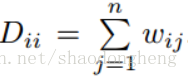
Smooth Representation

为了避免数值不稳定性问题，我们通过添加强制L严格为正定，而，其中I是单位矩阵且0 <ε1。默认值ε为0.01。 然后我们得到我们的平滑表示模型：

问题（5）是平滑的凸程序。 将目标函数f（Z）相对于Z进行微分并将其设置为零，我们得到最优解Z *满足

上面的等式是标准的西尔维斯特方程[1]。 它有一个唯一解。

命题6：西尔维斯特方程（6）有一个唯一解。
证明：是正半正定的。所以它的所有特征值都是非负的：是正定的。所以它的所有特征值都是正的。因此，对于的任何特征值，。根据[14]，西尔维斯特方程（6）有一个唯一解。

Sylvester方程的经典算法是Bartels-Stewart算法[1]，它包括通过QR分解将系数矩阵变换为Schur形式，然后通过反向替换求解得到的三角形系统。该算法具有的计算复杂度。

根据命题7，问题（5​​）的解决方案也具有几个不错的属性。

命题7：问题（5）的解决方案具有以下属性：（1）它具有分组效果; （2）当子空间独立且数据无噪声时，它是块对角线。

证明：（1）我们可以很容易地检查问题（5）是否满足EGE条件（1），（2）和（3）。根据命题1，其解决方案具有分组效应。

（2）当数据矩阵X的列被任何置换矩阵P置换时，我们得到。因此，，其中A和D来自.。将Z和代入等式（4），我们有，其中等式保持当且仅当和。因此Ω（Z）满足强制块对角条件[18]。根据[18]中的定理2，当子空间独立且数据无噪声时，其最优解是块对角线。

此外，受益于分组效应的加强，SMR得出的表示通常在类内和类间距离之间比LRR和LSR具有更大的差距，如定性图1（d）和定量图2所示。这个属性意味着SMR在使用第3.3节中描述的措施时，可以获得与类间相关的更为显着的类内亲和力。

Subspace Clustering by SMR

在获得自表示矩阵Z *之后，子空间聚类的常用方法是将亲和度矩阵定义为

并使用谱聚类算法[23]产生最终的聚类结果，如SSC，LRR和LSR所使用的那样。

J1的有效性主要来自Z *的块对角线性质，使得分组效应的良好性质未被开发。 为了利用分组效果的优点，我们将新的亲和度矩阵定义为

其中> 0用于控制亲和力方差。 新的亲和度量度可以被视为由其原始特征的规范归一化的新表示向量的内积。 归一化防止亲和度测量被原始特征振幅偏置，这在运动分割问题中非常常见，其运动分割问题的轨迹通常在幅度上变化很大。 图3显示了基于SMR导出的Z *的两个度量的亲和度矩阵。 可以看出，J2增强了每个集群内的亲和力，并削弱了集群间的亲和力。 算法1总结了SMR对子空间聚类的整个过程。