A Tutorial on Clustering Algorithms - K-means【翻译】

原文章 A Tutorial on Clustering Algorithms，包含以下部分：

1. ☑ Introduction
2. ☑ Clustering Algorithms
3. ☑ K-means
4. ☒ Fuzzy C-means
5. ☒ Hierarchical
6. ☒ Mixture of Gaussians

本文为 K-means 翻译内容，后续内容请直接点击以上链接（☑为已完成内容）。

本文系Subson翻译，转载请注明。

---

K-means聚类

算法介绍

K-means是最简单的解决众所周知的聚类问题的无监督学习算法之一。通过设定一个必要的族簇数量（假设族簇数量为$k$）作为先验知识可以非常简单而已容易地将给定数据分类。其主要思想是定义$k$个圆心，每个圆心是一个族簇。这些圆心的设置必须非常巧妙，因为不同的位置造成不同的结果。所以，一个好的选择是尽可能的让每一个圆心远离彼此。接下来是让数据集中的每个点和距离其最近的圆心联合起来。当没有数据点处于待分配状态，那么第一步就完成。这时候，我们需要按照前面的步骤重新计算每个族簇的重心作为新的$k$个圆心。有了这$k$个新的圆心，需要重新将数据点和其最近的圆心绑定。循环这个过程，我们可能会注意到这$k$个圆心一步一步改变自己的位置，直到没有改变，便是这个循环的结果。换言之，圆心不再移动。

最终，这个算法的目的是最小化目标函数，即平方差方程。这个目标函数是

$$J=\sum\limits_{j=1}^{k}{\sum\limits_{i=1}^{x}{{{\left\| x_{i}^{\left( j \right)}-{{c}_{j}} \right\|}^{2}}}}$$

其中${\left\|x_{i}^{\left(j\right)}-{{c}_{j}}\right\|}^{2}$是所选择的数据点$x_{i}^{\left(j\right)}$和族簇中心${c}_{j}$之间的距离度量，是各自族簇中心的$n$个数据点的距离指标。

该算法由下列步骤组成：

1. 将$K$个点放入空间作为族簇对象的代表。这些点代表初始的族簇圆心。
2. 将每一个对象分配给其最近的圆心的族簇。
3. 当全部对象分配完毕，重新计算$K$个圆心的位置。
4. 重复第2步和第3步直到圆心不再移动。这种对象分隔使得所采用的度量计算最小化。

尽管它被证明这个过程总是能够停止，K-means算法并不能一定找到最佳结构，即相应的全局目标函数最小解。该算法也对随机初始化族簇中心较为敏感。K-means算法可以多次运行以减小这个影响。

K-means是一个可以适用于多种问题领域的简单算法。正如我们将看到的，它是作用于模糊特征向量的很好的扩展。

示例

假设我们有$n$个全部来自于同一个类别的样本特征向量${x}_{1},{x}_{2},...,{x}_{n}$，并且我们知道其分为$k$个紧凑的族簇（$k<n$）。让${m}_{i}$表示族簇$i$的向量。如果族簇被很好地分隔，我们可以用最小距离分类器分隔它们。这就是说，如果$\left\|x-{m}_{i}\right\|$是所有$k$个距离最小的，那么我们可以说$x$在族簇$i$中。下述程序表示了寻找$k$个均值的过程：

• 初始化均值${x}_{1},{x}_{2},...,{x}_{k}$
• 执行下列步骤直到任何均值不再改变
  
  • 用估计的均值分类样本到各族簇中
  • 从$1$到$k$循环$i$执行下列代码
  • 用族簇$i$的所有样本的均值代替${m}_{i}$
  • 结束循环
• 结束循环

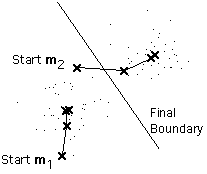
这里有一个例子显示两个族簇的均值${m}_{1}$和${m}_{2}$是如何移动到中心的。

备注

这是简单版的K-means聚类过程。它展示的是以最小化到族簇中心距离的平方和来分隔$n$个样本到$k$个族簇的贪心算法。它有一些缺点：

• 初始化均值的方式不是指定的。一个普遍被接受的方法是随机选择样本的$k$值。
• 该过程的结果取决于均值的初始值，经常产生次优的划分。标准的解决方案是从不同的开始点尝试数值。
• 可能造成最接近族簇中心点${m}_{i}$的样本集合为空，所以${m}_{i}$并不能被更新。这种我们忽略的烦恼在实施过程中必须处理。
• 结果取决于使用的${\left\|x-{m}_{i}\right\|}^{2}$度量。一个被普遍采用的方案是通过标准差去标准化每个变量，尽管这种方法并不是总令人满意。
• 结果取决于$k$的值。

最后一个问题特别麻烦，即我们经常没有途径知道有多少个族簇存在。如上面的例子所示，采用同样的算法遵循3个均值的聚类应用于同样的数据，得到的结果相较于2个均值的聚类孰好孰坏？

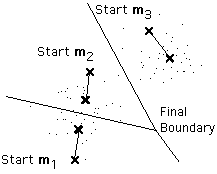
不幸的是没有一般理论化的解决方案用于找到任何给定数据集的最佳族簇数量。一个简单的方法是比较采用不同$k$值多次运行的结果，根据给定的准则（比如施瓦茨准则）去选择最好的，但是我们不仅得谨慎于在较小的定义误差函数的值的允许范围内增大$k$值，还得谨慎过拟合增大的风险。

后续章节待续。。。

---

本文系Subson翻译，转载请注明。