有一种组合方向的考虑有没有dalao肯高抬啊?
题目大意
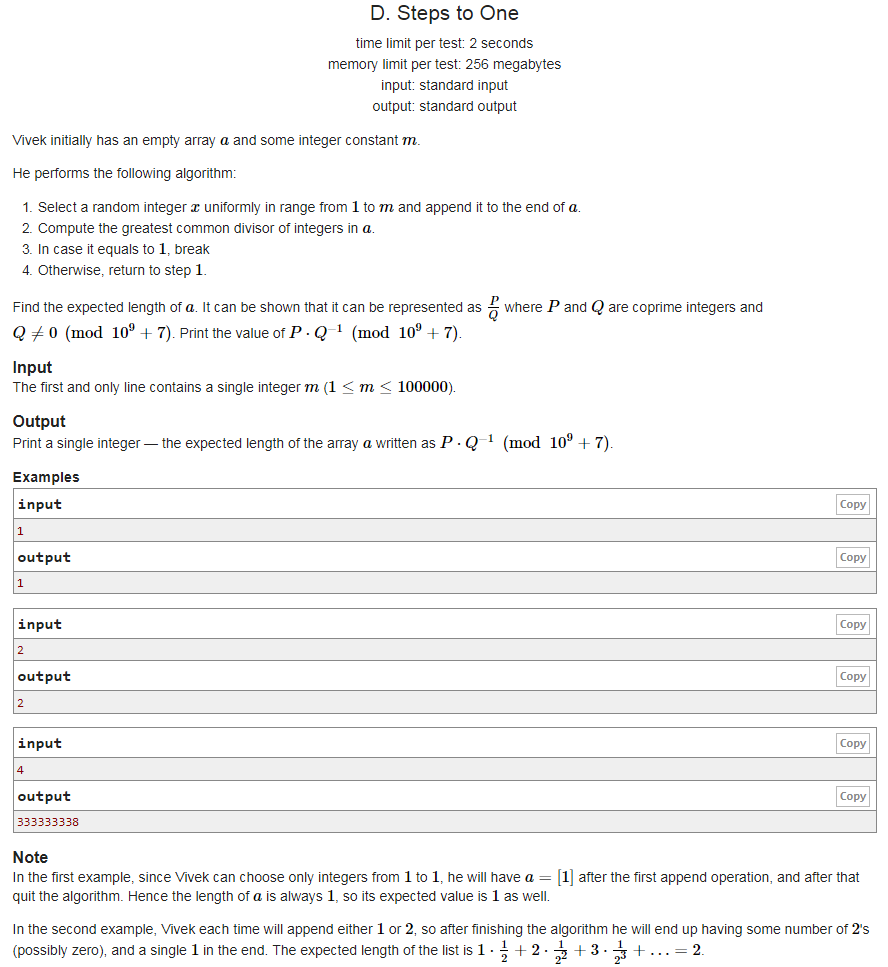
有一个初始为空的数组$a$,按照以下的流程进行操作:
- 在$1\cdots m$中等概率选出一个数$x$并添加到$a$的末尾
- 如果$a$中所有元素的$\gcd=1$则完成这个数组$a$的修改
- 重复这一过程
求数组$a$的期望长度,$m \le 10^5,\mod 10^9+7$
题目分析
质因数分解的期望dp题
以下介绍的两个做法中,第一个做法本人不会所以 求助会做的dalao麻烦高抬一手 ;
第二个做法是对推得的dp式子质因数分解求解————当然网上更多的是莫比乌斯反演的做法,此处就不介绍了。
未完的做法一:组合考虑
考虑计算$f(d)$为:数组$a$的前$len-1$个(也即结束前的那一序列)$\gcd=d$时,对答案的期望长度贡献。
那么枚举结束前的长度$i$,记$h(d)$为$1\cdots m$中与$d$互质的数的个数;$g(i,d)$为一个$\gcd=d$的长度为$i$的序列的概率,有$f(d)=\sum\limits_{i=1}^{∞}(i+1)\times g(i,d)\times h(d)$。
当然,这样的式子远远不够。$h(d)$的计算非常轻松但是问题在于$g(i,d)$有没有什么组合上的表达方式。我最初以为$g(i,d)=\lfloor\frac{m}{d}\rfloor^{i-1}\times \frac{1}{m}$,意即将序列看做是无序取入的集合,确保$i-1$个元素都是$\{d,2d,3d\cdots\}$,并钦点一个$d$.但是这个处理有两个问题:1.序列不能够这样看成无序集合;2.并不是必须要有一个$d$才能使数组的$\gcd=d$,例如$\{2d,3d,5d\}$就有$\gcd=d$。
这个方向大概不太能行吧,为求出式子,$g(i,d)$可能还有更严苛的表达限制。
做法二:质因数分解
由于这里的长度是无穷的,所以处理角度还当是从序列的$\gcd$入手。
记$f_d$为当前数组已经$\gcd=d$,到达$\gcd=1$的状态的期望步数。(这个状态要比我上面那个状态要优秀地多)
容易得到转移$f_d=1+\frac{1}{m} \sum\limits_{i=1}^mf_{\gcd(i,d)}$,
稍作化简得到$f_d=1+\frac{1}{m} \sum\limits_{i\mid d,i\ne d}(f_i\times c(i,d)+\lfloor\frac{m}{d}\rfloor f_d)$,其中$c(i,d)=\sum\limits_{j=1}^m[\gcd (d,j)=i]$.