1. 梯度下降法

梯度下降法用来求解目标函数的极值。这个极值是给定模型给定数据之后在参数空间中搜索找到的。迭代过程为：
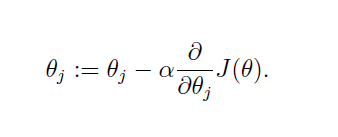
在这里插入图片描述
可以看出，梯度下降法更新参数的方式为目标函数在当前参数取值下的梯度值，前面再加上一个步长控制参数alpha。梯度下降法通常用一个三维图来展示，迭代过程就好像在不断地下坡，最终到达坡底。为了更形象地理解，也为了和牛顿法比较，这里我用一个二维图来表示：
在这里插入图片描述懒得画图了直接用这个展示一下。在二维图中，梯度就相当于凸函数切线的斜率，横坐标就是每次迭代的参数，纵坐标是目标函数的取值。每次迭代的过程是这样：

首先计算目标函数在当前参数值的斜率（梯度），然后乘以步长因子后带入更新公式，如图点所在位置（极值点右边），此时斜率为正，那么更新参数后参数减小，更接近极小值对应的参数。
如果更新参数后，当前参数值仍然在极值点右边，那么继续上面更新，效果一样。
如果更新参数后，当前参数值到了极值点的左边，然后计算斜率会发现是负的，这样经过再一次更新后就会又向着极值点的方向更新。

根据这个过程我们发现，每一步走的距离在极值点附近非常重要，如果走的步子过大，容易在极值点附近震荡而无法收敛。解决办法：将alpha设定为随着迭代次数而不断减小的变量，但是也不能完全减为零。

在使用梯度下降时，需要进行调优。哪些地方需要调优呢？

算法的步长选择。步长取值取决于数据样本，可以多取一些值，从大到小，分别运行算法，看看迭代效果，如果损失函数在变小，说明取值有效，否则要增大步长。步长太大，会导致迭代过快，甚至有可能错过最优解。步长太小，迭代速度太慢，很长时间算法都不能结束。所以算法的步长需要多次运行后才能得到一个较为优的值。
算法参数的初始值选择。初始值不同，获得的最小值也有可能不同，因此梯度下降求得的只是局部最小值；当然如果损失函数是凸函数则一定是最优解。由于有局部最优解的风险，需要多次用不同初始值运行算法，关键损失函数的最小值，选择损失函数最小化的初值。
归一化。由于样本不同特征的取值范围不一样，可能导致迭代很慢，为了减少特征取值的影响，可以对特征数据归一化。

2. 牛顿法

一般来说，牛顿法主要应用在两个方面，1：求方程的根；2：最优化。

2.1 求方程的根

在这里插入图片描述所以求根的牛顿迭代方程为：

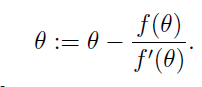
2.2 最优化

如果要求解f(x)的极值呢？很简单，牛顿迭代方程稍微做下改动即可：
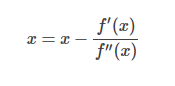
在这里插入图片描述
上述所讲的迭代方法都是一维简单情形下的，接下来就推广牛顿迭代法在多维的情况。
例子：

代码：

"""
Newton法
Rosenbrock函数
函数 f(x)=100*(x(2)-x(1).^2).^2+(1-x(1)).^2
梯度 g(x)=(-400*(x(2)-x(1)^2)*x(1)-2*(1-x(1)),200*(x(2)-x(1)^2))^(T)
"""

import numpy as np
import matplotlib.pyplot as plt

def jacobian(x):
    return np.array([-400*x[0]*(x[1]-x[0]**2)-2*(1-x[0]),200*(x[1]-x[0]**2)])

def hessian(x):
    return np.array([[-400*(x[1]-3*x[0]**2)+2,-400*x[0]],[-400*x[0],200]])

X1=np.arange(-1.5,1.5+0.05,0.05)
X2=np.arange(-3.5,2+0.05,0.05)
[x1,x2]=np.meshgrid(X1,X2)
f=100*(x2-x1**2)**2+(1-x1)**2; # 给定的函数
plt.contour(x1,x2,f,20) # 画出函数的20条轮廓线


def newton(x0):

    print('初始点为:')
    print(x0,'\n')
    W=np.zeros((2,10**3))
    i = 1
    imax = 1000
    W[:,0] = x0 
    x = x0
    delta = 1
    alpha = 1

    while i<imax and delta>10**(-5):
        p = -np.dot(np.linalg.inv(hessian(x)),jacobian(x))
        x0 = x
        x = x + alpha*p
        W[:,i] = x
        delta = sum((x-x0)**2)
        print('第',i,'次迭代结果:')
        print(x,'\n')
        i=i+1
    W=W[:,0:i]  # 记录迭代点
    return W

x0 = np.array([-1.2,1])
W=newton(x0)

plt.plot(W[0,:],W[1,:],'g*',W[0,:],W[1,:]) # 画出迭代点收敛的轨迹
plt.show()

输出结果：

初始点为:
[-1.2  1. ] 

第 1 次迭代结果:
[-1.1752809   1.38067416] 

第 2 次迭代结果:
[ 0.76311487 -3.17503385] 

第 3 次迭代结果:
[ 0.76342968  0.58282478] 

第 4 次迭代结果:
[ 0.99999531  0.94402732] 

第 5 次迭代结果:
[ 0.9999957   0.99999139] 

第 6 次迭代结果:
[ 1.  1.]

即迭代了6次得到了最优解，画出的迭代点的轨迹如下：
在这里插入图片描述有关牛顿法的推倒：