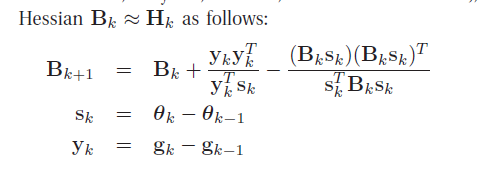转载请注明出处:勿在浮沙筑高台http://blog.csdn.net/luoshixian099/article/details/51821460
无约束优化问题是机器学习中最普遍、最简单的优化问题。
1.梯度下降
梯度下降是最简单的迭代优化算法,每一次迭代需求解一次梯度方向。函数的负梯度方向代表使函数值减小最快的方向。它的思想是沿着函数负梯度方向移动逐步逼近函数极小值点。选择适当的初始值
固定学习率
梯度下降伪代码(固定学习率):
1. 取初始值x(0) ,令k=0,学习率α ,容忍度ϵ ;
2. 计算梯度gk=▽x(k) ,若|gk|<ϵ ,则停止迭代,返回x∗=x(k) ;
3. 更新x(k+1)=x(k)−αgk ,若|x(k+1)−x(k)|<ϵ 或者|f(x(k+1))−f(x(k))|<ϵ ,则停止迭代,返回x∗=x(k+1)
4. k=k+1,转到步骤2
值得一提的是梯度下降算法与下面介绍的几种算法都不能保证函数能降低到全局最小值附近,有可能是局部最小值附近。如果目标函数
下图是二维函数
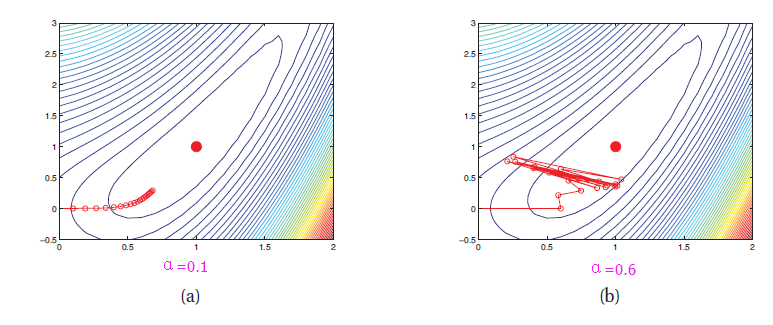
上图中学习率
线性搜索
固定学习率中每一迭代更新
梯度下降伪代码(线性搜索):
1. 取初始值x(0) ,令k=0,学习率α ,容忍度ϵ ;
2. 计算梯度gk=▽x(k) ,若|gk|<ϵ ,则停止迭代,返回x∗=x(k) ;
3. 计算αk=minαh(α)=minα f(xk−αgk)
4.更新x(k+1)=x(k)−αkgk ,若|x(k+1)−x(k)|<ϵ 或者|f(x(k+1))−f(x(k))|<ϵ ,则停止迭代,返回x∗=x(k+1)
5. k=k+1,转到步骤2
采用线性搜索:

注意到线性搜索的迭代相邻轨迹垂直,如图(b)。这是由于取
一种减弱上述相互垂直轨迹的方法是添加一个动量项(momentum term):
2.牛顿法
假设f(x)具有二阶连续偏导数,在
其中
牛顿法利用极小点的必要条件
化简得:
伪代码:

实际上可以把f(x)在
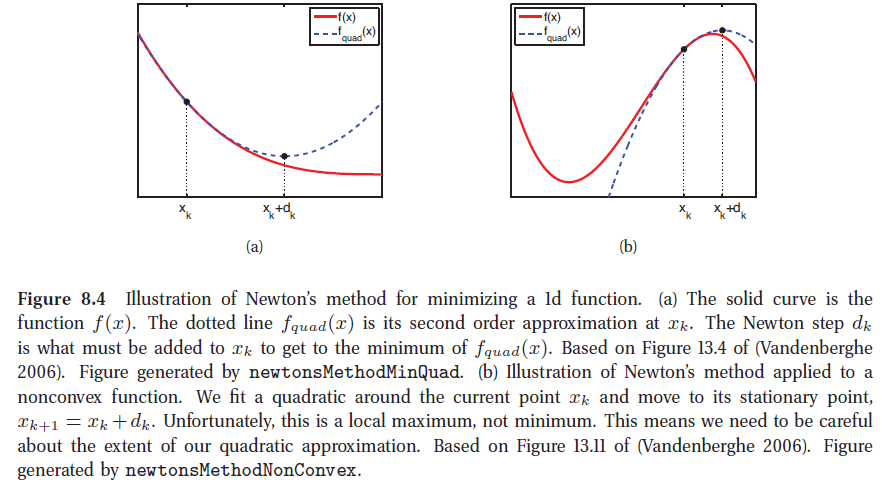
牛顿法一个问题是
Hk 可能不是正定矩阵(f(x)非凸),计算出的pk 牛顿方向错误,图(b)的情况。针对图(b)的非凸函数,可以采用梯度下降与牛顿法结合使用,即当牛顿方向与负梯度方向夹角小于90度时,采用牛顿方向,否则采用负梯度方向。
3.拟牛顿法
牛顿法中需要计算Hessian矩阵的逆,往往计算量非常大,所以提出拟牛顿方法采用矩阵近似
采用一个不断迭代的矩阵
BFGS伪代码:
1. 取初始值x(0) ,令k=0,学习率α ,容忍度ϵ,B0=I ;
2. 计算梯度gk=▽x(k) ,若|gk|<ϵ ,则停止迭代,返回x∗=x(k) ;
3. 由Bkpk=−gk ,计算出拟牛顿方向pk ;
3. 计算αk=minαh(α)=minα f(xk+αpk) ;
4. 更新x(k+1)=x(k)−αkpk 与Bk+1 ,若|x(k+1)−x(k)|<ϵ 或者|f(x(k+1))−f(x(k))|<ϵ ,则停止迭代,返回x∗=x(k+1) ;
5. k=k+1,转到步骤2
Reference:
统计学习方法.李航
Machine Learning A Probabilistic Perspective.Kevin P. Murphy