从梯度下降法、牛顿法到拟牛顿法，浅谈它们的联系与区别

考虑一个求多元函数 $\mathbb{f}(\pmb{x})$求最小值的问题，当我们无法求出精确结果时，需要使用一些算法求出它的数值解，本文主要探讨基于梯度的优化算法中比较常见的三种算法：梯度下降法、牛顿法和拟牛顿法。

1.梯度下降法

在说梯度下降法之前，概念首先说说梯度的概念：梯度是相对一个向量求导的导数，它的定义为 $\triangledown_xf(\pmb{x})=\left(\frac{\partial f}{\partial x_1},\cdots,\frac{\partial f}{\partial x_n}\right)$。事实上，对于任意一个单位向量 $\pmb{u}$， $\mathbb{f}(\pmb{x})$在 $\pmb{u}$方向上的方向导数为 $\frac{\partial f(\vec{x}+\alpha\vec{u})}{\partial \alpha}|_{\alpha=0}=\pmb{u}^T\triangledown_xf(\pmb{x})$,由柯西不等式可知 $\pmb{u}^T\triangledown_xf(\pmb{x})\le\|\pmb{u}\|_2\|\triangledown_xf(\pmb{x})\|_2$,当 $\pmb{u}$和 $\triangledown_xf(\pmb{x})$同方向时取等号。从以上的分析可以看出梯度的意义：函数在梯度方向上的方向导数最大，换言之即函数沿着梯度方向上升的速度最快。梯度下降法基于这个原理，既然沿着梯度方向上升最快，那么梯度的反方向就是下降最快的方向（ $\pmb{u}^T\triangledown_xf(\pmb{x})\ge-\|\pmb{u}\|_2\|\triangledown_xf(\pmb{x})\|_2$,当 $\pmb{u}$和 $\triangledown_xf(\pmb{x})$方向相反时取等号）,所以只要沿着负梯度的方向上移动就可以减小 $f$，具体而言，梯度下降法在每一步的迭代中使用如下算法：
$\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\pmb{x}_{k+1}=\pmb{x}_k-\varepsilon\triangledown_xf(\pmb{x}_k)$
其中 $\varepsilon$为学习率，是一个确定步长的正标量。确定步长 $\varepsilon$的方法之一就是计算 $f(\pmb{x}-\varepsilon\triangledown_xf(\pmb{x}))$并选择其中能产生最小目标函数值的 $\varepsilon$。梯度下降法的优点是思路简单，计算方便，由普通梯度下降法经过改进的随机梯度下降更是一种针对大样本集的高效学习算法，然而，梯度下降法同样存在一些问题，例如，一个函数如果方向导数在某些方向上增加得很快，而在另一些方向上增加得很慢，由于梯度下降法只考虑了某一点处方向导数的大小而没有考虑他们的变化率，所以它不知道优先探索那些方向导数长期为负的方向，就好比公司招人时只考虑了应聘者的当下水平却没有他们的发展潜力，这样导致的后果是：看似每一步都选择了下降最快的方向，但实际整个下降路径可以一条反反复复的折线，如图

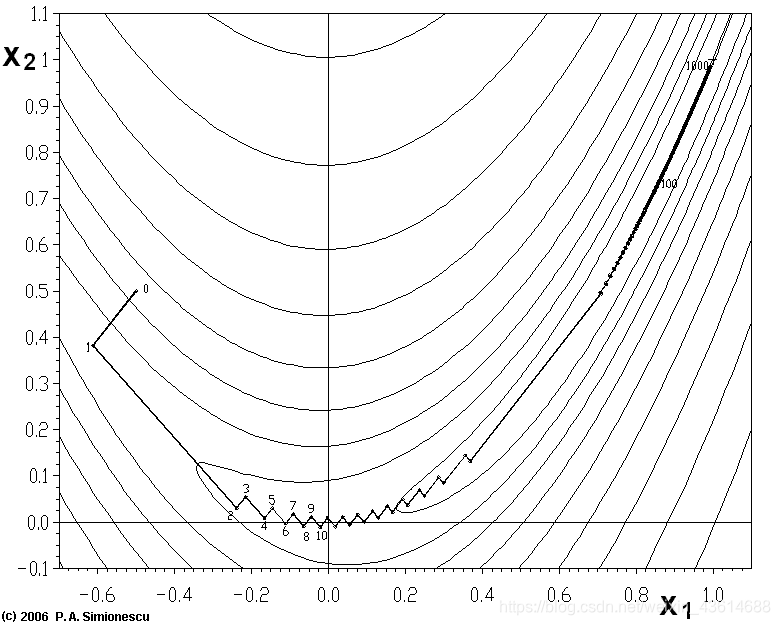
此外梯度下降中关于步长的选择也是一个问题，如果选择太小，受敛速度会很慢，如果太大又容易跳过极小值点，造成反复搜索。
关于步长的计算，可以考虑用函数的二阶泰勒展开近似代替原函数： $f(\pmb{x}-\varepsilon g)=f(\pmb{x})-\varepsilon g^{T}g+\frac{1}{2} g^{T}Hg$,在极小值附近Hessian矩阵是正定的，于是最优步长为 $\varepsilon^*=\frac{g^Tg}{g^THg}$ 。

2.牛顿法

梯度下降法仅利用了梯度信息，属于一阶优化算法，而牛顿法综合考虑了梯度和梯度的变化率信息，属于二阶优化算法。在第一部分计算步长时，使用了二阶泰勒展开近似代替原函数，那么选择最优步长的计算实际上是求解优化问题： $\min\limits_{\vec{x}} \left[f(\pmb{x}_0)+(\pmb{x}-\pmb{x}_0)^T\triangledown_xf(\pmb{x}_0)+\frac{1}{2}(\pmb{x}-\pmb{x}_0)^T H(\pmb{x}-\pmb{x}_0)\right]\text{subject to}\space\pmb{x}-\pmb{x}_0=\varepsilon\pmb{g}$
其中 $\pmb{g}$为 $\mathbb{f}(\pmb{x})$在 $\pmb{x}_0$处的梯度，那么牛顿算法相当于去掉约束条件，直接求解优化问题：
$\min\limits_{\vec{x}} \left[f(\pmb{x}_0)+(\pmb{x}-\pmb{x}_0)^T\triangledown_xf(\pmb{x}_0)+\frac{1}{2}(\pmb{x}-\pmb{x}_0)^T H(\pmb{x}-\pmb{x}_0)\right]$
根据计算结果结果自主的选择最小值的搜索方向，通过计算可知，当 $\pmb{x}-\pmb{x}_0=-H^{-1}\triangledown_xf(\pmb{x})$时，上述优化问题取得最小值。所以，牛顿法迭代过程中的更新步骤为：
$\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\pmb{x}_{k+1}=\pmb{x}_k-H^{-1}\triangledown_xf(\pmb{x}_k)$
将这个式子带入 $f(\pmb{x}_{k+1})=f(\pmb{x}_k)+(\pmb{x}_{k+1}-\pmb{x}_k)^T\triangledown_xf(\pmb{x}_k)+\frac{1}{2}(\pmb{x}_{k+1}-\pmb{x}_k)^T H(\pmb{x}_{k+1}-\pmb{x}_k)$可以得到： $f(\pmb{x}_{k+1})=f(\pmb{x}_k)-\frac{1}{2}g^TH^{-1}g$显然要使牛顿法每一步迭代都是下降的，Hessian矩阵 $H$必须为正定矩阵，这样就要求迭代时距离起始点最近的临界值点为极小值点，这样也可以保证下降过程中不会被吸引到拐点。
如果 $f$本身就是一个正定二次函数，牛顿法经过一次迭代就能达到它的最小值，若使用梯度下降法，可能需要迭代多次。通过这个例子可以看出，牛顿法比梯度下降法更快的收敛到极小值。但是牛顿法存在一个严重的问题：对于一个复杂的函数，如果每一步都计算Hessian矩阵的逆矩阵将会造成很大的开销，尤其是对于数据维度比较高的问题。

3.拟牛顿法

既然梯度下降法存在收敛慢的问题，而牛顿法又存在开销大的问题，那么人们就思考能否找到一种收敛速度快开销有相对较小的方法，于是，拟牛顿法就横空出世了。
拟牛顿法的思路是：每一步迭代的更新步骤选择 $\pmb{x}_{k+1}=\pmb{x}_k-\varepsilon G_k\triangledown_xf(\pmb{x}_k)$,其中 $G_k\triangledown_xf(\pmb{x}_k)$为搜索方向， $\varepsilon$为学习率，用 $\mathbb{f}(\pmb{x})$的一阶泰勒展开式近似代替原函数并将迭代更新公式带入其中得 $f(\pmb{x}_{k+1})=f(\pmb{x}_k)-\varepsilon (\triangledown_xf(\pmb{x}_k))^TG_k\triangledown_xf(\pmb{x}_k)$,要使每一步迭代函数值都下降，则 $G_k$必须是正定矩阵。下面的问题就在于确定每一步的 $G_k$,即确定每一步的搜索方向。牛顿法中搜索方向的选择考虑了每一步的梯度变化率，基于这个思路，拟牛顿法将每一步的梯度变化率作为 $G_k$的更新依据，即置 $\pmb{x}_{k+1}-\pmb{x}_{k}=G_{k+1}\left[\triangledown_xf(\pmb{x}_{k+1})-\triangledown_xf(\pmb{x}_k)\right]$,记 $v_k=\triangledown_xf(\pmb{x}_{k+1})-\triangledown_xf(\pmb{x}_k)$, $w_k=\pmb{x}_{k+1}-\pmb{x}_{k}$,则 $w_k=G_{k+1}v_k$,关于 $G_{k+1}$的选择有多种方法，以DFP算法为例，它假设每一步迭代中 $G_{k+1}$是由 $G_k$加上两个附加项组成，即 $G_{k+1}=G_k+P_k+Q_k$,其中 $P_k,Q_k$是待定矩阵,这时：
$\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space G_{k+1}v_k=G_kv_k+P_kv_k+Q_kv_k$
为使 $G_{k+1}$满足条件，可使
$\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space P_{k}v_k=w_k$
$\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space Q_{k}v_k=-G_kv_k$
例如取
$\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space P_{k}=\frac{w_kw_k^T}{w_k^Tv_k}$
$\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space Q_{k}=-\frac{G_kv_kv_k^TG_k}{v_k^TG_kv_k}$
于是
$\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space G_{k+1}=G_k+\frac{w_kw_k^T}{w_k^Tv_k}-\frac{G_kv_kv_k^TG_k}{v_k^TG_kv_k}$
在极小值点附近（Hessian矩阵正定），只要初始矩阵 $G_0$是正定的，则所有的 $G_k$都是正定的。可以用数学归纳法证明这一点：假设 $G_k$正定,则存在正定对称矩阵 $P$使得： $G_k=P^TP$，将函数二阶泰勒展开可得： $w_k^Tv_k=v_k^TH_k^{-1}v_k$，于是
$\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space G_{k+1}=P^T\left(I+\frac{Q^Tw_kw_k^TQ^{-1}}{v_k^TH_k^{-1}v_k}-\frac{Pv_kv_k^TP^T}{v_k^TP^TPv_k}\right)P$
其中 $Q=P^{-1}$,要证明 $G_{k+1}$正定，只需要证明括号里面的矩阵正定即可。令 $M=I-\frac{Pv_kv_k^TP^T}{v_k^TP^TPv_k}$, $N=\frac{Q^Tw_kw_k^TQ}{v_k^TH_k^{-1}v_k}$, $O=I+\frac{Q^Tw_kw_k^TQ}{v_k^TH_k^{-1}v_k}-\frac{Pv_kv_k^TP^T}{v_k^TP^TPv_k}$,则 $O=M+N$.显然 $N$是半正定的，通过计算有 $M^2=M,M^T=M$,且 $tr(M)=n-1$。所以， $M$是半正定矩阵，其零特征值对应的特征空间是一维的，对应的特征向量为 $kPv_k,k\in\mathbb{Z}$.对任意非零向量 $\pmb{y}$,如果 $\pmb{y}\neq kPv_k$,则
$\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\pmb{y}^TO\pmb{y}\ge \pmb{y}^TM\pmb{y}>0$
若 $\pmb{y}= kPv_k$,则
$\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\pmb{y}^TO\pmb{y}= \pmb{y}^TN\pmb{y}=k^2v_k^TH_k^{-1}v_k>0$
综上， $O$是正定矩阵，所以 $G_{k+1}$是正定矩阵，证毕。
通过整个过程可以看出，拟牛顿法实际上是用了一个正定矩阵来代替Hessian矩阵的逆矩阵，这样不仅拥有较快的收敛速度，而且通过一步步迭代更新大大减少了计算开销。拟牛顿算法对于训练集不是很大的机器学习优化问题而言是一种十分高效的算法，学习率 $\varepsilon$的确定方法完全类似于梯度下降法中学习率的确定方法。