一、相关概念
深度前馈网络,也叫作前馈神经网络或者多层感知机。
前馈网络的目标是近似某个函数f*(x)。
这种模型被称为前向的,是因为在模型的输出和模型本身之间没有反馈连接。
前馈神经网络之所以被称作网络,是因为它们通常用许多不同函数复合在一起来表示。例如,有三个函数f1,f2,f3连接在一个链上形成f(x)=f3(f2(f1(x))),链的全长称为模型的深度,前馈网络的最后一层被称为输出层。
每个样本x都伴随这一个标签y≈f*(x),训练样本直接指明了输出层在每一点x上必须做什么;它必须产生一个接近y的值。但是训练数据并没有直接指明其他层应该怎么做。学习算法必须决定如何使用这些层来产生想要的输出,但是训练数据并没有说每个单独的层应该做什么。因为训练数据并没有给出这些层中的每一层所需的输出,所以这些层被称为隐藏层。
二、XOR函数
线性模型不能用来表示XOR函数,如图所示,不能画一条线把0和1分开:

引入一个非常简单的前馈神经网络:一个隐藏层,一个输出层,共两层。
这个前馈网络有一个通过函数f1计算得到的隐藏单元的向量h。这些隐藏单元的值随后被用作第二层的输入。第二层就是这个网络的输出层。输出层仍然只是一个线性回归模型,只不过现在它作用于h而不是x。

我们必须用非线性函数来描述这些特征。大多数神经网络通过仿射变换之后紧跟着一个被称为激活函数的固定非线性函数来实现这个目标。这里我们使用这种策略,定义:
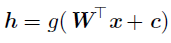
其中W是线性变换的权重矩阵,c 是偏置。在现代神经网络中,默认的推荐是使用由激活函数g(z) = max{0,z}定义的整流线性单元。现在,可以指明整个网络是:
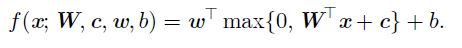
我们现在可以给出XOR 问题的一个解。令:

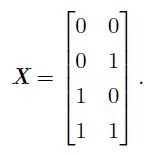
代入计算后,得到的h向量为:
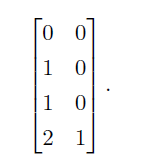
如图所示,它们现在处在一个可以用线性模型解决的空间上:

最后乘以一个权重向量w得到了XOR函数的正确结果: