如何理解递归?
举个例子,周末你带着女朋友取电影院看电影,女朋友问你,咋们闲杂坐在第几排?电影院里面太黑了,看不清,没法数,现在那你怎么办?
你可以问前面一排的人他是第几排,你想只要在他的数字上加上,就知道自己在哪一排了。但是,前面的人也看不清,所以它也问前面的人,就这样一排排往前问,直到问到第一排的人,说我在第一排,然后再这样一排一排再把数字传过来。
这就是一个非常标准的递归求解问题的分解过程,去的过程是“递”,回来的过程是“归”。基本上,所有的递归问题都可以用递推公式来表示:
f(n)=f(n-1)+1 其中,f(1)=1
在知道了递推公式之后,就可以很容易地翻译出代码了:
int f(int n){
if(n==1) return 1;
return f(n-1) + 1;
}递归需要满足的三个条件
1.一个问题的解可以分解为几个子问题的解
子问题,就是数据规模更小的问题。
2.这个问题和分解之后的子问题,除了数据规模不同,求解思路完全一样
比如前面电影院的例子,求解自己在哪一排的思路,和前面一排求解“自己在哪一排”的速录是一摸一样的。
3.存在终止条件
不能无限递归,一定要存在终止条件。
如何编写递归代码?
写递归代码最关键的是写出递推公式,找到终止条件。剩下把递推公式转化为代码就很简单了。
举个例子,假设我们有n个台阶,每一次可以跨1或者2个台阶。请问走这n个台阶有多少种走法?如果有7个台阶,你可以2,2,2,1这样子上去,也可以1,2,1,1,2这样子上去,总之走法有很多。其实,我们仔细想下,实际上,可以根据第一步的走法把所有走法分为两类,第一类是第一步走了1个台阶,另一类是第一步走了2个台阶。所以n个台阶的走法就等于先走1阶后,n-1个台阶的走法加上先走2阶后,n-2个台阶的走法。用公式来表示就是:
f(n) = f(n-1)+f(n-2)
有了递推公式,那么只剩下终止条件。当有一个台阶的时候,我们就不需要再递归了,就只有一种走法,所以f(1) = 1。当只剩2个台阶,有两种走法,一是一步一步走,另外一种是一次性两步。所以有f(2) = 2。所以递归的终止条件就是:f(1) = 1,f(2) = 2。
我们把递推公式和终止条件放在一起就是这样:
f(1) = 1;
f(2) = 2;
f(n) = f(n-1)+f(n-2)
对于递归代码,这种试图想清楚整个递和归过程的做法,实际上是进入了一个思维误区。很多时候,我们理解起来比较吃力,主要原因就是自己给自己制造了这种理解障碍。那正确的思维方式应该是怎么样的呢?
如果一个问题可以分解成若干子问题B、C、D,你可以假设子问题BCD已经解决,在此基础上思考如何解决问题A。而且,你只需要思考问题A与子问题BCD两层之间的关系就可以了,不需要一层一层往下思考子问题与子子问题,子子问题与子子子问题之间的关系。屏蔽掉递归细节,这样子理解起来就简单很多了。
递归代码要警惕堆栈溢出
在实际的软件开发中,编写递归代码的时候,我们可以会遇到堆栈溢出。而堆栈溢出会造成系统崩溃,后果很严重。
我们在“栈”那一节讲过,函数调用会使用栈来保存临时变量。每调用一个函数,都会将临时变量封装为栈帧压入内存栈,等函数执行完成返回的时候,才出栈。系统栈或者虚拟机栈空间都不大。如果递归求解的数据规模很大,调用层次很深,一直压入栈,就会出现堆栈溢出的风险。
那么,如何避免出现堆栈溢出?
我们可用通过在代码中限制递归调用的最大深度的方式来解决这个问题。递归调用超过一定深度,我们就不再继续往下递归了。
// 全局变量,表示递归的深度。
int depth = 0;
int f(int n) {
++depth;
if (depth > 1000) throw exception;
if (n == 1) return 1;
return f(n-1) + 1;
}
但这种做法并不能完全解决问题,因为最大允许的递归深度跟当前线程剩余的栈空间大小有关,事先无法计算。如果实时计算,代码过于复杂,就会影响代码的可读性。所以,如果最大深度比较小,比如10,50,就可以使用这种方法,否则这种方法并不是很实用。
递归代码要警惕重复计算
除此之外,使用递归还会出现重复计算的问题。刚在将的递归代码的例子,如果我们把整个递归过程分解一下的话,那就是这样的:
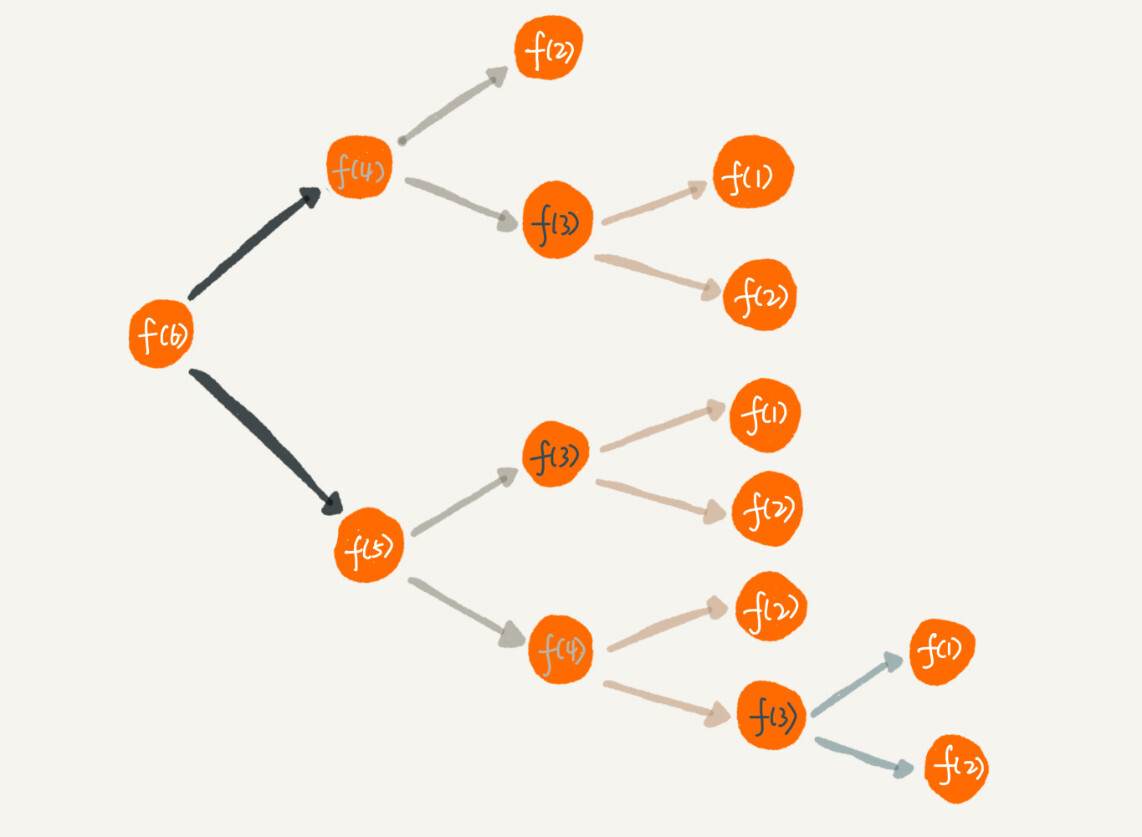
从图中,我们可以看到,想要计算f(5),需要先计算f(4)和f(3),而计算f(4)还需要计算f(3),因此f(3)就被计算了很多次。这就是重复计算问题。
为了避免重复计算,我们可以通过散列表来保存已经求解过的f(k),当递归调用f(k)时,先看下是否已经求解过了。如果是,则直接从散列表中取值返回,不需要重复计算。
如何借助树来求解递归算法的时间复杂度?
我们前面讲过,递归的思想就是,将大问题分解为小问题来求解,然后再将小问题分解成小小问题。这样一层一层地分解,直到问题的数据规模被分解得足够小,不用继续递归分解为止。
如果我们把这个一层一层的分解过程画成图,它其实就是一棵树。我们给这棵树起一个名字,叫做递归树。比如斐波拉契数列:
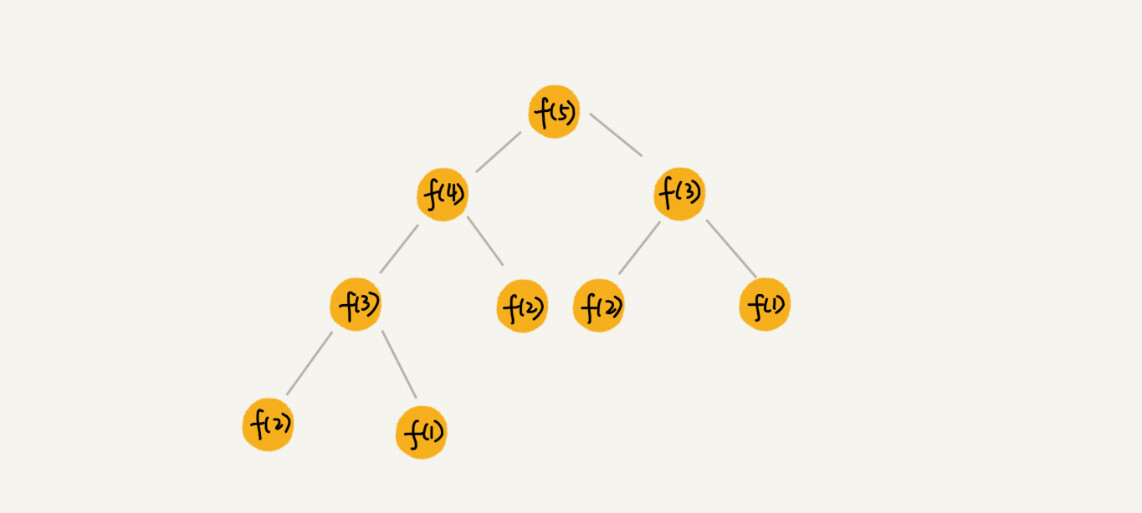
我们来分析归并排序的时间复杂度:
归并排序每一次都将数据规模一分为二,我们画成递归树,就是下面这样子:
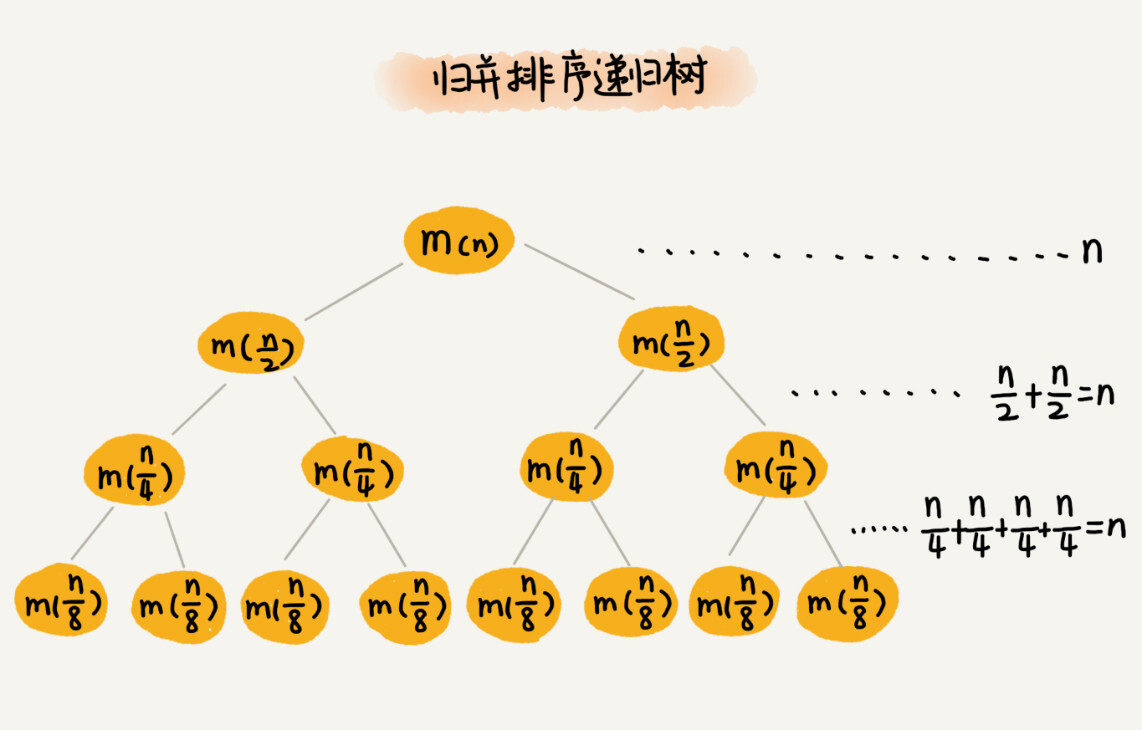
因为每次分解都是一分为二,所以代价很低。我们把时间上的消耗记作常量1。归并算法中比较耗时的是归并操作,也就是把两个子数组合并为大数组。从图中我们可以看出,每一层归并操作消耗的时间总和是一样的,跟要排序的数据规模有关。我们把每一层归并操作消耗的时间记作n。
现在,我们只需要直到这棵树的高度h,用高度h乘以每一层的时间消耗n,就是总的时间复杂度O(n*h)。
从归并排序的原理和递归树,可以看出来,归并排序递归树其实是一颗满二叉树。所以高度是O(log2n) ,所以归并排序的时间复杂度就是O(nlog2n)。
1.分析快速排序的时间复杂度
在用递归推导之前,我们先来回忆一下用递推公式的分析方法。快速排序在最好情况下,每次分区都能一分为二,这个时候用递推公式T(n) = 2T(n/2) + n,很容易就能推导出时间复杂度是O(nlogn)。但是,我们并不可能每次分区都这么幸运,正好一分为二。
我们假设平均情况下,每次分区之后,两个分区的大小比例为1:k。当k = 9时,如果用递推公式的方法来求解时间复杂度的话,递推公式就写成看T(n) = T(n/10) + T(9n/10) +n。这个公式可以推导出时间复杂度,但是推导过程非常复杂,我们试一下用递归树来求解。
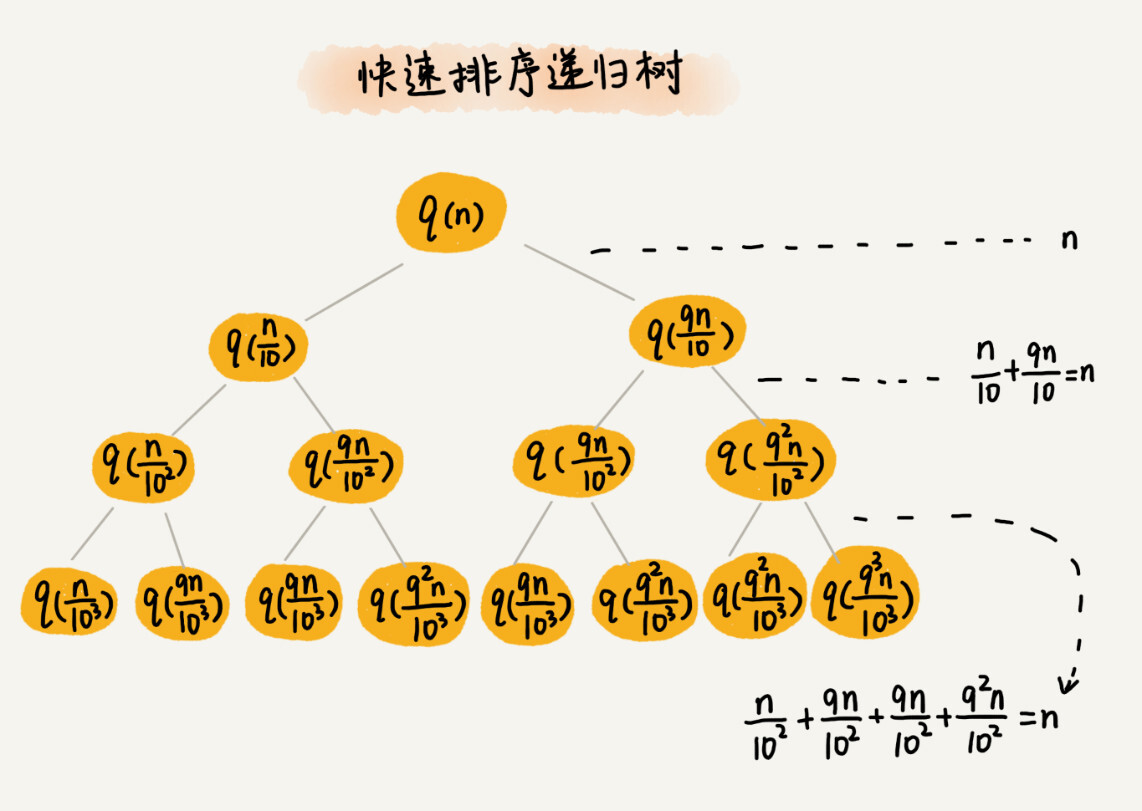
快速排序的过程中,每次分区都要遍历待分区区间的所有数据,所以,每一层分区操作所遍历的数据的个数之和就是n。我们只要求出递归树的高度h,这个快排过程遍历的数据个数就是h*n。也就是说,时间复杂度就是O(h*n)。
我们知道,快速排序结束的条件就是待排序的小区间,大小为1,也就是说叶子节点里的数据规模是1.从根节点n到叶子节点1,递归树中最短的一个路径每次都乘以1/10,最长的一个路径每次都乘以9/10,通过计算,我们可以得到路径:
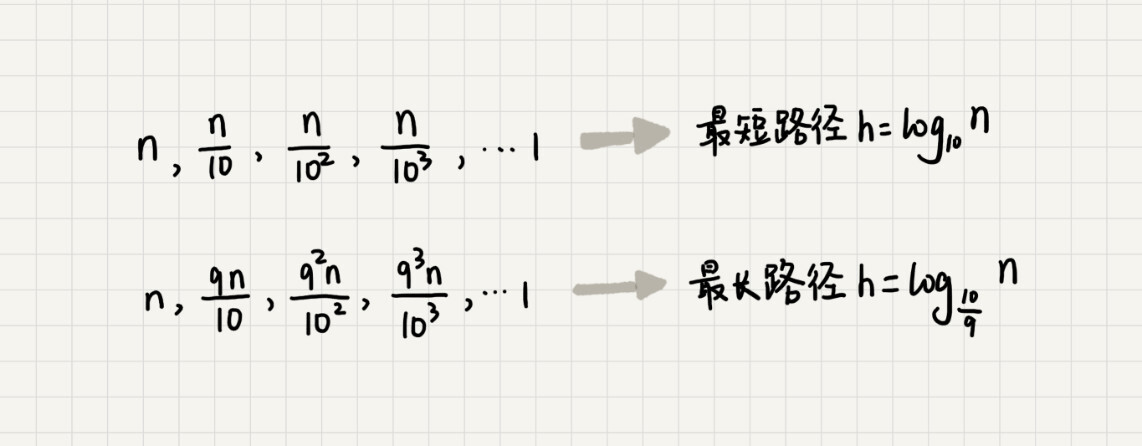
所以,遍历数据的个数总和就介于nlog10n,和nlog10/9n。根据复杂度的大O表示法,对数复杂度的底数不管是多少,我们都是写成logn,所以快速排序的平均时间复杂度就是O(nlogn)。
2.分析斐波拉契数列的时间复杂度
int f(int n) {
if (n == 1) return 1;
if (n == 2) return 2;
return f(n-1) + f(n-2);
}
斐波拉契的代码在上面,把它画成递归树的样子就是这样:
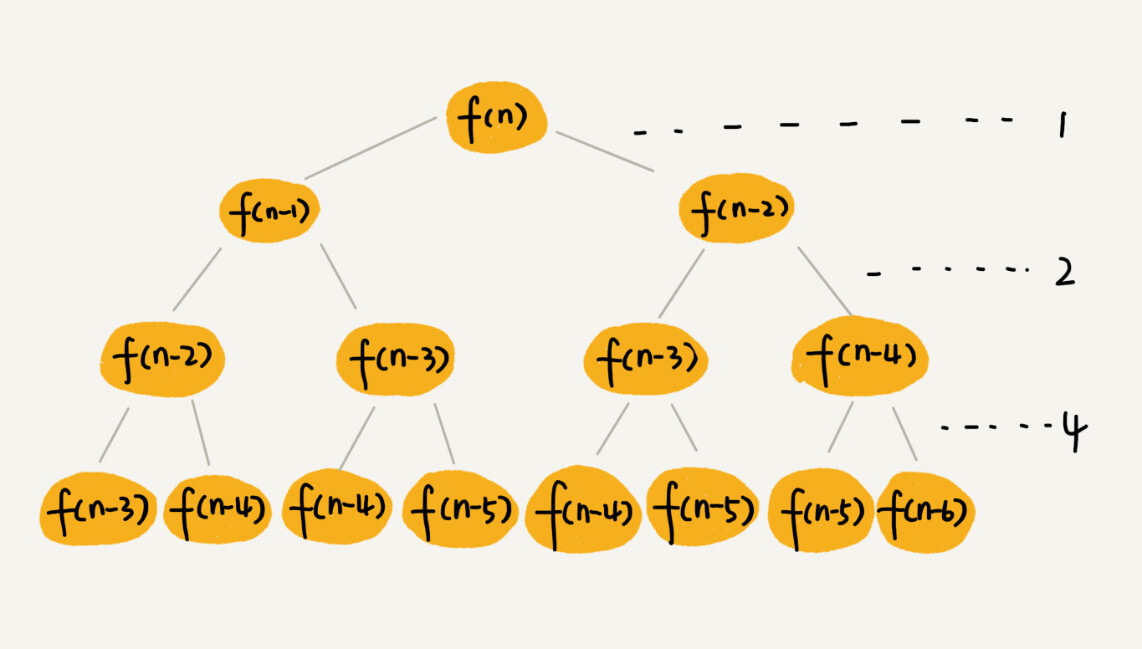
f(n)分解成f(n-1)和f(n-2),每次数据规模都是-1或者-2,叶子节点的数据规模是1或者2。所以,从根节点走到叶子节点,每条路径还是长短不一的。如果每次都是-1,那最长的路径大约就是n;如果每次都是-2,那最短路径大约就是n/2。
每次分解之后的合并操作只需要一次加法操作,时间复杂度是O(1),所以,从上往下,第一层的时间消耗是1,第二层就是2,第K层的时间消耗即使2^(k-1),那整个算法的总的时间消耗就是每一层时间消耗之和。
如果路径长度是n,那这个总和就是2^n -1。
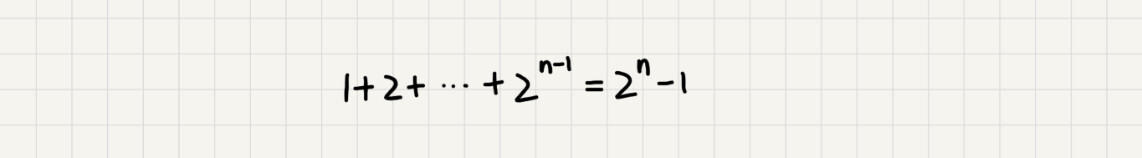
如果路径是n/2,那这个总和就是2^(n/2) -1 。
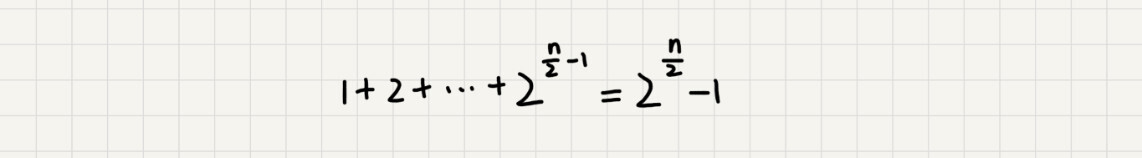
虽然不精确,但是我们也基本上知道了上面算法的时间复杂度是指数级的,非常高。
3.分析全排列的时间复杂度
我们在高中的时候都学过排列组合。“如何把n个数的所有排列都找出来”,这就是全排列的问题。
比如1,2,3,这三个数字有下面这几种不同的排列:
1, 2, 3
1, 3, 2
2, 1, 3
2, 3, 1
3, 1, 2
3, 2, 1
如何实现呢?如果我们确定了最后一位数据,那就变成了求解剩下n-1个数据的排列问题。而最后一位数据可以是N个数据中的任意一个,因此它的取值就有N种情况,所以n个数的排列问题,就可以分解成n个“n-1个数据的排列”的子问题。
写出递推公式如下:
假设数组中存储的是 1,2, 3...n。
f(1,2,...n) = {最后一位是 1, f(n-1)} + {最后一位是 2, f(n-1)} +...+{最后一位是 n, f(n-1)}。
把递推公式转化成代码如下:
void full_sort(int* array,int size,int used){
if(used == 1){
for(int i=0;i<size;++i){
cout << array[i] << " ";
}
cout << endl;
return;
}
for(int i=0;i<used;++i){
// 交换
int temp = array[i];
array[i] = array[used-1];
array[used-1] = temp;
full_sort(array,size,used-1);
temp = array[i];
array[i] = array[used-1];
array[used-1] = temp;
}
}现在我们使用递归树来分析一下这个算法的时间复杂度:
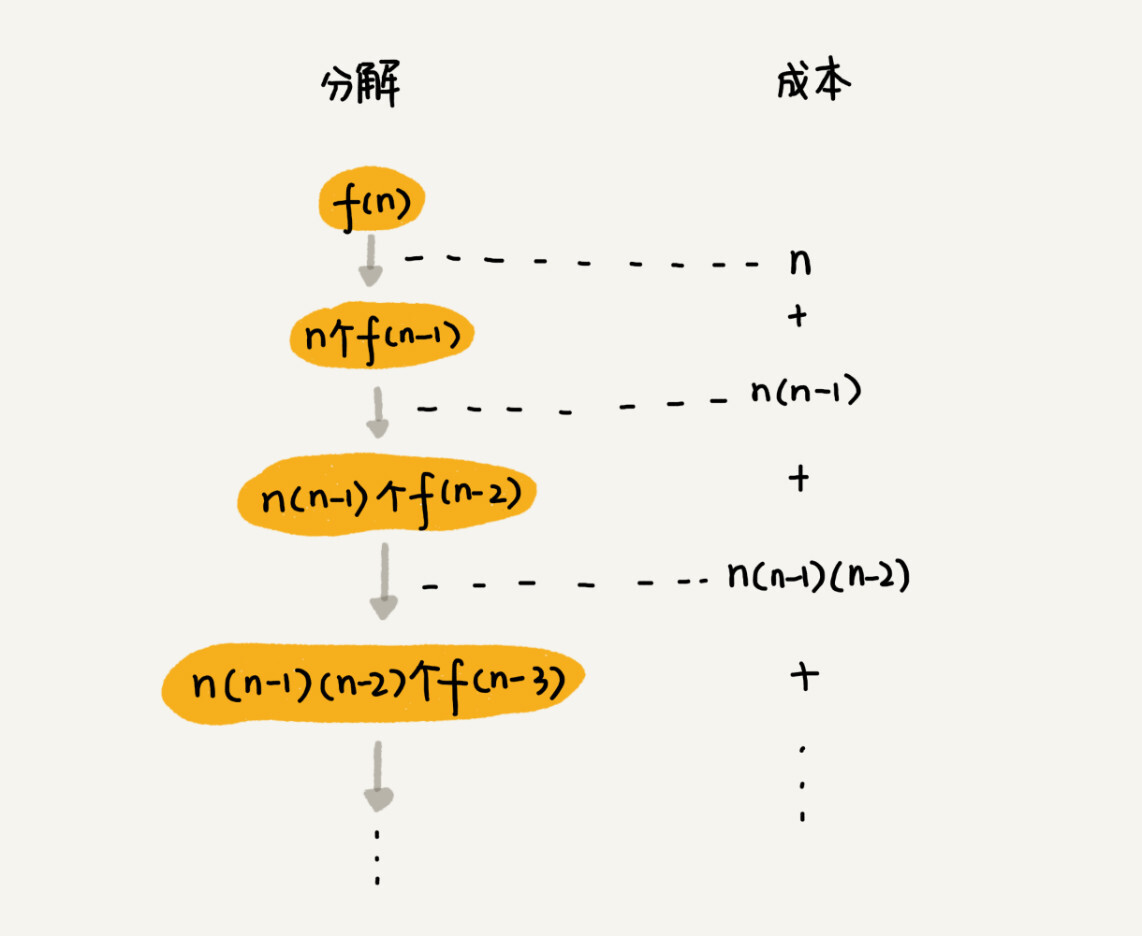
第一层分解有N次交换操作,第二层有n个节点,每个节点分解需要n-1次交换,所以第二层总的交换次数是n*(n-1)。第三层是n*(n-1)个节点,每个节点分解需要n-2次交换,所以第三层总的交换次数是n*(n-1)*(n-2)。
以此类推,第k层的交换次数就是n*(n-1)*(n-2)*...*(n-k+1)。最后一层的交换次数就是n*(n-1)*...*2*1。每一层的交换次数之和就是总的交换次数。
n + n*(n-1) + n*(n-1)*(n-2) +... + n*(n-1)*(n-2)*...*2*1
我们知道,最后一个数,等于n!,而前面的n-1个数都小于最后一个数,所以总和肯定小于n*n!。也就是说,全排列的递归算法的时间复杂度大于O(n!),所以全排列的时间复杂度非常高。