SVD奇异值分解可运用在降维算法PCA中进行特征分解,在机器学习等领域有广泛应用,所以很有必要将它搞清楚。
优秀文章:https://www.cnblogs.com/pinard/p/6251584.html
一、特征值与特征向量
其中,A是一个n×n的方阵,x为n维向量,是一个实数。那么,x为A的一个特征向量,
为A的一个特征值。这样我们可以将矩阵A特征分解,如果我们求出了A的k个特征值λ1≤λ2≤...≤λk,和对应的n个特征向量x1->x2->...->xk。如果这些特征向量线性无关,那么矩阵A就可以用下面式子进行特征分解。
其中,W为{x1,x2,...,xk},即A的k个特征向量组成的n×k的矩阵,为以k个特征值做主对角线的对角矩阵。一般的,我们会把这k个特征向量标准化(二范数为1),那么就会有
,则会有下式。
列向量的线性组合结果是权重向量的延伸。特征值与特征矩阵的计算如下。
要进行特征分解,矩阵A必须为方阵,若A不是方阵时,我们使用SVD。
二、SVD的定义
其中,A是一个M*N的矩阵,U是一个M×M的矩阵,同上是一个M*N对角矩阵,主对角线由奇异值组成的奇异矩阵,V同上是一个N*N的酉矩阵,有
,且有
,分别为左右奇异矩阵。
三、SVD的应用
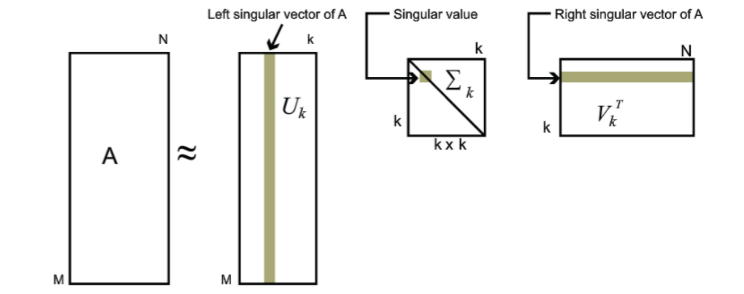
如图所示,奇异值与特征值类似,在奇异矩阵中,奇异值也是从大到小排列的,我们可以使用最大的k个奇异值和左右2k个奇异向量来表示原矩阵A。