李宏毅ML lecture-13 unsupervised Learning Principle Component Analysis
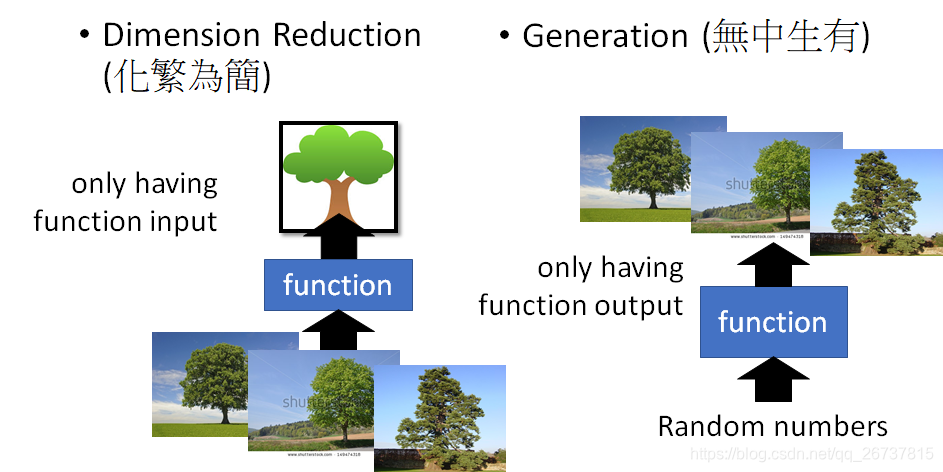
这个课呢讲解无监督学习中的两大类,数据降维和生成模型.
数据降维先专注于线性降维.
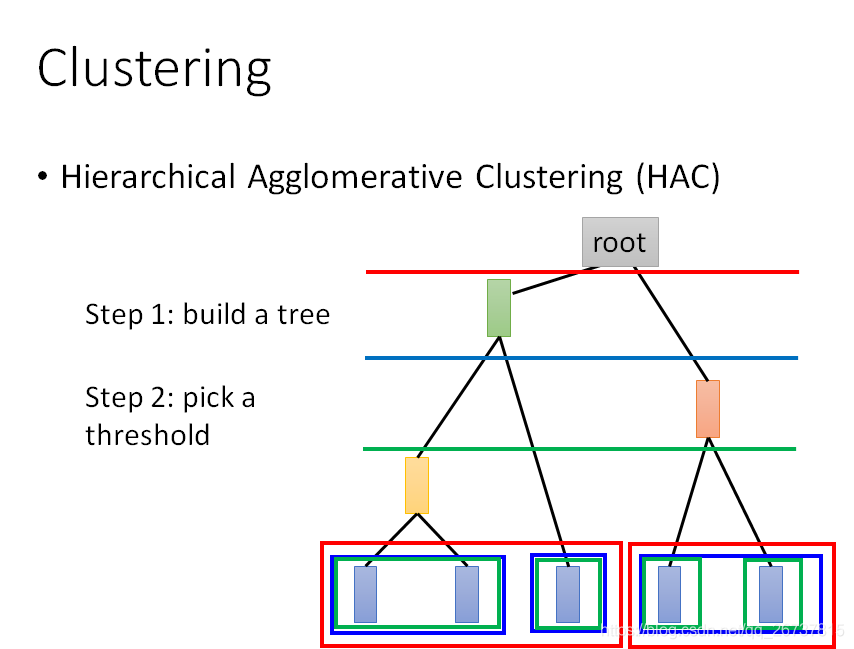
聚类(Clustering)
K-means

HAC
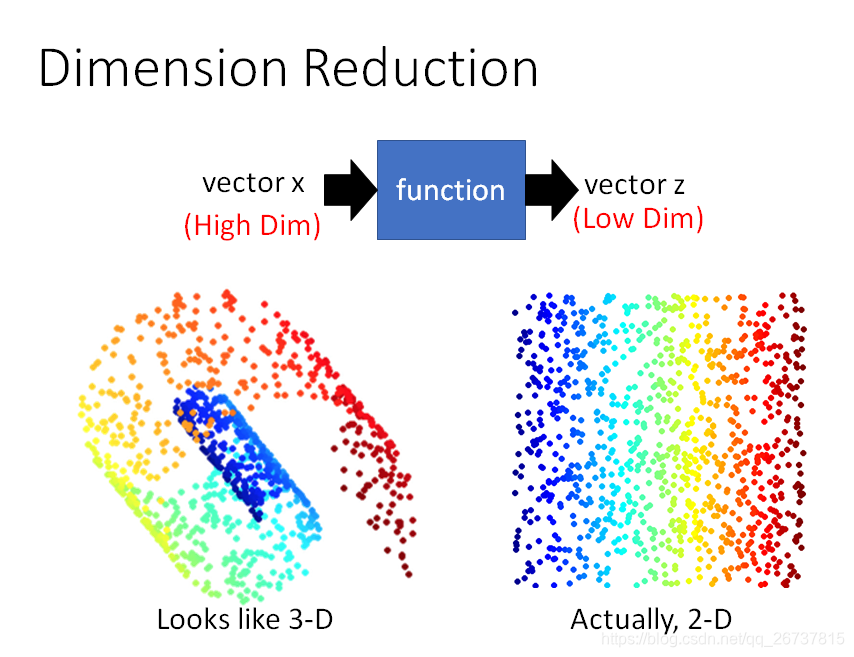
数据降维(Dimension Reduction)
数据降维直观上看这张图就能知道,高维空间中的特点可以在低维空间表示.
再举例来说,一张数字图片大小为
,但是表示数字的信息的像素点是很少的.
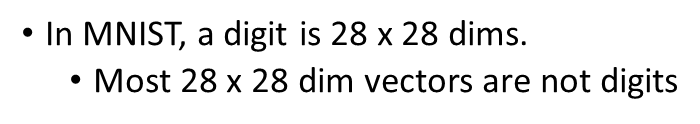

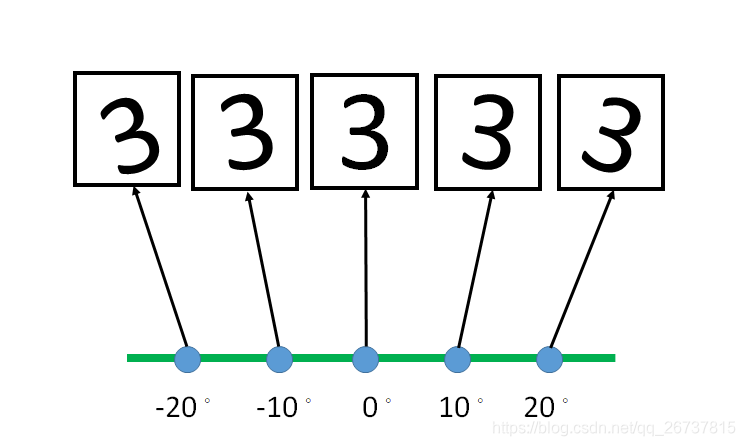
一张3的图片,经过旋转之后,还是3,但是计算机得到的是另外4张图片.
而这4张图片可以用一个仿射变换矩阵得到,这样数据得到了压缩.
如何做降维呢?
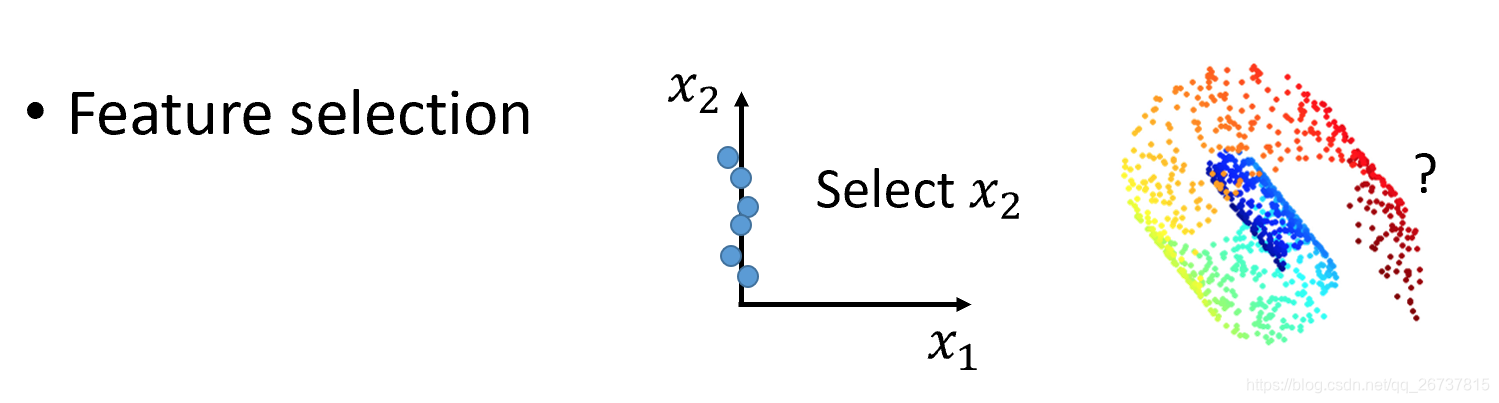
第一种方法叫Feature selection:把没有用的维度去掉
第2种就是PCA
PCA(Principal Component Analysis)
PCA就是一个线性函数,输入一个高维向量输出一个低维向量.


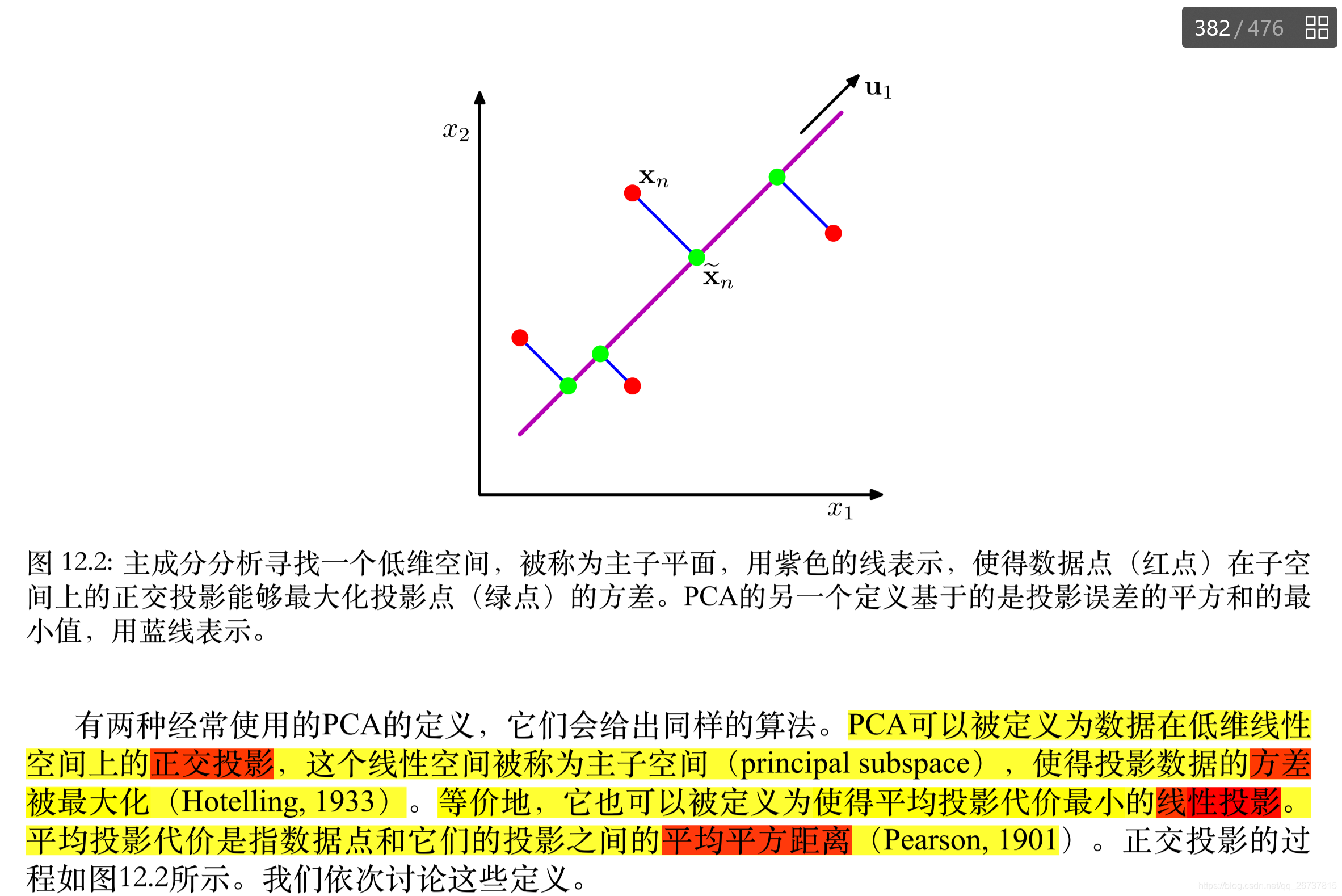
这里引用了Bishop 对于PCA的定义.
再补充一个大佬的博客
PCA的做法就蕴含在定义中.
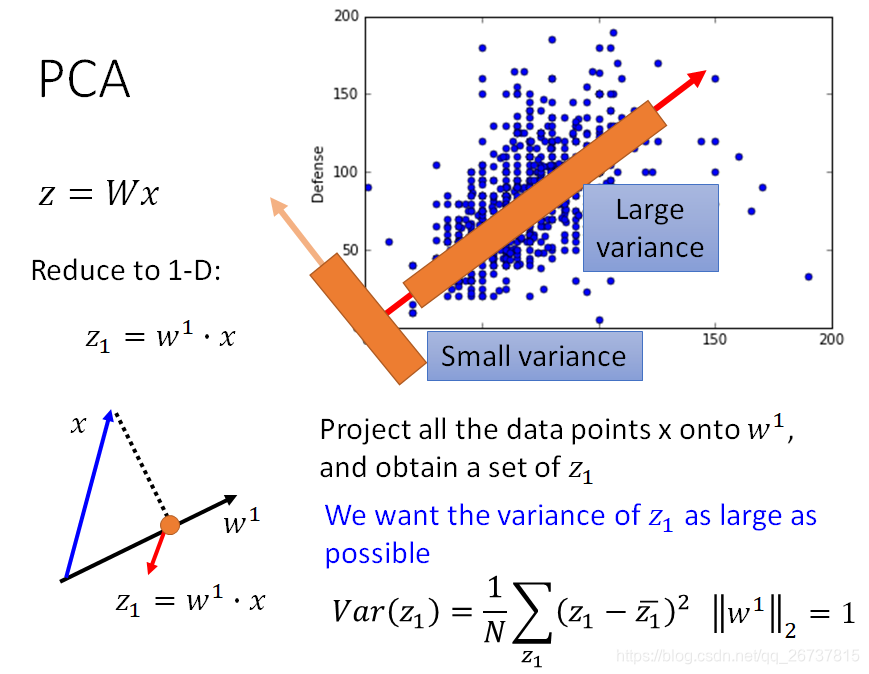
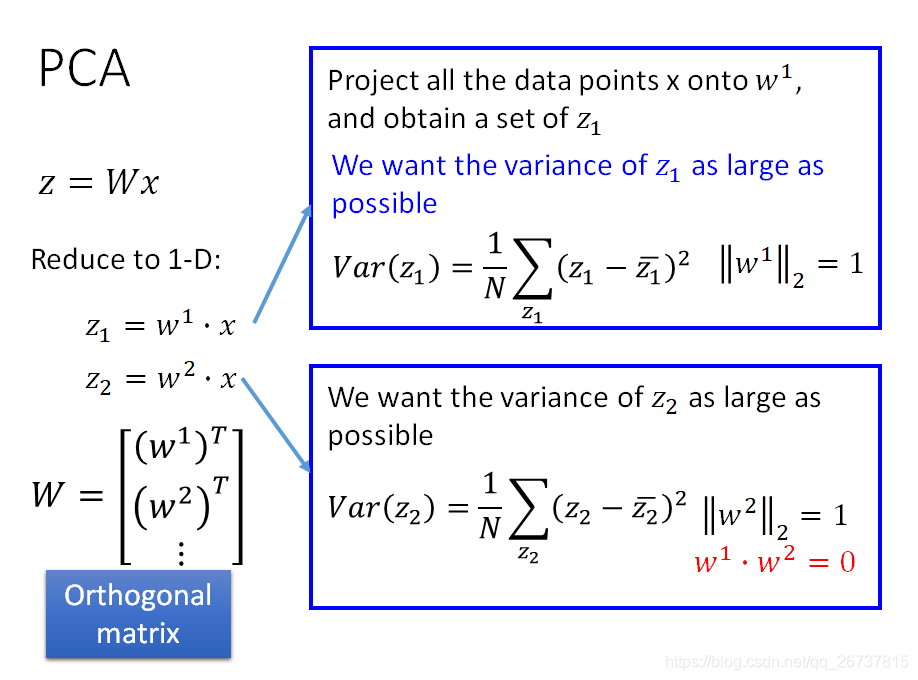
先找
,使得
的方差最大:
再找
,使得
的方差最大,同时保证
与先找到的
垂直,以此类推,找到所有的
.所以最终的
是一个正交矩阵(Orthogonal matrix):
在大佬的博客中,其实就说的非常清楚了:

PCA降维到k维,这个k就是一个超参数,是需要自己决定的.下图中的M既是k.


下面的推导需要注意:
表示内积
表示矩阵乘积
下面推导后的结果就是:
让投影后方差最大等价于让
最大.
是数据的协方差矩阵
同时规定
作为限定条件
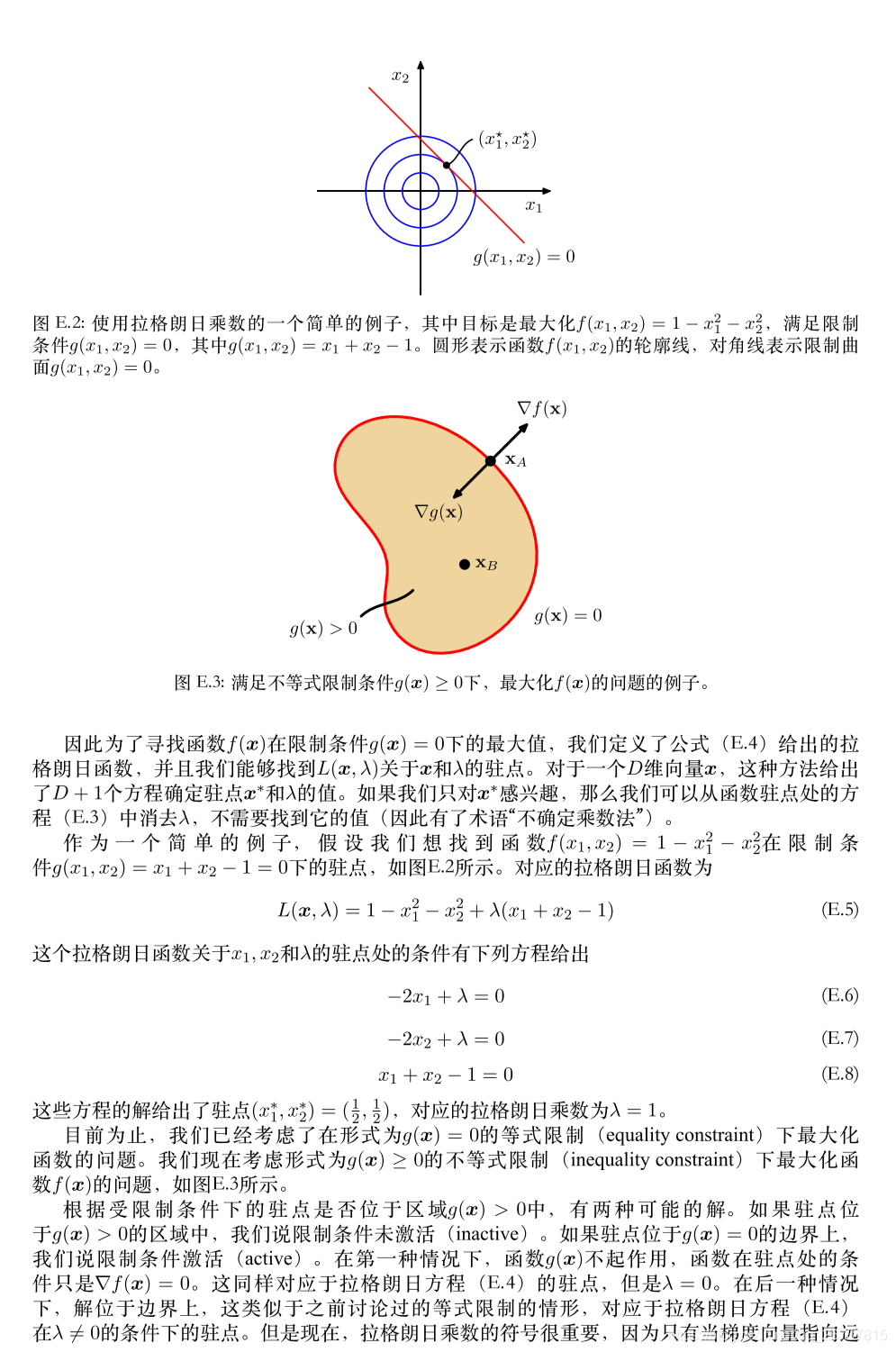
这个条件就可以用拉格朗日乘数法带入,找到
如果对推导有困难,可以先看后面的PRML中的特征向量和拉格朗日乘数法.

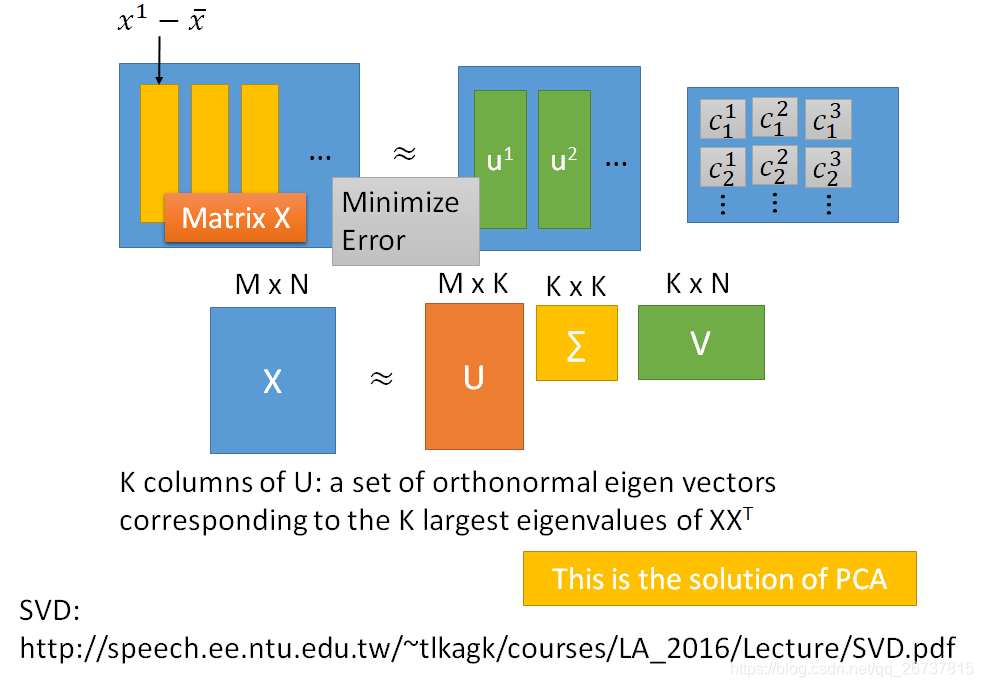
基于特征值分解协方差矩阵实现PCA算法
因为 是数据的协方差矩阵,所有具有一些性质:
- 是对称的(Symmetric)
- 是半正定矩阵(Positive-semidefinite): 设 为实对称矩阵,若对于每个非零实向量 ,都有 ,则称A为半正定矩阵,称 为半正定二次型。
- 的特征值(eigenvalues)都是非负的
- eigenvector是特征向量
通过推导得到结论:
计算数据矩阵的协方差矩阵,然后得到协方差矩阵的特征值特征向量,选择特征值最大(即方差最大)的k个特征所对应的特征向量组成的矩阵。
下图为k=1:

下图为k=2:
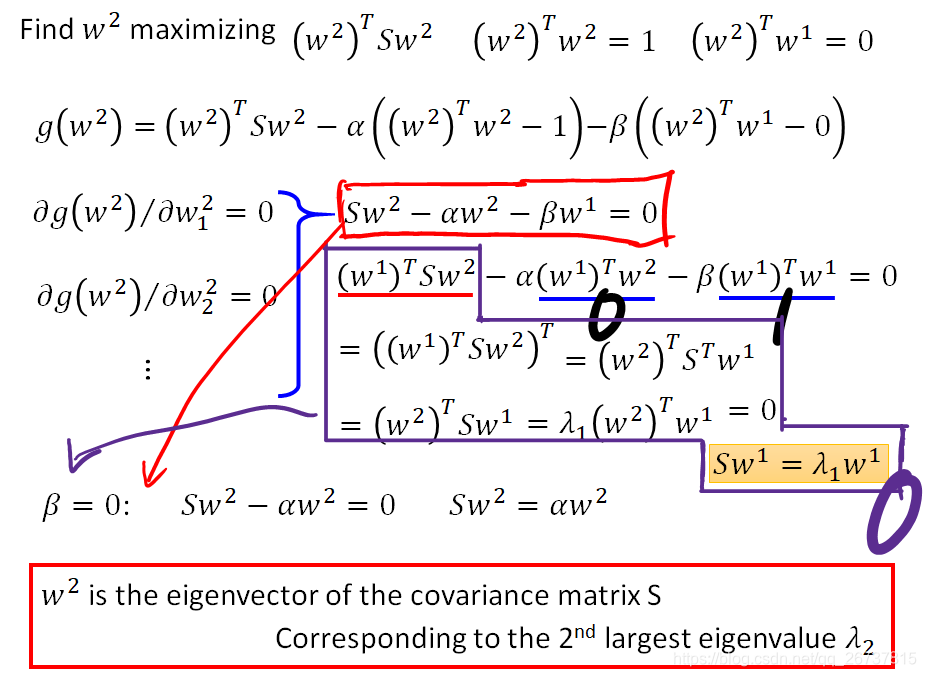
求偏导得到红色框公式:
左乘
推导得
红色框公式带入
得黄色框公式
所以
是特征向量
因为最大的特征值对应的特征向量是
所以为了使
最大
就是第二大特征值对应的特征向量

对角矩阵(diagonal matrix)

特征向量



拉格朗日乘数法


基于SVD分解协方差矩阵实现PCA算法
假设在MNIST上的数字都是由不同的笔画组成,每一个数字可以看作是笔画的线性组合.
我们提取的笔画数远远小于像素数,就完成了数据降维.
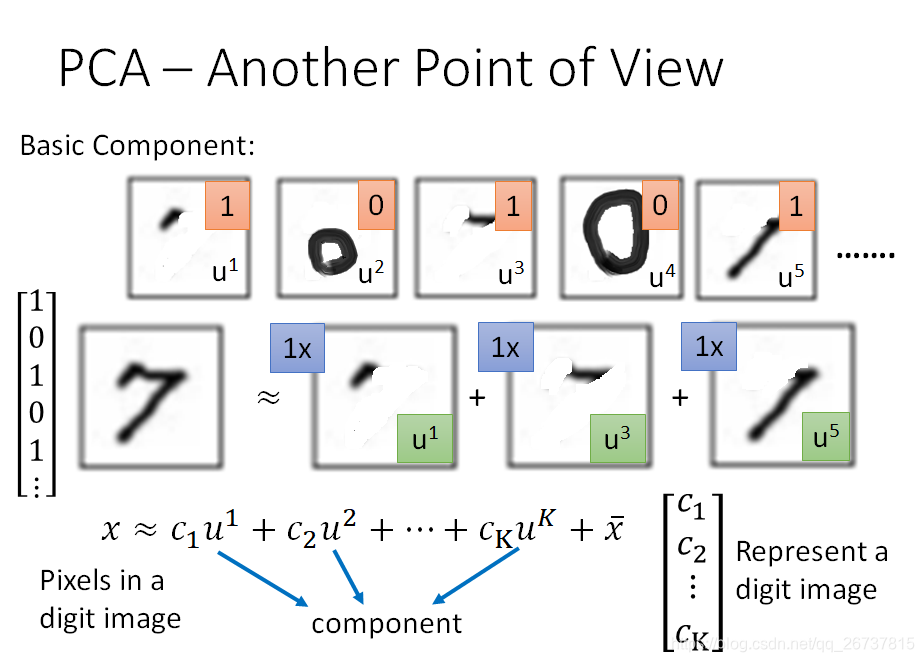
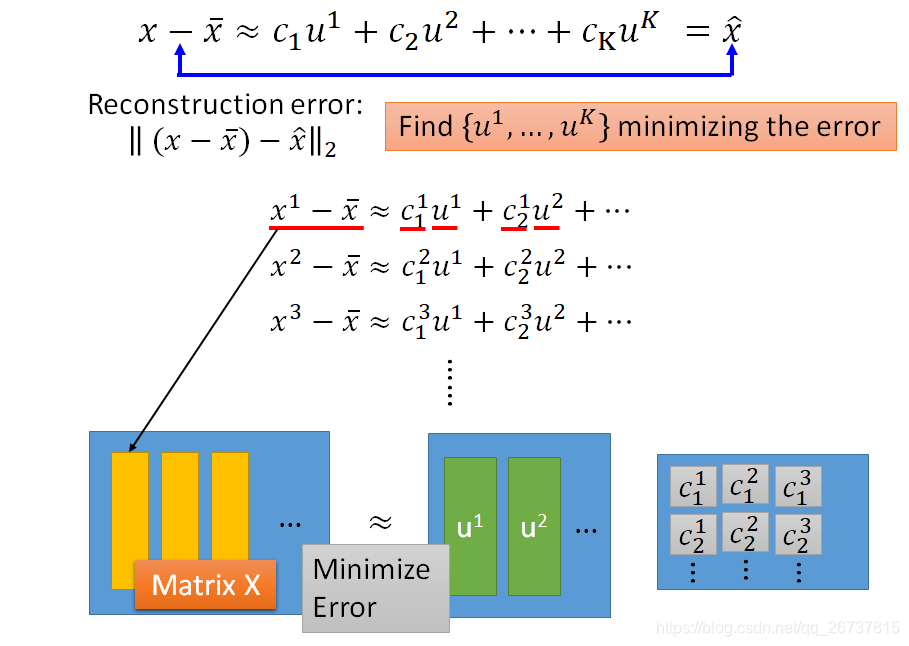
在定义中一个digit由component线性组成,再加一个digit的平均
digit:
digits的平均:
component线性组成:
和
是已知的,目标就是最小化
与
之间的重构误差(reconstruction error)


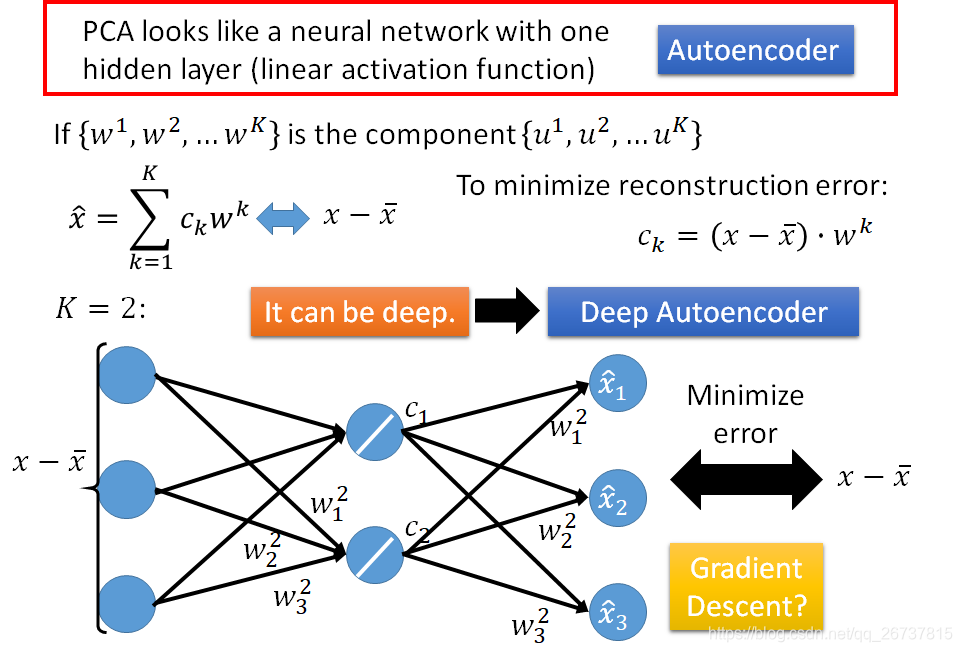
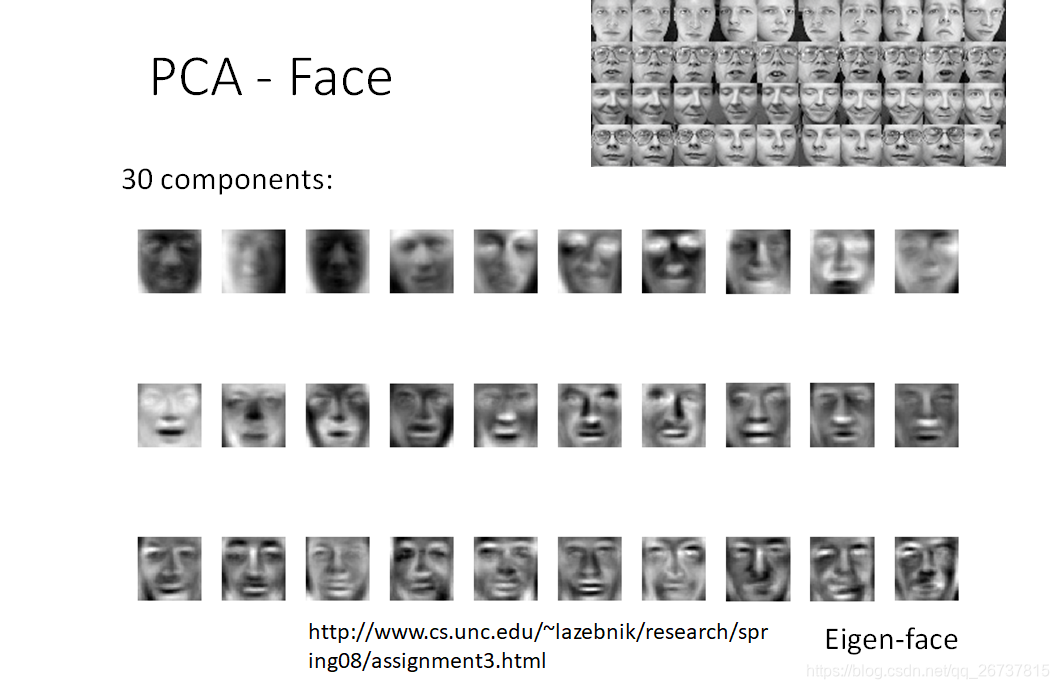
PCA通过神经网络实现
注意这时候
不能保证是正交矩阵
PCA在数据可视化的例子

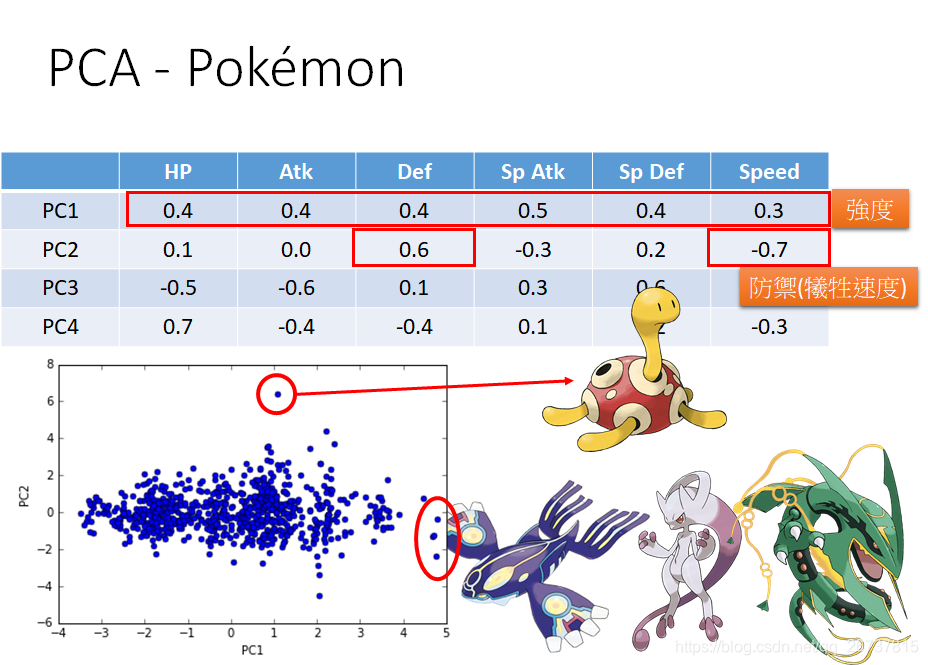
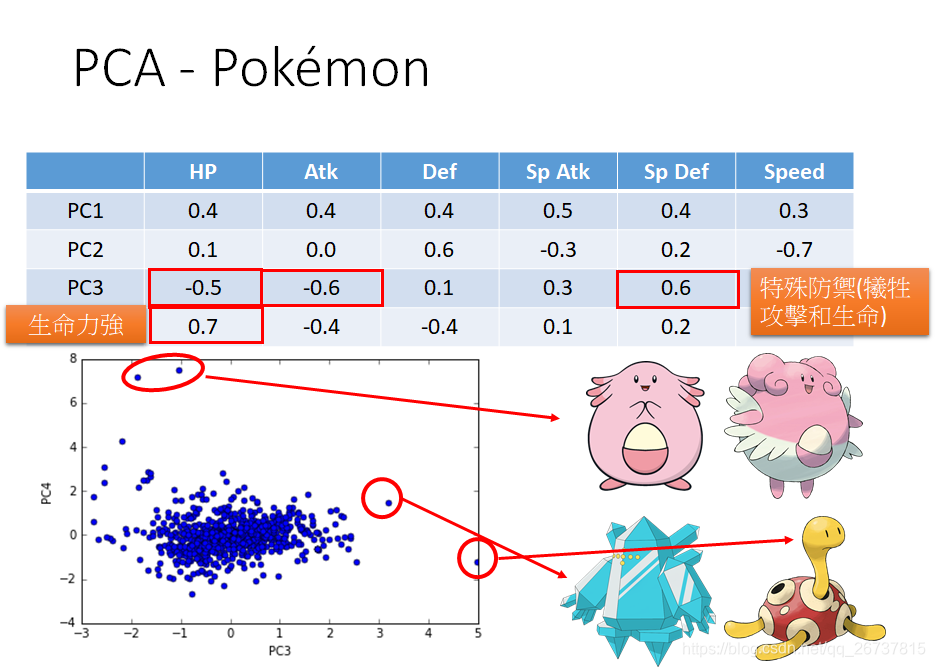
- http://140.112.21.35:2880/~tlkagk/pokemon/pca.html
- The code is modified from http://jkunst.com/r/pokemon-visualize-em-all/

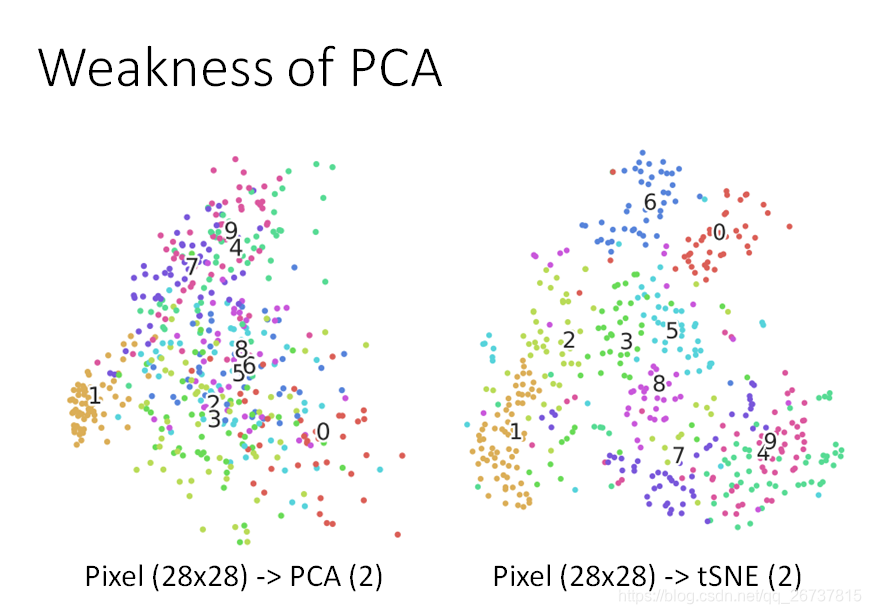
Weakness of PCA
- 无监督的
- 线性的

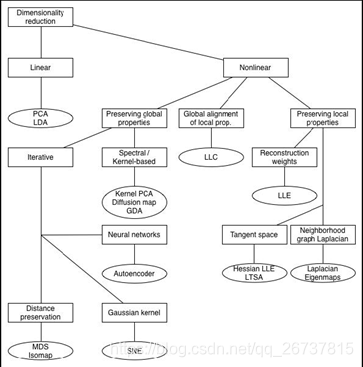
PCA的扩展
- http://4.bp.blogspot.com/_sHcZHRnxlLE/S9EpFXYjfvI/AAAAAAAABZ0/_oEQiaR3WVM/s640/dimensionality+reduction.jpg
- https://lvdmaaten.github.io/publications/papers/TR_Dimensionality_Reduction_Review_2009.pdf
矩阵分解(Matrix Factorization)
https://datajobs.com/data-science-repo/Recommender-Systems-[Netflix].pdf
