开篇寄语

一直想总结下机器学习相关的知识，先从最简单的LR开始吧，温故而知新吧。自己的写作功底比较弱，所以也借鉴了几位前辈的博客

1、Sigmoid 与 Logistic Regression

sigmoid函数是lr的核心，它将普通的现行回归值域映射到了[0,1]
$g(z)=\dfrac{1}{1+e^{-z}}$
回顾一下线性回归， $h_{\theta}(x)=\theta^{T} X$ ，令 $z=h_{\theta}(x)$ ，代入公式可得到
$g(x)=\dfrac{1}{1+e^{-\theta^{T}X}}$
实际上，逻辑回归是非线性回归的一种，只不过能用于二分类问题，所以很特殊，也很经典。
（PS：不知道还有没有其它可用于分类的非线性回归，或者只是sigmoid简单的变形）

2、概率分布

为什么LR能用于二分类问题呢，我们来算一下，首先是Y为0或者1的条件概率分布
$P(Y=1|X) = \frac{1}{1+e^{-wx}} = \frac{e^{wx}}{1+e^{wx}}$
$P(Y=0|X) = 1- P(Y=1|X) = \frac{1}{1+e^{wx}}$
发生事件的几率定义为发生与不发生的比值
$odds = \frac{p}{1-p}$
取其对数概率
$logit(p)=log\frac{p}{1−p}$
那么Y=1的几率就是
$log \frac{P(Y=1|x)}{1−P(Y=1|x)}=log \frac{P(Y=1|x)}{P(Y=0|x)}=w.x$
即，当 w.x的值越大，P(Y=1|x) 越接近1；w.x越小(f负无穷大),P(Y=1|x) 越接近0，
其实这个从sigmoid图像也可以看得出来，不过另外一位先辈是这样写的，先暂且这么理解

3、参数求解

我们用最大化似然函数来估计参数，首先构建最大似然函数
$L(\theta) = \prod P(y_i=1|x_i)^{y_i}(1-P(y_i=1|x_i))^{1-y_i}$
对最大似然函数取对数并化简

$LL(\theta) = log(L(\theta)) = log(\prod P(y_i=1|x_i)^{y_i}(1-P(y_i=1|x_i))^{1-y_i})$

$= \sum_{i=1}^{n}y_i log P(y_i=1|x_i) + (1-y_i)log(1-P(y_i=1|x_i))$

$= \sum_{i=1}^{n}y_i log \frac{P(y_i=1|x_i)}{1-P(y_i=1|x_i)} + \sum_{i=1}^{n}log(1-P(y_i=1|x_i))$

$= \sum_{i=1}^{n}y_i(w.x) + \sum_{i=1}^{n}logP(y_i=0|x_i)$

$= \sum_{i=1}^{n}y_i(w.x) - \sum_{i=1}^{n}log(1+e^{w.x})$

扫描二维码关注公众号，回复： 5298025 查看本文章

$= \sum_{i=1}^{n}y_i(\theta^T.x_i) - \sum_{i=1}^{n}log(1+e^{\theta^T.x_i})$

我们无法从这个公式求一个全局最优解（目前），但是我们可以从各个维度去逼近最优解，所以对上面的公式求偏导即可得：
$\frac{\partial LL(\theta)}{\partial \theta} = \sum_{i=1}^{n}y_ix_i - \sum_{i=1}^{n} \frac{e^{\theta^T.x_i}}{1+e^{\theta^T.x_i}}.x_i = \sum_{i=1}^{n}(y_i - P(y_i=1|x_i))x_i$

4、梯度下降

上面我们对公式求偏导，可以在各个维度上逼近最优解。优化方法有很多种，梯度下降是最早和最经典的一种，其求解公式为：
$\theta^{new} = \theta^{old}-\alpha\frac{\partial LL(\theta)}{\partial \theta} = \theta^{old} - \alpha\sum_{i=1}^{n}(y_i - P(y_i=1|x_i))x_i$
其它的优化方法，再开一个帖子专门讲

5、正则化

正常LR的参数估计到上一步梯度下降就已经结束了，但是，可避免的会出现过拟合的现象，所以引入了正则化的方法，一定程度上可以缓解这种情况
目前有两个正则化范数可以用，即L1范数与L2范数
L1范数：也称叫“稀疏规则算子”（Lasso Regularization），泛化能力比较差，：引入是为了实现特征自动选择，它会将没有信息的特征对应的权重置为0
L2范数：在回归里面中又称岭回归”（Ridge Regression），与 L1 范数不同的是L2是使得特征对应的权重尽量的小，接近于0，越小的参数说明模型越简单，越简单的模型则越不容易产生过拟合现象，为什么呢？
首先，我们看损失函数
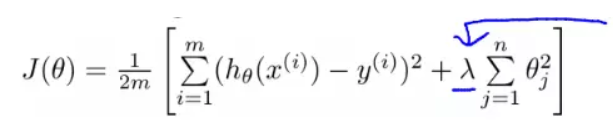
在这里插入图片描述
想让损失函数趋近于0，则需让函数的两部分无限重合，如下图

L1倾向于使某些特征对应的参数变为0，因此能产生稀疏解。而 L2 使 w 接近0

引用
[1]: https://blog.csdn.net/buracag_mc/article/details/77620686
[2]: https://www.jianshu.com/p/a47c46153326
[3]: https://blog.csdn.net/yumei7865/article/details/75194772

LR（逻辑回归）