上一讲学习了Linear Regression。首先,我们从问题出发,想要找到一条直线拟合实际数据值;然后,我们利用最小二乘法,用解析形式推导了权重w的解;接着,用图形的形式得到Eout-Ein≈2(N+1)/N,证明了linear regression是可以进行机器学习的;最后,我们证明linear regressin这种方法可以用在binary classification上,虽然上界变宽松了,但是仍然能得到不错的学习方法。

这一讲继续学习一种叫Logistic Regression的算法,看似一种回归算法,实则是一种分类算法。主要从以下的四个方面对于算法进行一个学习。

首先在前面的二分类问题中,我们需要算法给出一个非此即彼的答案,也就是形式化的给出最后是+1还是-1,所以使用如下的公式输入x便可得到想要的答案

但是在实际中算法很难根据给定的数据给出确定的答案,比如在预测心脏病复发的例子中,医生不能准确的告诉病人是否一定会发生复发,它只能给出一个概率值,表示有多大的可能会复发。这种实际上的情况我们称分类模型为soft binary classification:它给出的的是一个结果是+1时的位于[0,1]之间的概率值,这个值越接近1,表示发生的可能性越大,越接近0,表示发生的可能性越小

因此我们将上面的f称为这里的target function

在理想(无噪声)的数据中,给定输入x输出y应该就是为+1(或是-1)的具体的概率值,如左下图所示,但是实际中我们得到的数据是由下图所示的形式,并没有一个具体的值,只是某种分类的结果。在这种形式数据的情况下,需要找到一个好的假设h来很好的接近我们的target function

下面来看一下如何得到这个假设。我们还拿前面心脏病的例子来看,假设病人的数据有如下的一系列的指标
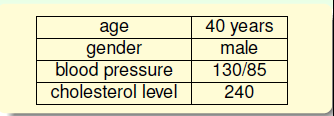
按照前面学习的模型,用xi来表示这些特征,同样为了表示方便加上了x0,接着算一个加权的和值作为最后输出的分数。但是按照算法的思想,我们需要将其转换为0到1之间的一个数,故要有一个logistic function:θ(S),来完成这一功能,那么如果有这么个合适的函数,我们的假设就如下所示

在实际中最常用的θ(S)为如下所示的sigmoid function,这个函数是平滑、单调的S形函数,它的图像如下所示,具体的可参见之前写过的一篇介绍性的博客Logistic Regression

通过取值可证明它可以满足我们转换的要求,带入上面的假设,最后用的logistic function是如下的h(x)来逼近目标函数f(x) = P(y|x)

在得到了logistic function后,我们和之前学习的几种模型做一个对比。相同处在于都使用了有关输入的加权和的形式的输入,但是在线性分类中,我们使用的误差衡量是0/1error,最后通过sign(x)函数给出分类的结果;在线性回归中,使用平方误差,最后给出的就是加权的结果;那么在logistic 回归中,我们的h如上所示,在这里使用什么样的误差衡量来得到我们想要的Ein呢?

为了表述方便表述,做一下表达式的转换,将前面f(x)的形式变成有关于条件概率的样子,具体的形式如下所示

在此之前,先介绍一下“似然性”。当目标函数为f(x) = P(+1|x),如果我们找到了h很接近target function。也就是说,在所有的H集合中找到一个h与target function最接近,能产生同样的数据集D,包含y输出label,则称这个h是最大似然likelihood。
那么在给定的实际的数据集中,如果将输入连乘起来,会有下面的表达;再将似然函数h带入后变成了右面的样子

在经过上面的转换后,如果我们的h可以很好的接近f,那么似然函数h就可以很大可能的代替f(我们认为f可以很大概率的得到数据中的结果)

那么最后想要的g就是那个可以得到最大似然函数值的h。

因为h的对称性,有1-h(x) = h(-x)

所以可以将likelihood(h)转换成下面的形式,正比于输入的乘积。这里的P(xi)用灰色表示,是因为它对所有的h都是一样的,所以可以忽略。

在知道了假设的函数表示和似然函数后,我们要用什么样的误差衡量标准呢?根据前面的推导,我们的目标如下,公式中未知的是h

将前面h的表达式带入后,变成了关于w的表达式
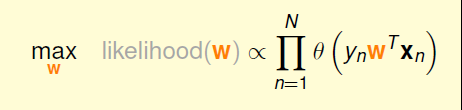
这里式子是连乘的形式,为了方便计算可取对数后,将其变成连加的形式
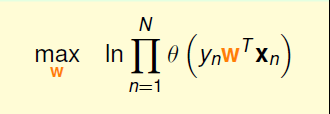
再取它的对偶问题

然后将θ(s)带入后,我们最终的目标就如下所示,将后面的作为要求的Ein。这里使用的误差衡量就是cross-entropy error(交叉熵误差)。

经过上面的分析,得到了我们想要的为最小化Ein
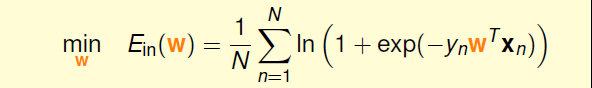
仔细论证可以发现,这里的Ein的表达式仍然连续、可微、二次可微的凸曲线(开口向上),根据之前线性回归的学习,我们仍然可以使用梯度下降法,只要计算的梯度为零时的w,即为最优解

经过一些代换来完成梯度的计算,最后可得到最下面的表达式,具体的计算过程不算难,这里也不打算给出

得到了梯度的表示后,目标就是求其值为零的点
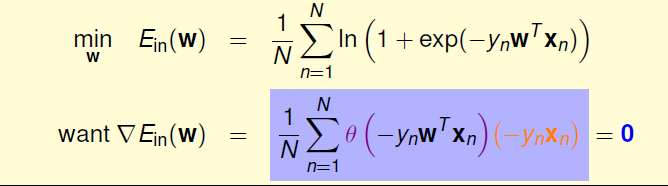
这里可以将其看成一种加权和的形式,要是表达式为零,则要求所有的θ的表达式为零。而这种情况成立只有在橙色部分远大于零,也就是让表达式中的所有输入都同号才成立,即数据集线性可分时才满足。
但是,保证所有的权重为0是不一定满足的,总有不等于0的时候,一种常见的情况是非线性可分,只能通过使加权和为零,来求解w。这时就不能使用前面求解析解的方式求解,只能用迭代方法求解。

在线性回归中,我们可以说最后的解是“一步就求出来的”,但是在这里不能使用。所以只能从其他方法中找,而PLA求解的思路就可以。在PLA中我们知道求解过程是迭代进行的,在每一步不断修正错误,直到最后停止得到想要的g

在logistic regression中,采用一种等价的形式。类似的这种方法,我们称之为iterative optimization approach。

上一讲提出了一个iterative optimization 的方法,每一次迭代优化都需要更新W,当更新停止,便得到了想要的g

类似于前面讲的梯度下降,将Ein最小化的过程看成了将小球从一个坡滚下的过程,在下降的过程中主要受两个因素的控制:
- V:控制下降的单位方向
- η:控制下降的步长
一种贪婪的方法就是设v的大小为1,步长大于0,通过迭代求出最小的Ein

由于图像是曲线的,难以直接用直线的方法求解,但是学过微分的都知道“以直代曲”,当我们下降的步长很小,即曲线很短时,就可以将其看成是直线来处理。当η很小时,根据泰勒展开,可以将Ein的表达式转换成如下的样子

在这个表达式中Ein(Wt)和η不影响求解的过程,所以关注点在后面的那个部分,故前面的那两个为灰色。迭代的目的是让Ein越来越小,即让Ein(wt+ηv)<Ein(wt)。η是标量,因为如果两个向量方向相反的话,那么他们的内积最小(为负),也就是说如果v方向与梯度部分反向的话,那么就能保证每次迭代Ein(wt+ηv)<Ein(wt)都成立。则,我们令下降方向v为下面的样子,所以更新的公式也就发生了改变

那么其中的常量η对于在整个更新的过程中起到怎样的作用呢?通过下面三幅图来看一下,当我们的η很小时,下降的步长就很小,就像人迈小碎步下山一样,会到达谷底,但是速度太慢;如果选择太大的话,就会出现激荡,不易到达谷底;最好的方法就是当坡度较大的时候下降的速度快一些,当坡度较小时,下降的慢一些,故要经过实验选择一个合适的η

当η正比于 梯度时,将其变换一下成下面的形式,使用这个公式进行更新

在学习了前面的所有知识后,来总结下Logistic Regression的主要步骤:
• 初始化W0
• 计算梯度:主要的计算花销部分
• 迭代更新
• 当到达梯度为零的点或是迭代的最大次数后,算法结束

最后总结一下这一讲的内容:这一将主要介绍了Logistic 回归算法,首先从问题出发,选择目标函数和假设h,然后定义了误差衡量;接着计算了下降的梯度;最后计算到达梯度为零的点,得到相应的W矩阵,算法完成。
