接着上一讲学到的有关成长函数和breaking point的内容,最后留下一个猜测:2D perceptron的成长函数是不是多项式级别的呢?这一讲继续学习泛化的理论知识,进而回答这个问题。

上面我们对于不同的情况进行分析,给出了它们的mH(N)(给出了划分的最大的dichotomy)和breaking point的值。

当我们的N比较小时,我们可以手动模拟出breaking point的K的大小,但是当N很大时,我们就需要一种理论支持,可以较为轻松的给出breaking point的值。当K=1时,所有成长函数的值都是1,所以我们从k=2开始讨论我们的问题。当N=1时,我们的mH(N)为2,是有限的;当N=2时,前面我们得到的mH(N)最大是3<2^2,也是有限的

接下来我们来看一下在k=2的前提下,N=3是个什么样的情况?在这之前明白一个单词shatter:如果在k=2时,N个点能划分成2^N种dichotomy时,我们就说是可以被shattered。那么我们来看有多少种dichotomy时是可以被shattered的。有一种时的情形如下,我们任取其中两个点,并不能shatter
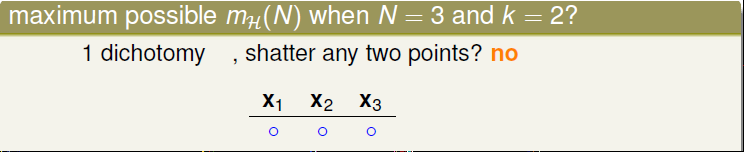
有2种dichotomy呢?第一行就是上面的的情形,显然不可以;第二行虽然出现了×,但是任取两点还是没有××,所以依然不能被shattered。
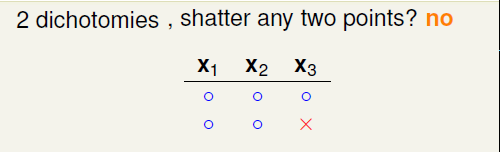
有3种dichotomy呢?同样分析可知,仍然不行,只有oo、xo、ox三种可能的情况。

那么4种呢?当我们的dichotomy是如下的情形时,我们选x2和x3两列我们就可以得到4种,这时是可以被shattered的。

当仍是4种,但是是这样的话,不管我们取哪两列,我们都得不到xx,所以是NO。

我们再接着往下看,当是5种dichotomy时,我们取x1和x3,是可以被shattered的。

我们就可以说在k=2,N=3的情况下,mH(N)的最大值为4。综上我们可以得到以下的结论

在这个过程中我们发现,当N大于K时,breaking point的值限制了成长函数值mH(N)的增长,即影响mH(N)的因素主要有两个:(1)数据集的大小N;(2)breaking point 的值。如果N和K是确定的,那么成长函数值的上界就是多项式级别poly(N)的。所以根据这些东西,就可以回答之前的问题,即我们可以用mH(N)的值代替M,从而使我们的学习是可行的,所以接下来我们要做的就是在数学上证明mH(N)上界是poly(N)。

为了我们的证明,引入一个新东西:bounding function B(N,K),他表示在breaking point确定为K时,我们的mH(N)的上界,即B(N,K)<=>MAX(Mh(N))<=>dichotomy的最大划分数。bounding function的引入使我们只需要关注mH(N)的上界值,不必考虑是哪一种情况,从而简化了问题的复杂度。
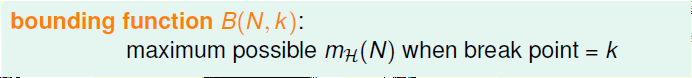
因此我们需要做的就是证明下式是成立的

目前我们已经知道的数据是这样的,后面要做的就是不断地完善这个表格。
当K=1时,不管我们的N取什么值,B(N,K)=1恒成立;
当N<K 时,根据之前breaking point的定义,B(N,K)=2^N
当N=K时,N是第一次出现不能被shatter的值,所以最多只能有个2^N-1dichotomies, 则B(N,K)=2^N-1。

接着我们填左下角的部分,首先我们来看一下B(4,3)它和前面的B(3,?)有什么关系呢?首先,把B(4,3)所有情况写下来,共有11组。也就是说再加一种dichotomy,任意三点都能被shattered,11是极限。

接着我们将11种情况进行分类,橘色的代表成对的,即只有x4是不同的,而紫色的是单独的。我们将橙色的部分记为2α,紫色的部分记为β,有2α+β=11,如果我们只看前三列那么就有α+β是x1、x2、x3的dichotomy,则B(4,3)在任意的三列都不会shatter,故有α+β<11即α+β<=B(3,3)。

另一方面,由于中x4是成对存在的,且是不能被任意三点shatter的,则能推导出α是不能被任意两点shatter的。这是因为,如果α是不能被任意两点shatter,而x4又是成对存在的,那么x1、x2、x3、x4组成的必然能被三个点shatter。这就违背了条件的设定。故有α<B(3,2)。

由上面的分析我们就可以得到

根据上式,我们就可以填出B(4,3)<=B(3,3)+B(3,2)=4+7=11。推广到一般,我们有公式

依据上面的一般化的公式,往后写就可以就表格写成如下的形式

根据B(N,K)的一般公式,给出它的递推公式
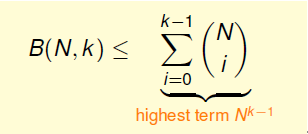
上述不等式的右边是最高阶为k-1的N多项式,也就是说成长函数值的上界B(N,K)的上界满足多项式分poly(N),这就解答了我们之前提出的猜测。得到B(N,K)的上界满足多项式分布poly(N)后,我们回过头来看之前的几种类型它们的成长函数值与break point的关系:

我们得到的结论是,对于2D perceptrons,break point为k=4, mH(N)的上界是N^k-1。推广一下,也就是说如果能找到一个模型的break point,且是有限大的,那么就能推断出其mH(N)有界。
在前面提到过,我们想要用成长函数值mH(N)来代替M,从而使得我们的学习是可行的。但是实际上,不是可以简单替代的,我们实际上得到的式子是最下面的那个。

那么上式是怎么得到的呢?我们可以简单的通过三个步骤看一下。首先我们知道Ein(h)是有限的,但是Eout是无限(不同的线可能只是稍微偏差一点,那得到的也是一条不一样的线)。
所以我们第一步要做的就是拿一个东西去替代它。假设我们有另外的N个点D’,对应的就是Ein’。如果我们将所有可能数据的Ein和Ein’都花在图上,我们可以得到一个大概这样的图,中点位置就是我们的Eout。假设我们有一个h使得Ein和Eout相差很大,那么就有很大概率使Ein’和Ein相差很远。即在发生不好的事情时,我们就可以将Eout替换为Ein’,不等式前的1/2表示发生的较大的概率,我们便可以得到下面的式子

替换之后,我们的Ein和Ein’都依赖于D和D’,那么我们将我们的假设集分为两部分,看在数据上的dichotomy是多少。根据前面的学习,我们union bound之后最多就有mH(2N)种。根据Hoeffding’不等式,在DataSet上每个h发生坏事的几率如图a所示那么多,那么使用union bound后我们认为所有可能发生的坏事如图b所示,我们要做的就是把不同h所发生的相同的坏事归到同一类中。在这样的思想下,我们用2N个点(N的D,N个D’),使用固定的h来探讨Ein和Ein’的差别。

接着我们有一个固定的h,我们想要比较两次抽样的差别,怎么做呢?假设我们的数据有2N个,我们可以抽N个出来,然后和剩下的N个比较,或者与全部的2N个作比较。经过这一步,我们的不等式就变成了下图所示的样子。

经过上面的步骤之后,我们就可以整理得到一个新的不等式VapnikChervonenkis(VC) bound如下
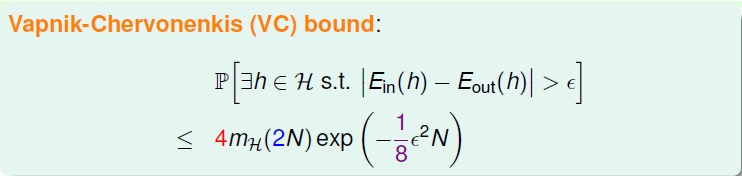
因此,总结一下前面提出的问题:对于2D perceptrons,它的break point是4,那么成长函数mH(N)=O(N^3)。所以,我们可以说2D perceptrons是可以进行机器学习的,只要找到hypothesis能让Ein≈0,就能保证Ein≈Eout。
通过这一讲,我们主要是做了一件事,即证明只要是存在breaking point的,那么它的成长函数mH(N)的上界B(N,K)就是N的K-1阶多项式,故得mH(N)的上界就是N的K-1阶多项式,即学习是可行的。
