
在上一讲,我们主要是做了一件事,即证明只要是存在breaking point的,那么它的成长函数mH(N)的上界B(N,K)就是N的K-1阶多项式,故得mH(N)的上界就是N的K-1阶多项式,即学习是可行的。在前面学习的基础上我们来学习关于VC维的东西。
在前几讲中,我们将机器学习归纳为两个核心问题:
1. 当我们的假设空间是有限的,当N足够大时,我们认为任意一个假设g都可以使Eout≈Ein
2. 我们可以通过算法A从中学习到一个合适的g使得Ein≈0
为了阐述上面的两个问题,证明只要是存在breaking point的,那么它的成长函数mH(N)的上界B(N,K)就是N的K-1阶多项式,故得mH(N)的上界就是N的K-1阶多项式,即有Eout≈Ein。这一将从VC Dimension来看Ein和Eout之间的关系。
上一讲我们得到如下的公式,当我们的成长函数存在一个breaking point的K时,就存在一个一个bounced function的上界,同样它的上界就是N的K-1阶多项式。

从下表我们可以看出N^k-1要比B(N,K)松弛一些,我们可以将值以表格的形式列出来,那么公式就转换成了如下的形式

那么当在数据集满足一定的条件后,我们就将VC bound转换为如下的公式(不理解转换的可以看上一讲的内容),最后我们的不等式就只和数据集的大小N和breaking point 的值K有关。通常在实际情况下,数据N假设是足够多的,所以我们就只用考虑K的值。

故可以得到如下的结论:若我们说的好的假设是指成长函数mH(N)存在breaking point的值K,好的数据集是指N是足够大的,如果满足这两个条件我们可能会得到泛化的Eout≈Ein,再如果有一个好的学习算法A可以找到一个g使得Ein足够的小,那么我们的学习就可能是可行的了。当然在上面的所有条件都满足的情况下,还要一点好的运气哦。
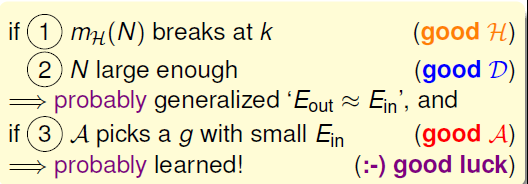
那么什么是VC Dimension呢?VC Dimension就是某假设集H能够shatter的最多输入的个数,即最大完全正确的分类能力。其中shatter的意思比如:如果在k=2时,N个点能划分成2^N中dichotomy时,我们就说是可以被shattered。下面就是VC Dimension的定义:假设集不能被shatter任何分布类型的inputs的最少个数。则VC Dimension等于break point的个数减1,即dvc = minimum k -1。

故当N小于等于dvc时,那么假设空间中存在N个点可以被shattered;如果K>dvc时,K就是假设空间的一个breaking point,那么肯定就不能被shattered。

所以我们可以说,当N>=2,dvc>=2,成长函数值的上界就可以写成N^dvc。
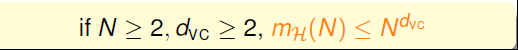
再看一下前面提到过的四个例子有关VC Dimension的相关:我们可以根据关于它的定义给出dvc的值如第二张图。

那么就可以用dvc代替K,那么VC bound的问题也就转换为与dvc和N相关了。同时,如果一个假设集H的确定了,则就能满足机器能够学习的第一个条件,与演算法A、样本数据分布P和目标函数f都没有关系。

学习的流程图就如下所示了

接下来我们看一下二维感知器,下面从两个角度来看一下。假设数据集是了线性可分的,那么PLA就是可收敛的,在T足够大的情况下,就可以找到一个g 使得Ein(g) = 0;或者是当数据集满足一定的概率分布并且存在一个f,使得yn =f(Xn),例如当dvc=3时,当N足够大时,可以得到Eout(g)≈Ein(g),综上,就可以得到Eout(g)≈0,说明我们呢学习到东西了。那么在多维情况下,dvc又是多少呢?PLA是否还可以正常呢?

在1D情况下,dvc=2,2D情况下,dvc=3,那么猜测在d维情况下,dvc=d+1是否成立呢?

要证这个式子成立,我们要从两个方面来证,即

首先先想办法证第一个式子。在d维里,我们只要找到某一类的d+1个输入可以被shatter的话,那么必然得到第一个式子。所以我们有意构造一个d维的矩阵X能够被shatter就行。X是d维的,有d+1个输入,每个输入加上第零个维度的常数项1,得到X的矩阵如下:

X矩阵中,每一行代表一个输入,每个输入是d+1维的,共有d+1个输入。这里构造X的很明显是可逆的。shatter的本质是假设空间H对X的所有情况的判断都是对的,即总能找到权重W,满足XW=y,有W=X^-1y 。由于这里我们构造的矩阵X的逆矩阵存在,那么d维的所有输入都能被shatter,也就证明了第一个不等式。

接下来来证第二个等式,在d维里,如果对于任何的d+2个输入,一定不能被shatter,则不等式成立。我们构造一个任意的矩阵X,其包含d+2个输入,该矩阵有d+1列,d+2行。这d+2个向量的某一列一定可以被另外d+1个向量线性表示,例如对于向量Xd+2,可表示如下,其中假设a1>0,a2…ad<0:
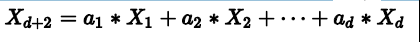
那么如果是X1是正类正类,其余的均为负类,则存在W,得到如下表达式:

因为其中蓝色项大于0,代表正类;红色项小于0,代表负类。所有对于这种情况,Xd+2一定是正类,无法得到负类的情况。也就是说,d+2个输入无法被shatter。证明完毕!

当我们数据写成矩阵后行数多于列数时,我们的数据就会存在线性相关的关系,其中的任意的一个数据都可以用其他的数据表示,其中的系数ai不全为0。


综上我们就可以证明我们的猜想是正确的。
上面的证明中我们提到的W可以被称为自由度,它是可以像旋钮一样任意调节的。故我们呢讨论的VC Dimension代表了假设空间的分类能力,即反映了H的自由度,对于输入产生dichotomy的数量,也就等于features的个数,但也不是绝对的。

我们再看一下前面提到的两个例子,在第一个例子中,我们的dvc=1,自由参数个数为1,第二个例子中,dvc=2,自由参数个数=2,

根据上面的分析,我们就可以得到以下的结论,这里我们可以看出是一种正比的关系。

在前面学习到:当我们假设很少时,根据Hoeffding不等式知,这时不好的事情发生的概率相应的就很小,我们可以满足第一个问题,但是同时我们可以选择的假设太少,可能无法满足第二个问题;当我们的假设很多时,第一个问题可能没法解决,但是足够多的假设总可以找到一个解决第二个问题。从中我们就可以看出,M在这两个核心的问题中起着很重要的作用。
反应到dvc上,我们可以这样说,当我们的dvc很小时,坏事情发生的概率可能会很小,但是这样话我们的Ein就可能不会很小;反之当我们的dvc很大时,坏事情发生的概率可能会变大一些,但是假设的能力会更强,所以使用合适的dvc是很重要的事情。

接下来再深入的学习VC Dimension。首先我们将前面的式子转换成如下所示的样子,我们认为坏事情发生的概率≤δ。

接下来将其反向的转换成如下的样子,其中的ε表示H的泛化能力,值越小泛化能力越大。

到这一步我们可以得到Eout(g)的一个信赖区间,展开绝对值可以得到如下的形式,将根号下的东西称为模型复杂度的惩罚项,可以看到它和三个变量有关。

一般我们只关注上界是怎么样的,所以我们就可以说:在大概率的情况下,Eout(g)的上界如下所示:
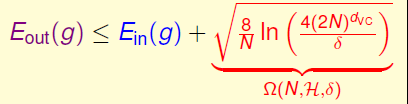
接着还可以看一下Eout、模型复杂度和Ein随dvc的变化:

通过上面的分析我们可以得到以下的结论:
1. dvc越大,Ein就会越小,但是模型复杂度会上升;
2. dvc越小,模型复杂度会下降,但是Ein却越来越大
3. 认为最好的dvc是在变化的中间
通过上面的分析我们得出,当我们在将Ein减小时,如果盲目的增大dvc,可能Ein会按我们的想法下降,但是模型的复杂度随着会增加,将导致我们的Eout增大。故我们在实际中要选择合适的dvc,将成本控制好,这是很重要的!

下面再引入一个新名字Sample Complexity,样本的复杂度。在一些参数固定后,我们在不同的N的情况下,带入公式就可以得到不同的bound function的值,通过分析,我们可以得到在理论上我们的N和dvc的关系大概是10000倍。但是在实际的使用中,我们有时得不到那么多的样本,或者不需要这么多,大概10倍的dvc就够了。

之所以得到10000这样的值,是因为我们的VC Bound过于宽松了,故得到的值远大于实际中我们需要使用的值。

为什么我们的VC Bound是比较宽松的呢?因为我们不关心数据的分布、目标函数,可以使用任何的资料等。值得一提的是,VC Bound是比较宽松的,而如何收紧它却不是那么容易,这也是机器学习的一大难题。但是,令人欣慰的一点是,VC Bound基本上对所有模型的宽松程度是基本一致的,所以,不同模型之间还是可以横向比较。从而,VC Bound宽松对机器学习的可行性还是没有太大影响。

总结一下这一讲学到的东西,听到我还不是全懂,后面再找一下关于VC维的东西来加强一下学习。

参考:第七讲
补:
在理解VC维前要先明白一个词:shatter。对于一个指示函数集,如果存在h个数据样本能够被函数集中的函数按所有可能的2^h种形式分开 ,则称函数集能够把h个数据样本打散(shatter)。函数集的VC维就是能打散的最大数据样本数目h。
例如在下面的图中,当我们有三个点时,无论点是如何分布的,我们总可以找到一条直线,将o和×分开,那么就可以说在二维平面上,任意的三个点都是可以被shattered。

但是当是四个点的时候,我们就不一定可以找到一条直线将其很好的分割开,故VC维就是3
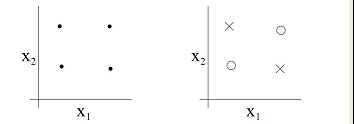
因此我们呢给出VC维的定义:假如存在一个h个样本的样本集能够被一个函数集中的函数按照所有可能的2^h种形式分为两类,则称函数集能够把样本数为h的样本集打散(shattering)。指示函数集的VC维就是用这个函数集中的函数所能够打散的最大样本集的样本数目。也就是说,如果存在h个样本的样本集能够被函数集打散,而不存在h+1个样本集能够被函数集打散,则函数集的VC维就是h。如果对于任意的样本数,总能找到一个样本集能够被这个函数集打散,则函数集的VC维就是无穷大。
VC维反映了函数集的学习能力,VC维越大则学习机器越复杂,所以VC维又是学习机器复杂程度的一种衡量。
找到一篇讲的很好的博文,有兴趣的可以看一下:VC维与学习理论(VC Dimensions And Learning Theory)