Recap and Preview

在前面的一讲中讨论了Feasibility of Learning,即什么时候机器学习是可行的。我们认为机器学习是一种概率可行的问题,如果我们有足够多的统计数据以及有限个假设,我们总认为可以找到一个满足现有数据的最好的假设,这样我们就认为机器学习是可行的。
下面主要学习了Why can machines learn?为什么机器是可以学习的。

承接前面我们呢引入的两个符号Eout和Ein,
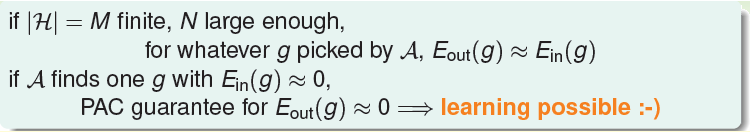
如果我们的假设的数量是有限的,并且数据个数N足够大,我们总可以通过学习算法找到一个g,使得Eout(g)约等于Ein(g)。如果学习算法可以找到一个g使Ein(g)约等于0,那我们在概率意义上可以保证Eout约等于0,这时就是所谓的学习是可以进行的。那么我们的机器学习的流程图为

我们的学习目标就如右下角所示。
首先我们回顾一下之前所学过的内容,结合我们现在学习的内容来看一下

在批处理和有监督的二分类问题中,我们的目标是找到 一个g,希望接近于数据真实的f,即希望Eout(g)约等于0;我们的实现手段就是使Eout(g)约等于Ein(g),并且使得Ein(g)约等于0。
这时我们的学习就转换成了下面的两个问题

1.我们能否确保Eout(g)可以足够的接近Ein(g)?
2.我们能否使得Ein(g)足够的小呢?
同时我们要考虑一下,前面提到的M(即假设的个数)在这两个问题中起到了什么作用呢?

通过分析我们可以得出这样的结论:当我们呢假设很少时,根据Hoeffding不等式知,这时不好的事情发生的概率相应的就很小,我们可以满足第一个问题,但是同时我们可以选择的假设太少,可能无法满足第二个问题;当我们的假设很多时,第一个问题可能没法解决,但是足够多的假设总可以找到一个解决第二个问题。从中我们就可以看出,M在这两个核心的问题中起着很重要的作用,当我们的M是无穷大时将会是个咋样的情形呢?这里提出了一个问题,往后寻找答案。
Effective Number of Line

前面我们假设的Hoeffding不等式如上所示,根据前面的分析,我们知道M会影响到它的概率大小。但是当M很大很大时,这个问题是不是就不能解决了呢?其实不然,
在实际情况下我们希望找到一个Mh来代替M,它比M小更贴近实际。

那么M是来自哪里呢?我们在前面的Hoeffding不等式中看到过
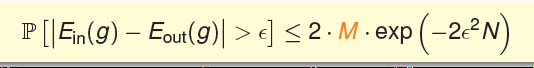
我们说一个假设是不好的时候,是认为它的Eout和Ein相差很大,当差距大于一个阈值,我们就认为它是不好的。为了让我们的学习算法有一个选择的边界,即知道不好的事情发生的总体情况是怎么样的,我们将所有假设发生不好事情的概率使用union bound级联起来,这样就得到了一个不好的事情发生概率上界。那么当每一个概率值都不为0的话,若有无限多个假设时,它的上界就会变得无穷大,这时我们就无法解决问题了?但是真的是这样吗?

在上面的分析中,我们认为每一个假设发生不好的事情是独立的,所以无穷多会导致无限大的发生。但是实际中,不同假设在很多情况下是会有相似的的,也就是他们的范围是会有重叠的。比如在感知机算法中我们划分点时,会有很多的线彼此接近,而且效果是相同的,这是它们就会有重叠的出现。所以我们认为使用级联概率实际上是过度的高估了不好的事情发生的概率。

所以我们需要找到它们重叠的部分,怎么做呢?我们可以将不同的假设就行分类,在同一类别中,假设是相差不多的,即重叠部分是很大的,那么我们的概率值就会变成一个有穷的值,学习就变成了可行的。

下面就来看一下如何进行分类。假设我们只有一个输入X1,这是很简单,我们只能找到两类不同的线,将其分为两种情况。
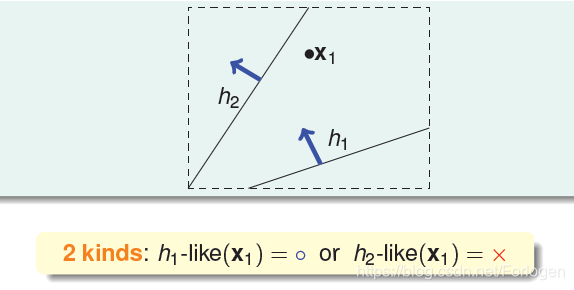
那么有两个输入呢?通过划分我们可以得到以下4种情况。这里我们就会想,一个输入是两种情况,两个输入是四种情况,是不是n个输入的结果就是2^n呢?下面我们再来看一下当有三个输入是什么情况。
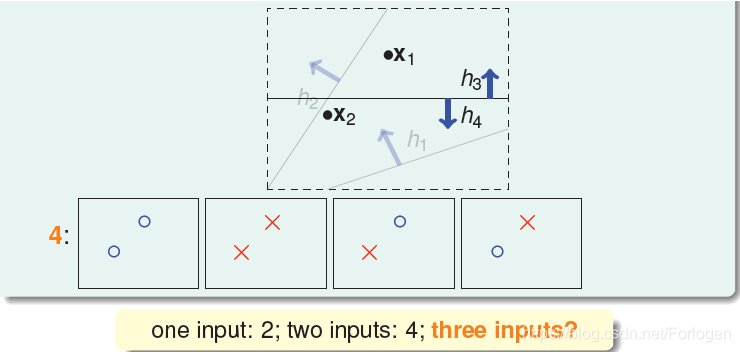
当有三个输入是如下的呈三角分布时,我们可以得到8种情况,这样一看好像我们的猜想是对的哦。但永远是这样吗?
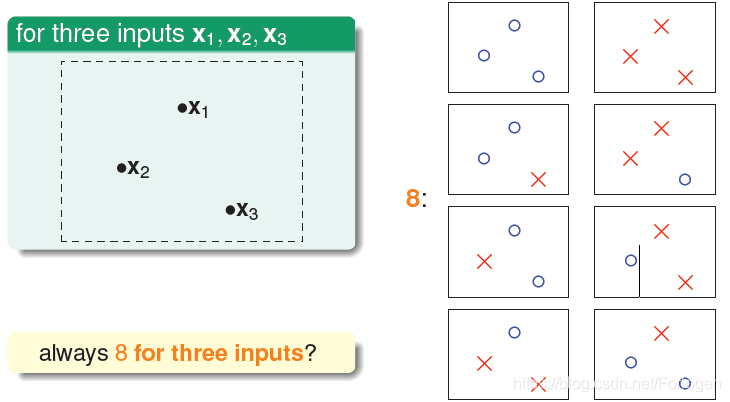
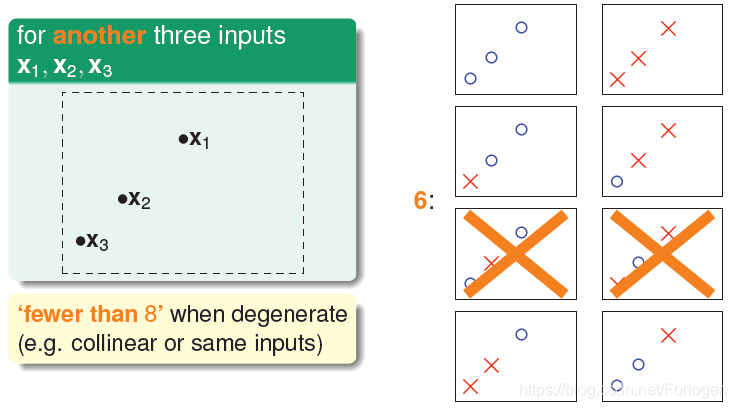
当我们的三个输入是线性排列的时候,我们就可以发现第5和第6种情形不会发生,这样数目就减少了,是个好现象!
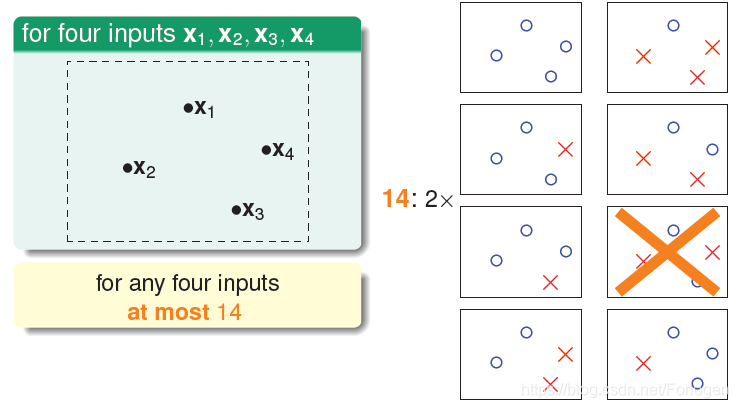
接着我们再看有四个输入是什么情况,通过像前面的分析我们可以得到如下的结果,对于4个输入来说,划分的结果永远最多只有14种,而不是16种。这就说明我们的猜想是不符合实际的。
因此我们呢就可以将上面所提到的最大的数量称为N个输入有效的线的数量,而且它的最大数量是小于等于2^N的。

总结一下前面的四种输入情况,我们得到如下的表格。

有了effective number of lines后,我们的不等式就变成了如下的形式,我们希望使用effective(N)来代替M,并且它的大小远小于2^N,即使M无限大,直线的种类也是有限的,这样不等式右边的概率值就会变得很小,也就是我们可以说不好的事情发生的概率就会很小,在有限的假设(线)中进行学习就成为可能的了。
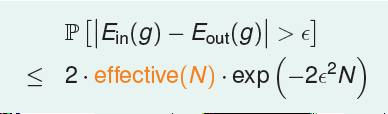
Effective Number of Hypotheses
首先我们呢引入一个新词:二分类(dichotomy),。dichotomy就是将空间中的点(例如二维平面)用一条直线分成正类(o)和负类(x)。


令H是将平面上的点用直线分开的所有hypothesis h的集合,dichotomy H与hypotheses H的关系是:hypotheses H是平面上所有直线的集合,个数可能是无限个,而dichotomy 是平面上能将点完全用直线分开的直线种类,它的上界是。接下来,我们要做的就是尝试用dichotomy代替M。

接着在引入一个新名词:Growth Function(成长函数)。上面我们知道我们的dichotomy依赖于我们的输入,成长函数的定义就是对于N个点组成的不同集合中,某集合对应的dichotomy最大,我们这个值就是dichotomy。它是有限的,而且上界不超过2^N.这里的成长函数值就是我们前面的effective number of lines,只是换了种讲法罢了。
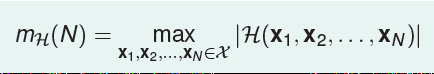
那么我们呢该怎么计算这个值呢?在前面列举的情况中我们可以得到在二维平面上值是这样的情况。

首先我们来看一下一种简单的情况,,我们将所有的点画在一条线上,并且标号从左向右依次增大,我们设定一个值a,将其作为阈值,自然的就会有如下的两种情况。

那么样输入是N个点,就会有N+1段,很容易得到成长函数的值就是N+1。而且N+1远小于2^N,满足我们之前提到的两个问题。

同样的情况,只不过我们的划分情况如下所示

这样做出如下的规定,当位于设定的边界范围中时,我们认为是一类,之外的是另一类。
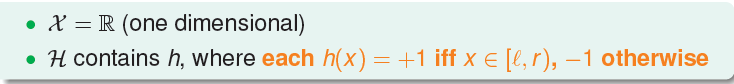
它的成长函数的值可以通过下面的算式求出,并且我们呢可以看出,当N很大的时候,我们的值仍是远小于2^N的,是我们理想中的效果。(下式中的红色的1,,是指当边界范围只是一个点的情况)

接下来我们在看一下非线性的情况。假设在二维空间里,如果hypothesis是凸多边形或类圆构成的封闭曲线,如下图所示,左边是convex的,右边不是convex的。那么,它的成长函数是多少呢?

当数据集D按照如下的凸分布时,我们很容易计算得到它的成长函数值mH = 2^N
这种情况下,N个点所有可能的分类情况都能够被hypotheses set覆盖,我们把这种情形称为shattered。也就是说,如果能够找到一个数据分布集,hypotheses set对N个输入所有的分类情况都做得到,那么它的成长函数就是2^N。

Breaking Point
回顾前面所学的内容,我们一共看到四种成长函数。如下所示,从式子中,我们可以看出前两种的成长函数都是线性的,可以用成长函数的值来代替M,这样得到的情况也是很好的。而convex sets 的成长函数是非线性的,并不能保证学习的可行性。那么,对于2D perceptrons,它的成长函数究竟是polynomial的还是exponential的呢?

这里我们再引入一个新名词:Breaking Point。比如在对于2D perceptrons,我们之前分析了3个点,可以做出8种所有的dichotomy,而4个点,就无法做出所有16个点的dichotomy了。所以,我们就把4称为2D perceptrons的break point(5、6、7等都是break point)。令有k个点,如果k大于等于break point时,它的成长函数一定小于2的k次方。

通过分析,我们呢就可以得出上面四种情况下它们呢各自的breaking point是什么。

通过观察,我们猜测成长函数可能与break point存在某种关系:对于convex sets,没有break point,它的成长函数是2的N次方;对于positive rays,break point k=2,它的成长函数是O(N);对于positive intervals,break point k=3,它的成长函数是O(N^2)。则根据这种推论,我们猜测2D perceptrons,它的成长函数mH =O(N^k-1)。如果成立,那么就可以用代替M,就满足了机器能够学习的条件。但是这种猜测是否正确,还有待我们通过下面的学习进行验证。
Summary
这一篇我们只要学习了机器学习的可行性,我们将其分为了两个核心问题来考虑,并引入了几个新名词辅助我们的分析。然后留下了一个上面所提出的猜测有待解决。
