【林轩田】机器学习基石（五）——训练和测试

Lecture 5 Training versus Testing

ppt
video

Recap and Preview 回顾和预习

Recap

1. 上节课我们讲到了，如果假设空间集是有限的，空间集大小设为$M$；当训练样本数$N$足够大时；对于演算法$A$选择的任何$g$，我们都可以认为$E_{out}(g) \simeq E_{in}(g)$
2. 如果在1的基础上，我们的演算法$A$很幸运地找到一个假设函数$g$，使得$E_{in}(g) \simeq 0$， 我们就可以PAC(probably approximately correct)地说，$E_{out}(g) \simeq 0$， 也就是我们的学习是可行的。
3. 
   如图，在训练阶段，我们希望$E_{in}$误差尽可能小；
   在测试阶段，我们希望$E_{out}$尽量等于$E_{in}$。
   
   前面四节课，
   第一节课简单介绍了机器学习，提出了机器学习的基本组件，这里机器学习的目标是使假设$g$越来越接近目标$f$。
   第二节课老师介绍了一种感知机演算法。这种方法给我们如何在数据$D$中找到误差最小的$g$提供了一种思路。
   第三节课老师介绍了机器学习的不同分类。其中最常见的就是监督二元分类的成批学习，也是我们这段时间课程的学习类型。
   第四节课老师论证了机器学习的可行性。也就是说，在$M$有限的情况下，我们可以PAC地说$E_{out}(g) \simeq E_{in}g)$

所以，我们的学习可以分割成两个核心的问题

1. 我们真的能确保$E_{out}(g)$足够接近$E_{in}(g)$吗？
2. 我们如何让$E_{in}(g)$足够小呢？

在这两个问题中，我们的假设空间集大小$M$又扮演着什么样的角色呢？

当$M$小的话，根据霍夫丁不等式，我们能确保1可以满足的，但是由于$M$过小，选择性太小，所以2不好满足。
当$M$大的话，情况就反过来了。

如此看的话，$M$如果是无限大的，这个显然是不好的。

如果$M$无限大，我们的机器学习就凉凉了！

当然不是这样啦，我们需要在接下来的课程中证明，$M$无限大的时候，机器学习还是有可行性的。

直观的想法是这样的，我们当前看到霍夫丁不等式右半部分的$M$取值是可以无限大的，但是有没有可能，$M$是存在一个有限的上界$m_{H}$的。
也就是说，不管这个空间集$M$，如何变大，在霍夫丁不等式中，我们总可以使得不等式左式小于等于一个有限的由$m_{H}$决定的上界？
当然这只是一个假想，现在还不确定对不对。
但是如果这个假想被证明了，嘿嘿，我们就可以喜滋滋地宣告，机器学习在$M$无限大的时候也是可行的。

Effective Number of Lines 有效的线的种类数量

首先，我们来回顾一下霍夫丁不等式右边的$M$是怎么来的？

$$P[|E_{out}(g)-E_{in}(g)|>\epsilon] \le 2*M*exp(-2N\epsilon^2)$$
左式，代表我们遇到坏的时间 Bad events($B_m$)，即 $|E_{out}(h_m)-E_{in}(h_m)|>\epsilon$， $E_{out}$和 $E_{in}$相去甚远的情况。
右式，使我们使用 union bound计算之后得到的边界，考虑的是，所有的 Bad event都不重合的情况：

当$M$无穷大时，右式的加法也会无穷大，这样霍夫丁不等式就无边界了。

实际上，当假设$h_1 \simeq h_2$时，它们的Bad Events也是会重合的。
我们的union bound会过度估计。

考虑到重叠，我们可以按类别对相似的假设进行分组吗？

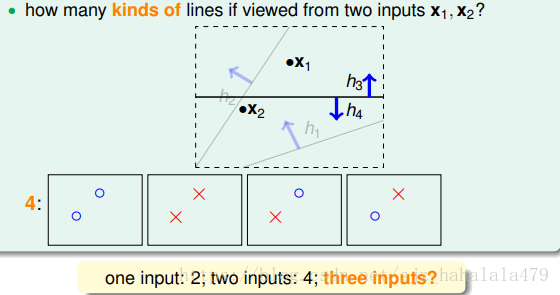
先考虑平面上的二维直线这个简单的例子。

$$H = \{all l\quad ines \quad in \quad R^2\}$$

一共有无数条直线。

当只有1个输入向量时，可以把直线分为两类。一类直线把$x_1$划分为圈圈，一类把$x_2$划分为叉叉。

当只有2个输入向量时，可以把直线分为四类。

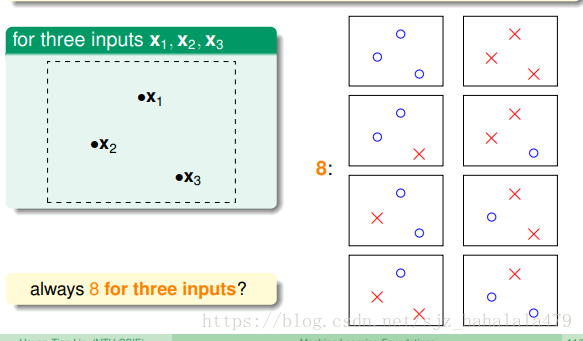
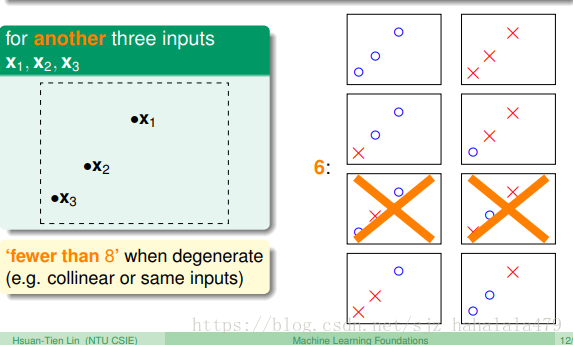
当有三个输入向量时，可以分为小于等于8类直线。

所以，我们无限条线可以被分为不超过$2^N$个种类的线。
所以，就我们的二维直线案例而言，霍夫丁等式右边的$M$可以被替换为$Effective(N)$，且这个$Effective(N)$不超过$2^N$，和右式的其它项乘起来，右式最终的结果是接近0的，哈哈！
这样的话，我们可以说对于无限条直线，机器学习是可行的！

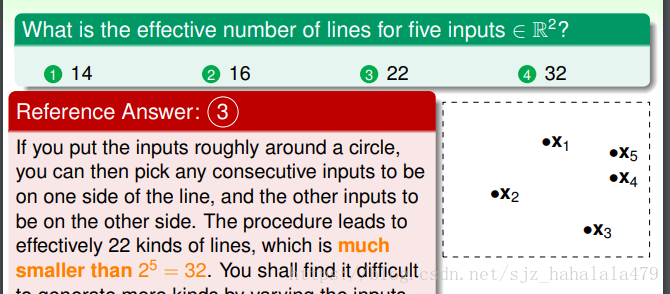
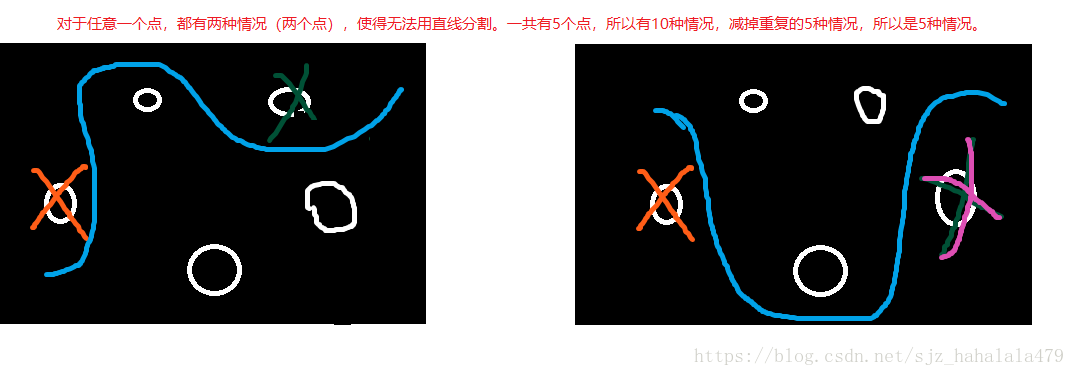
这个问题比较简单，首先5个输入点，上界肯定是$2^5=32$，然后，考虑最极端的情况，$x_1$到$x_5$的分布像一个圆，对于任意一个点$x_n0$，都有两个点$x_n1$，$x_n2$，使得无法用直线分割，计算如下：

$$2*(16-(5*2-2)) = 22$$

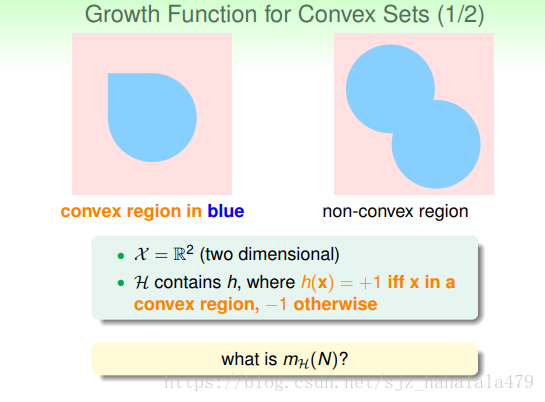
Effective Number of Hypotheses 假设的有效数量

• 现在我们不考虑二维平面上的线，而是考虑抽象的假设。

$$H = \{hypothesis\ h : X \rightarrow \{\times,\circ\}\{$$
假设集中的每个输入 $x$对应的输出都有两种，圈圈或叉叉。

• 根据假设集的输出，我们把这无限多的假设函数限制到有限的种类中去，上界为$2^N$。
  $$h(x_1,x_2,x_3,...,x_n) = (h(x_1),h(x_2),h(x_3),...h(x_n)) \in \{\times,\circ\}^N$$
  每一类都叫做一个dichotomy，即一个二分。
  

我们将二分的集合$|H(x_1,x_2,...,x_n)|$视为M的一个候选。

• $|H(x_1,x_2,...,x_N)|$的大小是依赖于输入$(x_1,x_2,...)$的，要移除二分集合对输入的依赖性，我们选择最极端的情况，即，使得$|H(x_1,x_2,...)|$最大的的输入。
  $$m_H(N) = \max_{x_1,x_2,...,x_N \in X}|H(x_1,x_2,...,x_n)|$$
• 我们把$m_H(N)$叫做成长函数(growth function)，这个成长函数是有限的，上界为2^N。
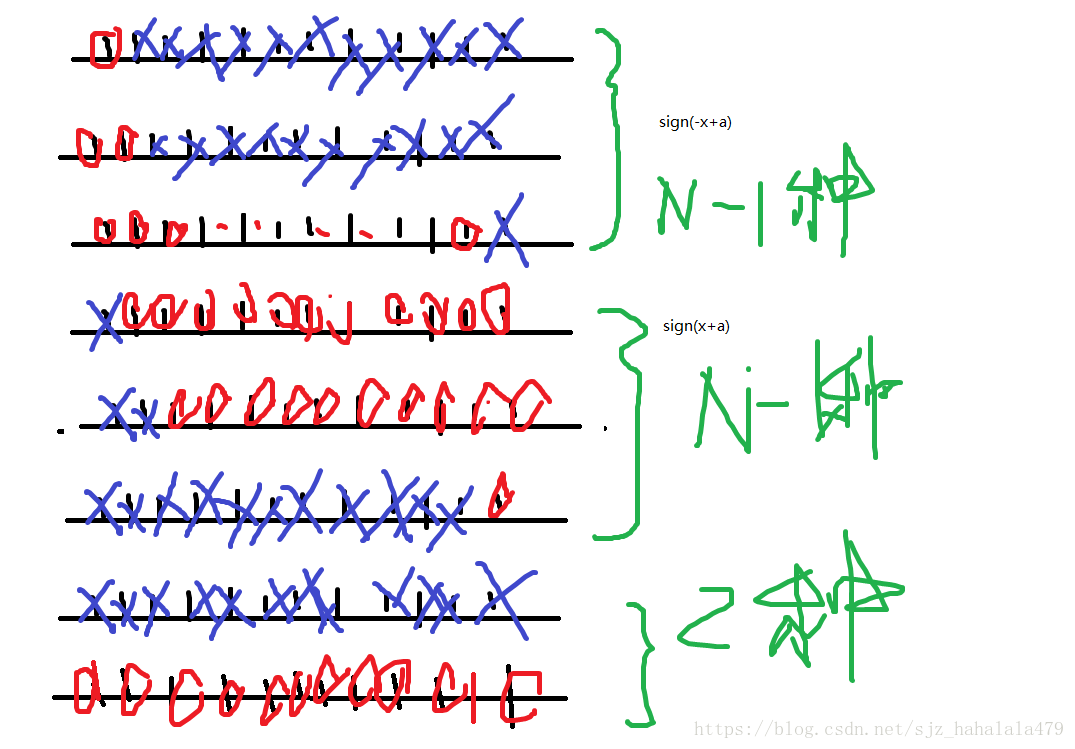
• 那如何计算这个成长函数呢？如下有几种例子。
  

选2N
分析如下：

Break points 断点

对于上节课讲的成长函数，有多项式形式的成长函数，也有指数形式的。
我们希望将$m_H$替代$H$，所以$m_H$的复杂度越低越好。
那么我们可以证明，$m_H(N)$是多项式形式的吗？

这一小节无法给出证明，但是可以引入一个新的概念，断点

什么是断点，当输入的个数$k$不能被$H$打碎时，我们把$k$叫做断点。
我们接下来要研究最小的断点$k$

当存在断点时，也许我们能证明$m_H(N) = O(N^(k-1))$，这样的话，我们就可以说$m_H(N)$在存在断点时是多项式形式的。机器学习就可行啦！！