一:线性回归损失函数的极大似然推导
1:极大似然估计原理:
它是建立在极大似然原理的基础上的一个统计方法,极大似然原理的直观想法是,一个随机试验如有若干个可能的结果A,B,C,… ,若在一次试验中,结果A出现了,那么可以认为实验条件对A的出现有利,也即出现的概率P(A)较大。极大似然原理的直观想法我们用下面例子说明。设甲箱中有99个白球,1个黑球;乙箱中有1个白球.99个黑球。现随机取出一箱,再从抽取的一箱中随机取出一球,结果是黑球,这一黑球从乙箱抽取的概率比从甲箱抽取的概率大得多,这时我们自然更多地相信这个黑球是取自乙箱的。一般说来,事件A发生的概率与某一未知参数 有关, 取值不同,则事件A发生的概率 也不同,当我们在一次试验中事件A发生了,则认为此时的 值应是t的一切可能取值中使 达到最大的那一个,极大似然估计法就是要选取这样的t值作为参数t的估计值,使所选取的样本在被选的总体中出现的可能性为最大。 [1]
极大似然估计,只是一种概率论在统计学的应用,它是参数估计的方法之一。说的是已知某个随机样本满足某种概率分布,但是其中具体的参数不清楚,参数估计就是通过若干次试验,观察其结果,利用结果推出参数的大概值。极大似然估计是建立在这样的思想上:已知某个参数能使这个样本出现的概率最大,我们当然不会再去选择其他小概率的样本,所以干脆就把这个参数作为估计的真实值。
2:极大似然对线性回归损失函数的推导
线性回归假设函数为
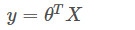
误差:
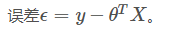
假设误差服从正态分布,误差最小也就是期望为0。ϵϵ~N(0,σ2σ2)
最大似然估计就是使所有样本最接近参数,也就是似然函数最大。

一元线性回归的参数公式求导

三 西瓜书公式3.10和3.11的推导

四,什么是批梯度下降,小批梯度下降,随机梯度下降
批量梯度下降
批量梯度下降是指在对参数执行更新时,在每次迭代中使用所有的样本。
for i in range(num_epochs):
grad = compute_gradient(data, params)
params = params — learning_rate * grad
主要的优点:
-
训练期间,我们可以使用固定的学习率,而不用考虑学习率衰减的问题。
-
它具有朝向最小值的直线轨迹,并且如果损失函数是凸的,则保证理论上收敛到全局最小值,如果损失函数不是凸的,则收敛到局部最小值。
扫描二维码关注公众号,回复: 5087606 查看本文章
-
梯度是无偏估计的。样本越多,标准误差就越低。
小批量梯度下降
为了克服上述方法的缺点,人们提出了小批量梯度下降。在更新每一参数时,不用遍历所有的样本,而只使用一部分样本来进行更新。 因此,每次只用小批量的b个样本进行更新学习,其主要过程如下:
-
打乱训练数据集以避免样本预先存在顺序结构。
-
根据批量的规模将训练数据集分为b个小批量。如果训练集大小不能被批量大小整除,则将剩余的部分单独作为一个小批量。
for i in range(num_epochs):
np.random.shuffle(data)
for batch in radom_minibatches(data, batch_size=32):
grad = compute_gradient(batch, params)
params = params — learning_rate * grad
批量的大小我们可以调整,通常被选为2的幂次方,例如32,64,128,256,512等。其背后的原因是一些像GPU这样的硬件也是以2的幂次方的批量大小来获得更好的运行时间。
主要的优点:
-
比起批量梯度下降,速度更快,因为它少用了很多样本。
-
随机选择样本有助于避免对学习没有多大贡献冗余样本或非常相似的样本的干扰。
-
当批量的大小小于训练集大小时,会增加学习过程中的噪声,有助于改善泛化误差。
-
尽管用更多的样本可以获得更低的估计标准误差,但所带来的计算负担却小于线性增长
随机梯度下降(Stochastic Gradient Descent,SGD)
随机梯度下降法不同于批量梯度下降,随机梯度下降是每次迭代使用一个样本来对参数进行更新。使得训练速度加快。
对于一个样本的目标函数为:
J(i)(θ0,θ1)=12(hθ(x(i))−y(i))2
J(i)(θ0,θ1)=12(hθ(x(i))−y(i))2
(1)对目标函数求偏导:
ΔJ(i)(θ0,θ1)θj=(hθ(x(i))−y(i))x(i)j
ΔJ(i)(θ0,θ1)θj=(hθ(x(i))−y(i))xj(i)
(2)参数更新:
θj:=θj−α(hθ(x(i))−y(i))x(i)j
θj:=θj−α(hθ(x(i))−y(i))xj(i)
注意,这里不再有求和符号
伪代码形式为:
repeat{
for i=1,…,m{
θj:=θj−α(hθ(x(i))−y(i))x(i)jθj:=θj−α(hθ(x(i))−y(i))xj(i)
(for j =0,1)
}
}
优点:
(1)由于不是在全部训练数据上的损失函数,而是在每轮迭代中,随机优化某一条训练数据上的损失函数,这样每一轮参数的更新速度大大加快。
缺点:
(1)准确度下降。由于即使在目标函数为强凸函数的情况下,SGD仍旧无法做到线性收敛。
(2)可能会收敛到局部最优,由于单个样本并不能代表全体样本的趋势。
(3)不易于并行实现。