凸优化第二章凸集 2.4广义不等式

2.4广义不等式

1. 正常锥与广义不等式
2. 最小元和极小元

正常锥

一个锥K是正常锥需要满足以下几个条件：

• K是凸的
• K是闭的
• K是实的，具有非空内部
• K是尖的，不包含直线

广义不等式

用正常锥可以定义广义不等式，即上的偏序关系。

严格偏序关系:

当时，这种偏序关系也就是R上实际的

例子：分量不等式：

矩阵不等式:，半正定。

广义不等式的性质：

1. 对于加法保序：
2. 传递性：
3. 非负数乘保序性：
4. 自反的：
5. 反对称的：
6. 极限运算保序：

最小元和极小元

在介绍极小元和最小元之前，先说明“可比较”的概念，广义不等式中的偏序关系比普通意义的不等式更复杂，在实数域，任意两个数都可比较，但是在广义不等式就未必行得通，比如分量不等式，两个向量x,y，如果x<y，则要求x的每一个分量都小于y的对应分量，如果，x和y就是不可比较的。

最小元

最小元：都有且，则x是S的最小元。

且x是S的最小元，当且仅当，x+K表示与x是可比较的（即可以与x相比）并且大于等于x的所有元素。

极小元

极小元；，则x是S的极小元。

x是S的极小元当且仅当，x-K表示与x是可比较的（即可以与x相比）并且小于x的所有元素。

以为例，下图，分别展示了其最小元和极小元

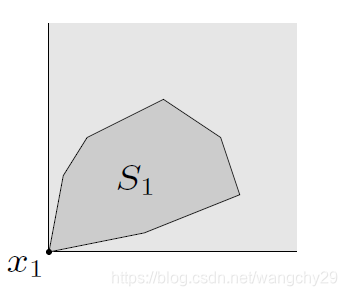
上图为集合的最小元，在中，，以第一分量做水平坐标轴，第二分量做垂直坐标轴，在几何上可以看成是y在x的右上方，即上图浅色阴影区域，同时可以看出。

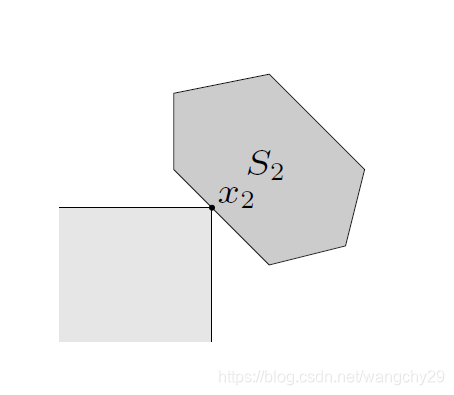
上图展示了的极小元，首先可以看出中的点并不是全部都与可比较，但在中与可比较的全部的点中，最小。

综上两图可以发现S中最小元m和极小元l的异同。

1. 最小元m可与S中全部元素相比较，极小元l不与S中的全部元素可比较（将S中可与极小元l比较的元素集合记为C）。
2. m在S中最小，l在C中最小。