前置知识
导数,矩阵的逆
知识地图

正则化是通过为参数支付代价的方式,降低系统复杂度的方法。牛顿方法是一种适用于逻辑回归的求解方法,相比梯度上升法具有迭代次数少,消耗资源多的特点。
过拟合与欠拟合
回顾线性回归和逻辑回归这两个算法,我们发现特征这个词汇在频繁出现。特征是从不同的角度对事物进行描述,特征数量会决定模型的复杂程度和最终的性能表现。
为了方便讨论,我们通过添加高阶多项式的方法来增加特征数量。原始数据集中只有一个特征,依次添加原始特征的2次方,3次方......直至6次方作为新的特征。
当特征数量不足时会使得模型太简单,模型不能很好地拟合样本。这种情况称为欠拟合,如下图所示:
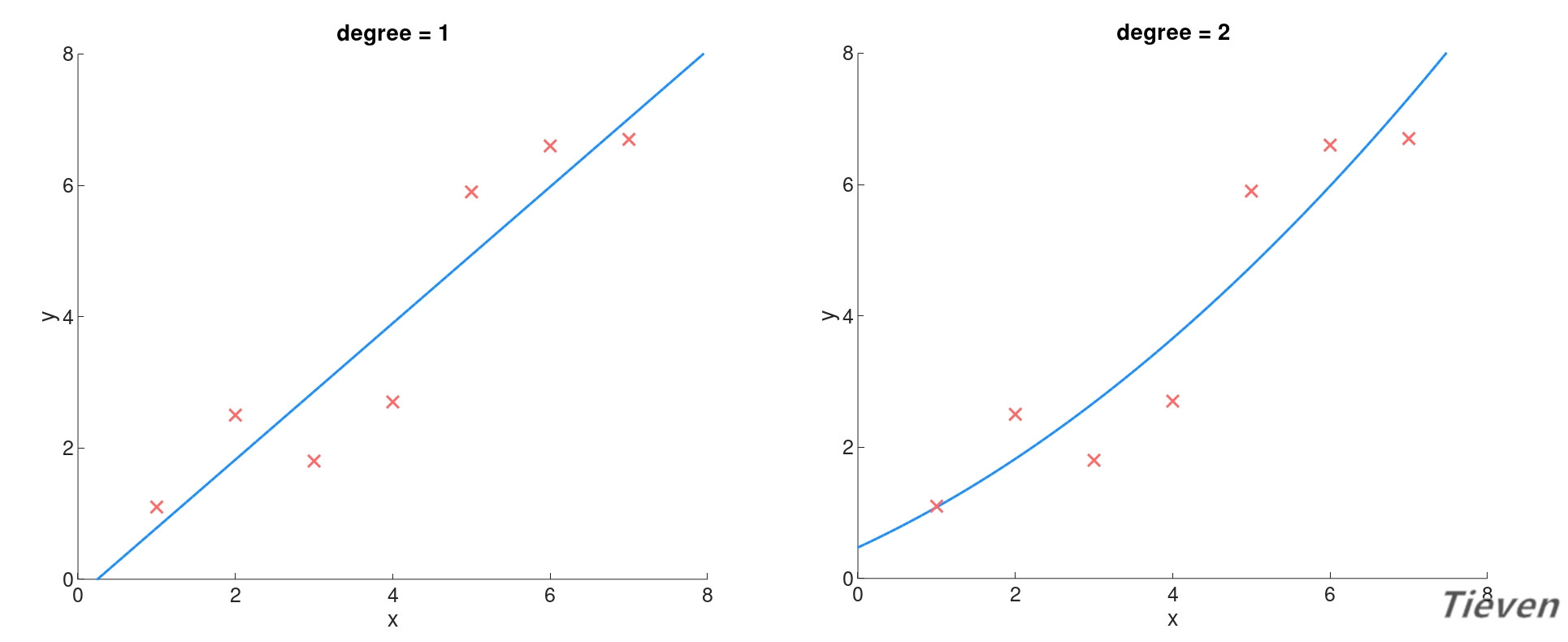
随着特征数量的增加,模型的复杂度也逐渐增加,模型对样本的拟合程度也在逐步提升,如下图所示:

当特征数量过多时会使得模型太复杂,模型可以极好地拟合样本。这种情况称为过拟合,如下图所示:
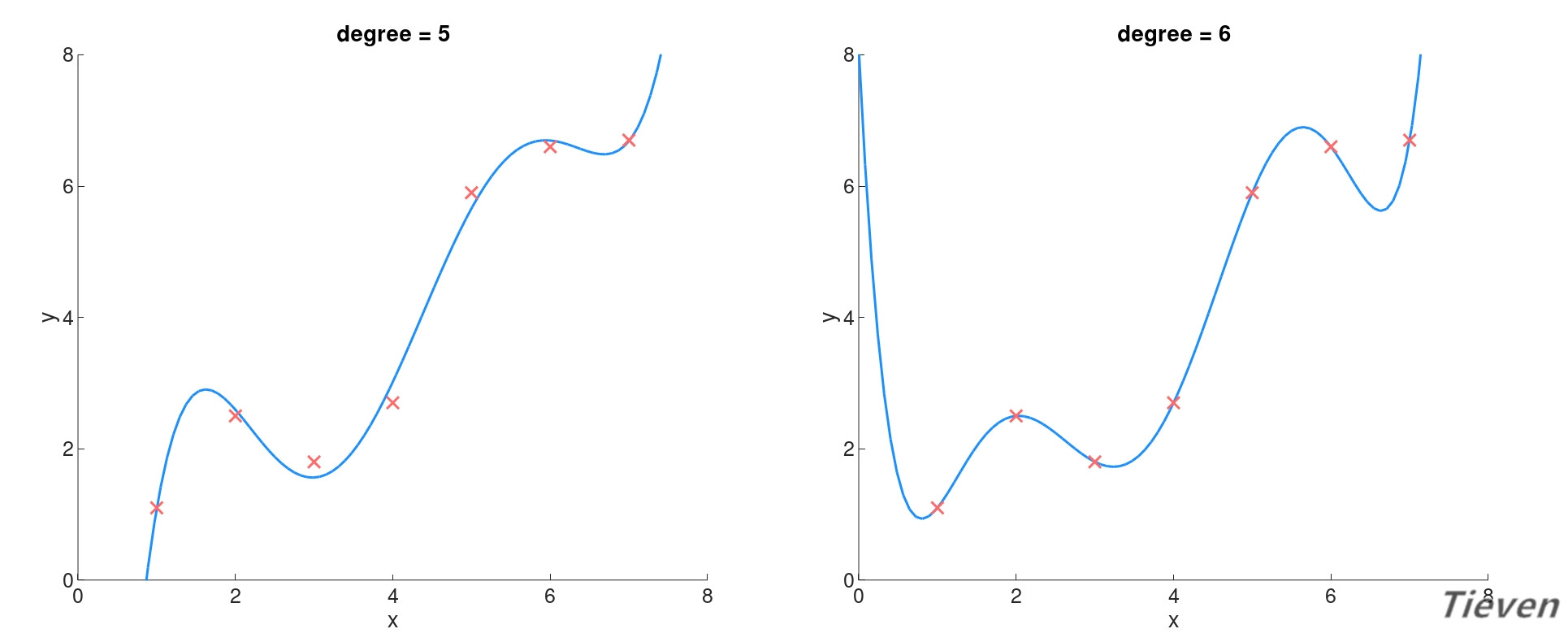
显然欠拟合的情况是不好的,那么过拟合的情况如何呢?虽然模型很好地拟合了数据集,然而这不是一个好的模型,它对数据集过度拟合以至于对新样本的泛化能力很差。
“如无必要,勿增实体”。参数是特征的权重,当参数越大时特征的影响越大,当参数越小时特征的影响越小。如果能让参数尽量变小,就可以降低模型的复杂度。
为了避免出现过拟合的情况,可以在代价函数中加入正则化项,正则化项是关于参数的代价。因为存在代价,算法在寻找全局最优点的过程中,必须使得参数尽量最小化。
正则化
线性回归原代价函数如下:
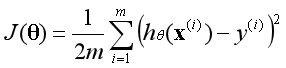
线性回归新代价函数如下:
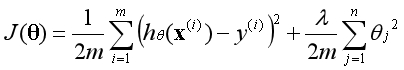
λ称为正则化参数,和学习率α一样,这是一个需要手动调节的参数。正则化参数λ的作用是调节以下两个目标间的平衡关系:
目标一:使模型更好地拟合数据;
目标二:使参数θ尽量最小化;
当正则化参数λ减小时,需要为参数θ支付的代价变小,模型的复杂度提高,存在的风险是可能会出现过拟合。
当正则化参数λ增大时,需要为参数θ支付的代价变大,模型的复杂度降低,存在的风险是可能会出现欠拟合。

注:1/2是为了后续求导的方便;
正则化项的含义是,平均每个样本需要为参数支付的代价,代价以参数平方的形式体现。数据集中原本有n个特征,加入一列全为1的常数项后一共有n+1个特征,对应n+1个参数。
下图为特征相同的情况下,当正则项参数不同时模型的变化。随着正则项参数增大,需要为参数所支付的代价增大。为了最小化代价函数,必须降低特征的权重,进而简化了模型。

以下为对应的参数:

注意j是从1开始算起的,也就是说,常数项对应的参数θ0不参与正则化。这是理解和实践中很容易混淆的地方,下面用对比图说明这样约定的原因。
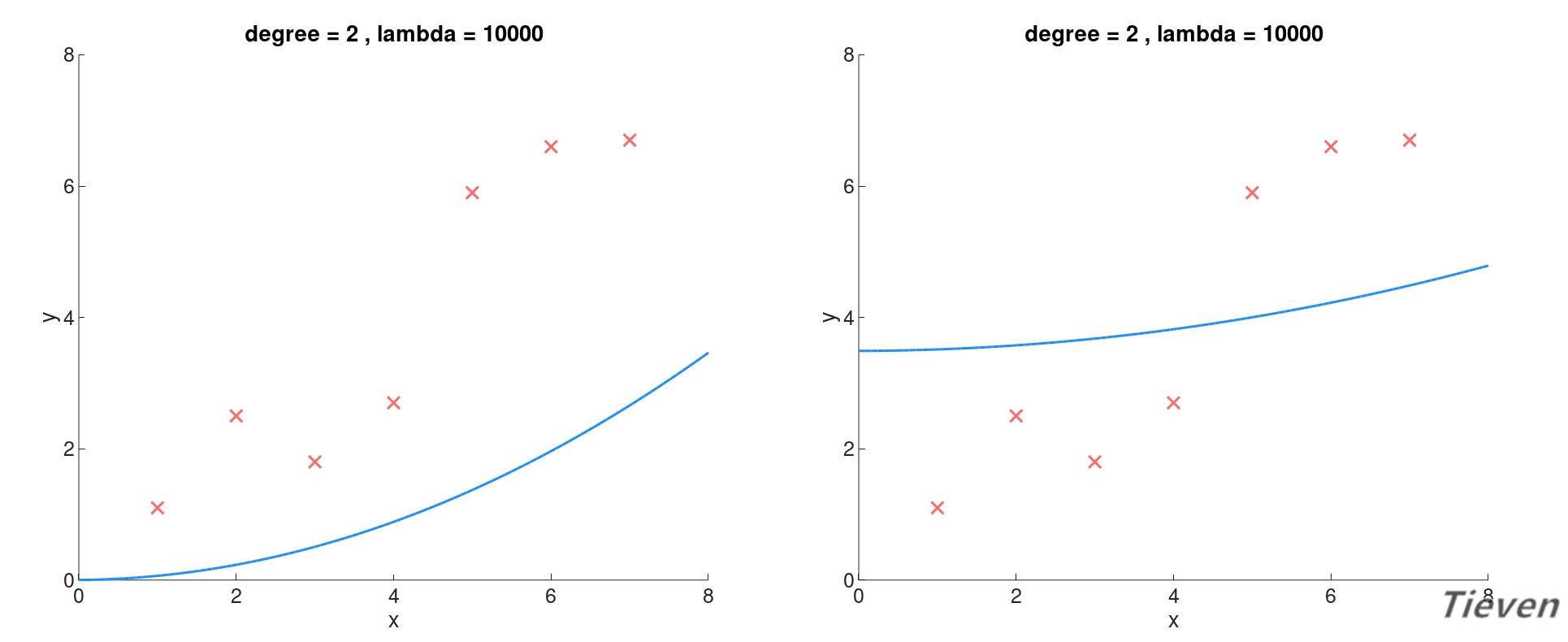
左图为所有参数都参与正则化的结果,因为正则化参数非常大,为了最小化代价函数,所有的参数都趋向于0。模型是经过原点的曲线,无法体现出样本的平均水平。
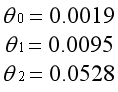
右图为θ0不参与正则化的结果,因为正则化参数非常大,为了最小化代价函数,除了θ0外的参数都趋向于0。虽然模型的表现也很差,至少体现出样本的平均水平。
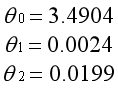
注意在理论说明时向量的下标是从0开始计数,在代码编写时向量的下标是从1开始计数。向量θ中的第一个元素即常数项对应的参数,这个元素不参与正则化。
将线性回归的函数更新如下:
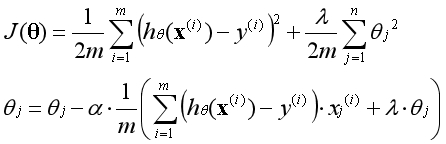
将逻辑回归的函数更新如下:
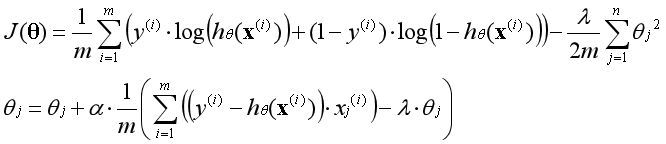
函数与导数
当函数只有一个变量时,在二维空间中可以表现为一条曲线。假设函数在f(θ)=0处有解,已知导数是切线的斜率,根据这一点可以寻找到函数在该点的解。
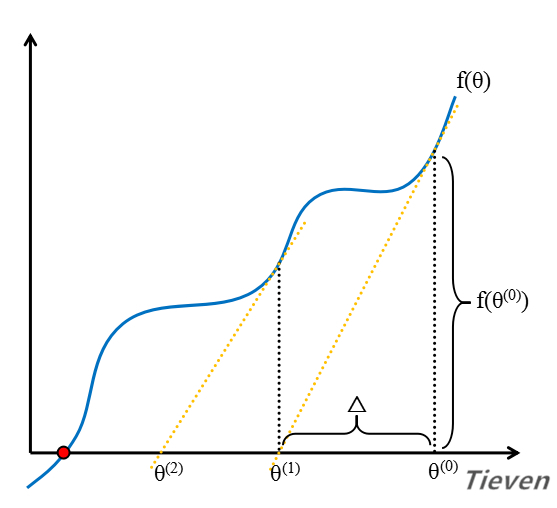
首先随机选择一个初始值作为第一个交点。
求出函数在第一个交点的导数,将切线延长到x轴上,可以得到第二个交点。
求出函数在第二个交点的导数,将切线延长到x轴上,可以得到第三个交点。
在这个过程中,交点在不断地向目标靠近。如此反复,最终得到函数在f(θ)=0处的解。单变量的牛顿法迭代形式如下:
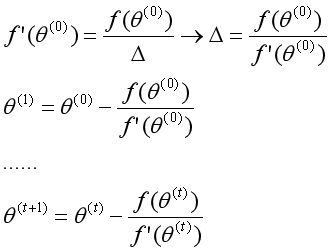
牛顿方法
这个方法如何应用到逻辑回归算法中?当一阶导数为0时,函数处于极值点。要求代价函数的最优解,可转化为求一阶导数为0,这又可通过牛顿方法用二阶导数进行迭代。
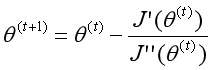
所以问题的关键在于如何求代价函数的二阶导数。因为代价函数中有多个变量,每个变量都有相对于其他变量的二阶偏导数。这些二阶偏导数表现为矩阵的形式,以两个变量为例。

右边的符号表示第j个变量相对于第i个变量的二阶偏导数。虽然形式复杂,但本质上在求一个变量的偏导数时,是直接将其他变量视为常数,这就极大地简化了问题。
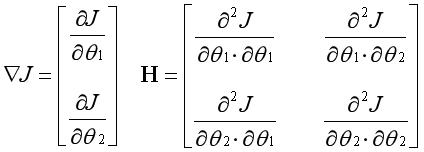
左边是一阶导数向量,右边是二阶导数矩阵(Hessian Matrix),多维下的牛顿方法可表示为以下形式:
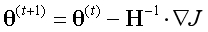
逻辑回归一阶导数:
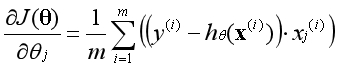
逻辑回归二阶导数:
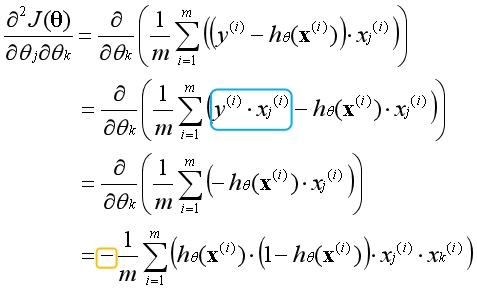
蓝色部分相对于变量是常数项可以直接消去,等式最外面有一个负号不要遗漏了。现在的问题是该如何得到整个二阶导数矩阵呢?构造一个小规模的样本观察一下规律。
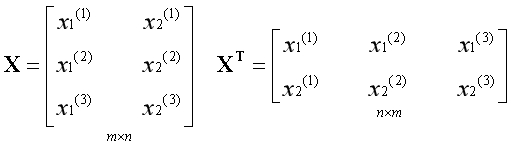
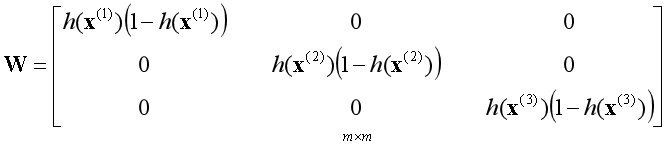
假设j=1,k=2,将对应的二阶偏导数函数展开:
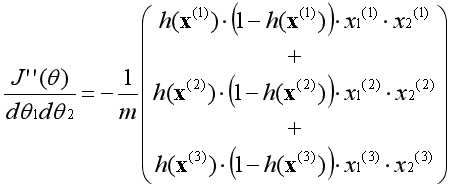
观察上式,发现只有一种矩阵的组合方法满足要求,即:
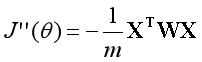
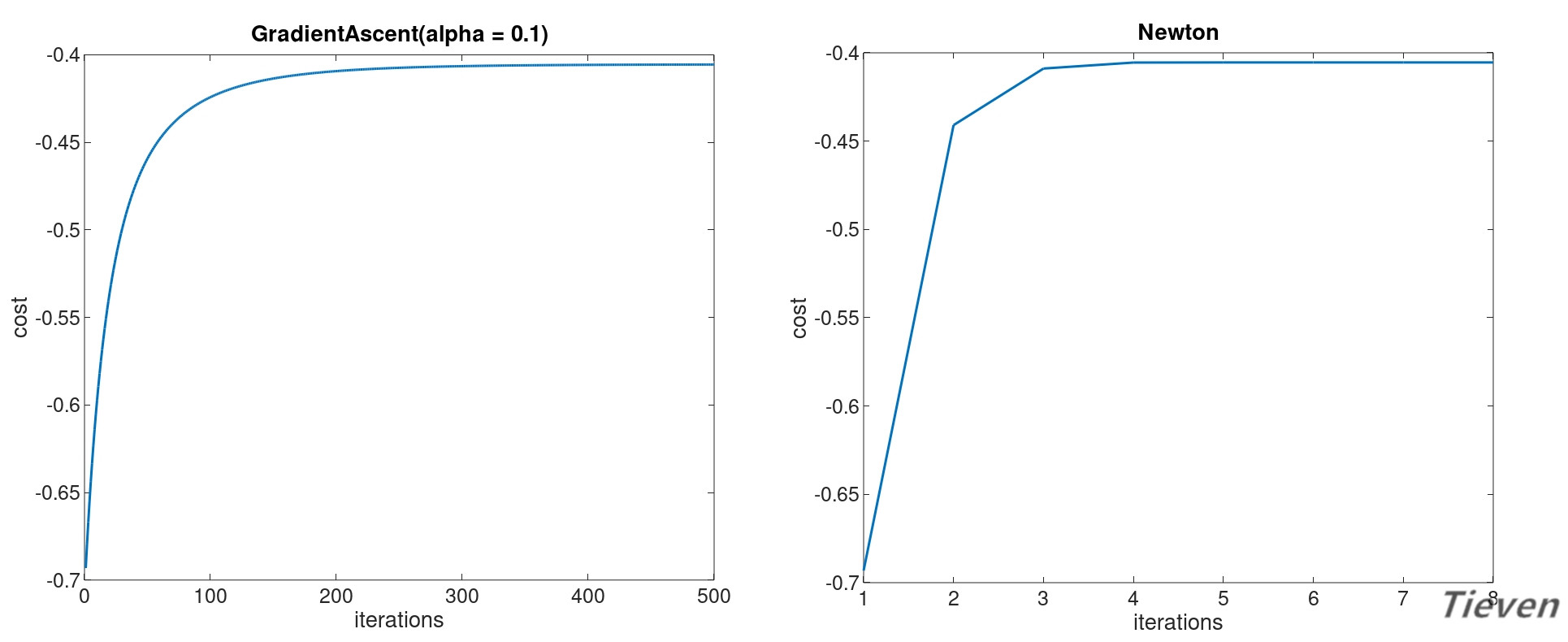
相比梯度上升法,牛顿方法的优点是不需要设置学习率,且所需迭代次数远远少于前者。缺点是需要计算二阶导数的逆矩阵,为避免求逆又衍生出了许多的改良版本。
总结
正则化通过为参数支付一个代价,使得参数尽量最小化。参数是特征的权重,当权重降低的时候,特征对于模型的影响也随之降低。当模型复杂度降低时,往往能获得更好的表现。
牛顿方法是通过二阶导数来更新参数的方法,在大规模机器学习问题中,求解二阶导数的逆矩阵难以实现,实际中常用的是伪牛顿法,如BFGS,L-BFGS等等。
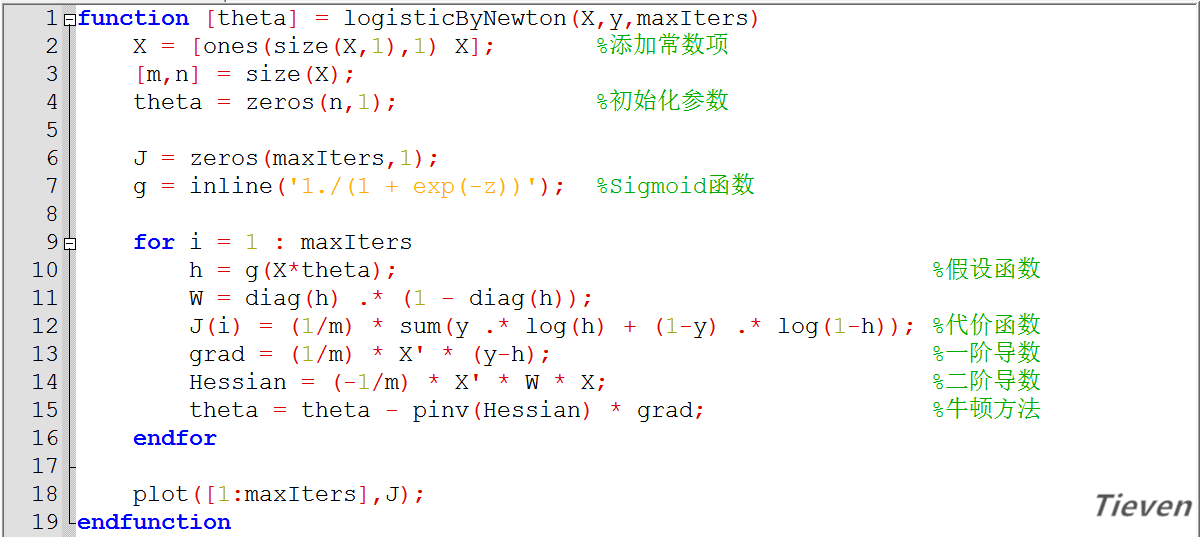
非正规代码

版权声明
1,本文为原创文章,未经作者授权禁止引用、复制、转载、摘编。
2,对于有上述行为者,作者将保留追究其法律责任的权利。
Tieven
2019.1.9