损失函数正则化方法

正则化方法

为防止模型过拟合，提高模型的泛化能力，通常会在损失函数的后面添加一个正则化项。L1正则化和L2正则化可以看做是损失函数的惩罚项。所谓【惩罚】是指对损失函数中的某些参数做一些限制

L1正则化(ℓ1 -norm)

使用L1正则化的模型建叫做Lasso Regularization(Lasso回归),直接在原来的损失函数基础上加上权重参数的绝对值， $\eta$为正则化参数：
假设损失函数为 $\tag{1}J_0=\sum_{i=1}^{m}(y^{(i)}-\theta_0-\theta_1X_1^{(i)}-\theta_2X_2^{(i)}-\cdots-\theta_nX_n^{(i)})$则Lasso Regularization为：
$\tag{2}J=J_0+\eta \sum_{i=1}^{m}|\theta|$
$J$ 是带有绝对值符号的函数，因此 $J$是不完全可微的。当我们在原始损失函数 $J_0$后添加 $L_1$正则化项时，相当于对 $J_0$做了一个约束。令 $L_1=\eta\sum_{i=1}^{m}|\theta|$，则 $J=J_0+L_1$，此时我们的任务变成在 $L$约束下求出 $J$取最小值的解。
$\eta$ 被称为正则化系数.

下面通过图像来说明如何在约束条件 $L_1$下求 $J$的最小值。

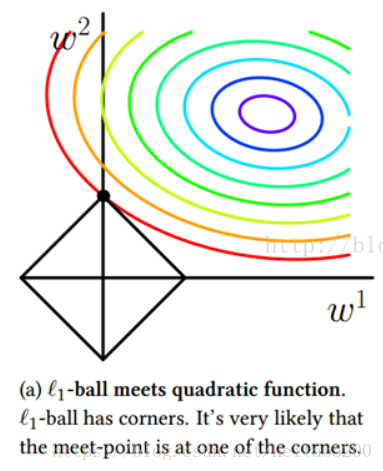
最终的损失函数就是求等高圆圈+黑色黑色矩形的和的最小值。由图可知等高圆圈+黑色黑色矩形首次相交时， $J$取得最小值。
为什么 $L_1$正则化项能够防止过拟合的情况？
对损失函数的参数优化求解过程进行分析
$\tag{3}\frac{\partial C}{\partial \theta}=\frac{\partial C_0}{\partial \theta}+\lambda sgn(\theta)$

上式中 $sgn(\theta)$表示 $\theta$的符号。那么权重 $\theta$的更新规则为:
$\tag{4}\theta \rightarrow \theta - \eta\sum_{i=1}^{m} \frac{\partial C_i}{\partial \theta}-\eta \lambda sgn(\theta)$

比原始的更新规则多出了 $η λ sgn(\theta)$这一项。当 $\theta$为正时，更新后的 $\theta$变小。当 $\theta$为负时，更新后的 $\theta$变大——因此它的效果就是让 $\eta$往0靠，使网络中的权重尽可能为0，也就相当于减小了网络复杂度，防止过拟合。

L2正则化(ℓ2 -norm)

使用L2正则化的模型叫做Ridge Regularization（岭回归）,直接在原来的损失函数基础上加上权重参数的平方和：
令损失函数为 $J_0$，则Ridge Regularization为：
$\tag{5}J=J_0+\frac{1}{2}\eta \sum_{i=1}^{n}\theta^2$
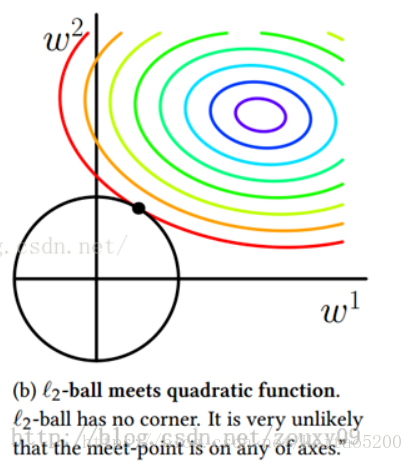
使最终的损失函数最小，要考虑 $J_0$和 $\tag{6}L_2=\frac{1}{2}\eta \sum_{i=1}^{n} \theta^2$两个因素，最终的损失函数就是求等高 圆圈+黑色圆圈的和的最小值。由图可知两个圆相交时， $J$取得最小值。

为什么 $L_2$正则化项能够防止过拟合的情况？
对损失函数的参数优化求解过程进行分析
$\tag{7}\frac{\partial C}{\partial \theta}=\frac{\partial C_0}{\partial \theta}+\lambda \theta$

$\tag{8}\frac{\partial C}{\partial b}=\frac{\partial C}{\partial b}$
可以发现L2正则化项对b的更新没有影响，但是对于 $\theta$的更新有影响:
$\theta \rightarrow \theta - \eta\sum_{i=1}^{m} \frac{\partial C_i}{\partial \theta}-\eta \lambda \theta$

$\tag{9}=(1-\eta \lambda )\theta - \eta \sum_{i=1}^{m}\frac{\partial C_i}{\partial \theta}$

在不使用L2正则化时，求导结果中 $\theta$前系数为1，现在 $\theta$前面系数为 $1−ηλ$ ，因为η、λ都是正的，所以 $1−ηλ$小于1，它的效果是减小 $\theta$，这也就是权重衰减（weight decay）的由来。