运筹优化（五）--线性规划之内点法

近年来的内点算法主要有三大类：

（1）投影尺度法,它是Karmarkar算法的原型。这个方法要求问题具有特殊的单纯形结构和最优目标值为零,在实际计算过程中, 需要用复杂的变换将实际问题转换为这种标准形式。因此, 投影尺度法在实际中应用较少。

（2）仿射尺度法，这是一种已经比较成熟和广泛的算法。目前原仿射尺度法和对偶仿射尺度法虽然应用较多,但这两种方法的多项式时间复杂性还不能从理论上得到证明。

（3）路径跟踪法,又称为跟踪中心轨迹法。这种方法将对数壁垒函数与牛顿法结合起来应用到线性规划问题, 并且已经从理论上证明具有多项式时间复杂性。路径跟踪法收敛迅速, 鲁棒性强, 对初值的选择不敏感,现在已经被推广应用到二次规划领域,正被进一步发展为从复杂性角度研究一般非线性规划的内点算法,是目前最有发展潜力的一类内点算法。

内点法是求解不等式约束最优化问题的一种十分有效方法，但不能处理等式约束。因为构造的内点惩罚函数是定义在可行域内的函数，而等式约束优化问题不存在可行域空间，因此，内点法不能用来求解等式约束优化问题。

投影尺度法

核心原理：

针对线性规划的标准型：

$min(max)\, \, c \cdot x$

$s.t.\: \: \: \: \: \: Ax = b \, \, \, \, \, \, \, x \geq 0$

改进最快的移动方向是目标函数向量 $\Delta x = c$ ,方向d在条件 $A\Delta x = 0$ 上的投影，使得线性约束Ax = b成立，得到：

$\Delta x = Pd$

其中P是投影矩阵： $P = (I - A^{^{T}}(AA^{T})^{-1}A)$

仿射尺度变换

仿射尺度变换采用最简单的策略远离边界，通过对模型进行重复尺度变换使当前解的变形与所有不等式约束距离相等。

仿射尺度变换之后，采用上面投影矩阵，计算改进方向。移动步长是向量d的长度倒数。

算法不断重复尺度变换，在投影方向上移动改进，计算新的可行解，直到目标函数值变化差异稳定。

障碍函数法（Barrier Method）

参考：https://zhuanlan.zhihu.com/p/32685234

障碍函数思想的内点法主要思想是：在可行域的边界筑起一道很高的“围墙”，当迭代点靠近边界时，目标函数徒然增大，以示惩罚，阻止迭代点穿越边界，这样就可以将最优解“档”在可行域之内了。

约束优化算法的基本思想是：通过引入效用函数的方法将约束优化问题转换成无约束问题，再利用优化迭代过程不断地更新效用函数，以使得算法收敛。这句话，可以用下面的推导来说明：

对于下面的不等式约束的优化问题：
$\min f(x), x \in R^n$

$s.t \quad g_{i}(x) \leq0, i=1,2,...,m$

利用内点法进行求解时，构造惩罚函数的一般表达式为
$\varphi (X, r)=f(X)-r\sum_{i=1}^{m}\frac{1}{g_{i}(X)}$

或者
$\varphi (X, r)=f(X)-r\sum_{i=1}^{m}{\ln[-g_{i}(X)]}$

也就是通过这一步，将约束（ $\quad g_{i}(x)$ ）优化问题转化为无约束（ $\varphi (X, r)$ ）优化问题，然后就是一个迭代逼近的，求极值的优化问题了。

更一般的表述：

线性规划问题的一般形式为：

这个线性规划问题可以重新表述为计算：

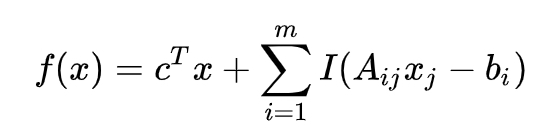
这里，我们使用了一个indicator函数，定义为：

引入这个函数的意义在于可以将约束条件直接写入到目标函数里面，这样我们直接求新的函数的极小值就可以了，而不必借助于未知乘子。但是这里有一个问题，那就是indicator函数存在不可求导的点，因此在求函数极小值的时候我们没法通过普通的微分法来确定函数的极小值。为了规避这个问题，我们可以用一个光滑的函数来近似这个indicator函数。一个不错的选择是用：

来代替indicator函数。上式只有在u < 0的时候有定义，我们规定当u > 0的时候上式为正无穷，而且参数t > 0越大，函数Itu就越接近于Iu. 所以我们可以通过调节t的值来调节这个函数的近似程度。使用这个近似的indicator函数，我们新的的目标函数可以写作 :

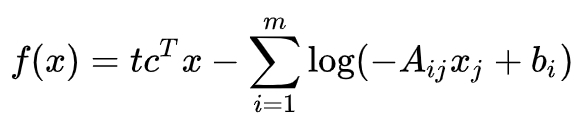
因为线性函数是凸函数，并且indicator也是凸函数，所以fx是凸函数，因此我们可以很容易用凸优化的经典方法得到该函数的极小值。
算法步骤，
取初始惩罚因子 $r^{(0)}>0$ ，允许误差 $\epsilon>0$ ；
在可行域D内选取初始点X(0)，令k=1；
构造惩罚函数φ(X,r(k))，从X(k−1)点出发用无约束优化方法求惩罚函数φ(X,r(k))的极值点(X∗,r(k))；
检查迭代终止准则：如果满足
$\|X^{*} r^{(k)}-X^{*} r^{(k-1)}\|\leq\epsilon_{1}=10^{-5}-10^{-7}$
或者
$\|\frac{\varphi (X^{*} ,r^{(k)})-\varphi (X^{*}, r^{(k-1)})}{\varphi (X^{*}, r^{(k-1)})}\|\leq\epsilon_{2}=10^{-3}-10^{-4}$
则停止迭代计算，并以(X∗,r(k))作为原目标函数f(X)的约束最优解，否则转入下一步；
取r(k+1)=cr(k)，X(0)=X∗r(k)，k=k+1，转向步骤3。递减系数c=0.1−0.5，通常取0.1。

内点惩罚函数法特点及其应用

惩罚函数定义于可行域内，序列迭代点在可行域内不断趋于约束边界上的最优点（这就是称为内点法的原因，只适合求解具有不等式约束的优化问题
内点法求解案例
用内点法求下面约束优化问题的最优解，取迭代初始X0=[0,0]T，惩罚因子的初始值r0=1，收敛终止条件 $\|X^k - X^{k-1}\| \leq \varepsilon$
$\varepsilon = 0.01$
$\min f(X) = x_1^2 + x_1^2 - x_1x_2 - 10x_1 - 4x_2 + 60$
构造内惩罚函数： $\varphi(X, r) = x_1^2 + x_1^2 - x_1x_2 - 10x_1 - 4x_2 + 60 -r\ln(x_1 + x_2 -8)$
用解析法求内惩罚函数的极小值
$\nabla\varphi(X, r) = [2x_1 - x_2 - 10 - \frac{r}{x_1 + x_2 - 8} \quad 2x_2 - x_1 - 4 - \frac{r}{x_1 + x_2 - 8}]$
令∇φ(X,r)=0得： $\begin{align}2x_1 - x_2 - 10 - \frac{r}{x_1 + x_2 - 8} = 0 \\ 2x_2 - x_1 - 4 - \frac{r}{x_1 + x_2 - 8} = 0\end{align}$
解得：

$X^*_1(r) = \begin{bmatrix}\frac{13 + \sqrt{9+2r}}{2} & \frac{9 + \sqrt{9+2r}}{2}\end{bmatrix}^{\mathrm{T}}$
∵g(X∗1(r))>0
∴ 舍去X∗1(r)
∵φ(X,r)为凸函数

∴无约束优化问题的最优解为 $X^*(r) = X^*_2(r) = \begin{bmatrix}\frac{13 - \sqrt{9+2r}}{2} & \frac{9 - \sqrt{9+2r}}{2}\end{bmatrix}^{\mathrm{T}}$
求最优解
当r0=1时， $X^*(r^0) = \begin{pmatrix}4.8417 & 2.8417\end{pmatrix}^{\mathrm{T}}$ , $\|X^*(r^0) - X^0\| = 5.6140 > \varepsilon$
当r1=0.1时， $X^*(r^1) = \begin{pmatrix}4.9834 & 2.9834\end{pmatrix}^{\mathrm{T}}$ , $\|X^*(r^1) - X^*(r^0)\| = 0.2004 > \varepsilon$
当r2=0.01时， $X^*(r^2) = \begin{pmatrix}4.9983 & 2.9983\end{pmatrix}^{\mathrm{T}}$ , $\|X^*(r^2) - X^*(r^1)\| = 0.0211 > \varepsilon$
当r3=0.01时， $X^*(r^3) = \begin{pmatrix}4.9998 & 2.9998\end{pmatrix}^{\mathrm{T}}$ ， $\|X^*(r^3) - X^*(r^2)\| = 0.0021 < \varepsilon$
即X∗(r3)为最优解

原始对偶内点法（Primal Dual Interior Point Method）

下面一堆公式，不理解的化只要记住：

原始对偶内点法始终保持原始问题和对偶问题的解在每次迭代中严格可行，并在搜索过程中系统性的减少互补松弛性的违背程度。其难点在于最优条件中的互补松弛约束，除非当前解最优，否则会存在对偶间隙，迭代的目的在于不断减少当前的互补松弛结果与目标差异。
在 Primal Dual 的方法中，我们直接考虑一个标准的 LP 命题。
$\min c^Tx, \quad \text{subject to } Ax=b, x\ge0 \tag9$
它的对偶命题为：
$\max b^T\lambda, \quad \text{subject to } A^T\lambda +s=c,s\ge0 \tag{10}$
上面两个命题的KKT条件为：
$\begin{align} A^T\lambda+s&=c, \tag{11a} \\ Ax&=b, \tag{11b} \\ x_i s_i &= 0, i=1,...,n\tag{11c} \\(x,s) &\ge0.\tag{11d} \end{align}$
为了后面的推导方便，将上面的KKT条件化为矩阵形式如下：
$\begin{align} F(x,\lambda,s)=\begin{bmatrix} A^T\lambda+s-c\\ Ax-b\\ XSe\end{bmatrix} &= 0. \tag{12a} \\ (x,s)&\ge 0, \tag{12b}\end{align}$
其中，
$X=\text{diag} (x_1,x_2,...,x_n),\quad S=\text{diag} (s_1,s_2,...,s_n), \quad e = (1,1,...1)^T$
如同一般的优化算法，这里需要定义一个量来检验当前的迭代点与最优点的差距。在Barrier Method中，使用 duality gap 的上界 $\frac mt$ 来检验的，在 Primal Dual Method 中，我们定义一个新的 duality measure 来进行某种衡量：
$\mu=\frac 1n\sum_{i=1}^nx_is_i=\frac{x^Ts}n$
注意：这里的 μ与 Barrier Method 中的 μ 意义不同，为了与各自书中的表达方式对应，分别选用了各自书中的变量记法。
要求解原始的优化命题，需要做的就是去求解 (12) 这样一个方程组，由于 F 阵第三行中 XS 一项的存在，因此这是一个非线性系统。要求解这样一个非线性系统，一种实用的方法就是牛顿法。（注意，这里说的牛顿法是一种求解非线性方程组的方法，与求解优化命题的牛顿法并不完全一样，但核心思路是一致的，都是在迭代点处进行二阶展开。）在当前点处求解一个前进方向，并通过迭代逼近非线性系统的解。
$J(x,\lambda,s) \begin{bmatrix} \Delta x\\ \Delta\lambda \\ \Delta s\end{bmatrix}=-F(x,\lambda,s)$
其中 JJ 是FF 阵的雅各比矩阵。我们将 FF 阵中的前两行分别记为：
$r_b=Ax-b,\quad r_c=A^T\lambda+s-c \tag{13}$
那么在每次迭代中需要求解的线性系统为：
$\begin{bmatrix} 0 &A^T &I \\ A & 0 & 0 \\ S & 0 &X \end{bmatrix}\begin{bmatrix} \Delta x\\ \Delta\lambda \\ \Delta s\end{bmatrix}=\begin{bmatrix} -r_c \\ -r_b \\ -XSe\end{bmatrix}$
因此，在求解得到相应的前进方向后，需要做的就是求解确定一个步长 α 来进行如下的更新
$(x,\lambda,s)+\alpha(\Delta x, \Delta\lambda, \Delta s)$
其中 α∈(0,1] 的选取要使得原始变量和对偶变量都满足相应的约束。
看起来这种方法似乎已经可以了，但通过这种被称为 affine scaling direction 的方向所得到的 α 往往很小。也就是说，很难在迭代中取得进展。一开始看到这个说法时，我也很难理解这句话的意思。所以在这里我们用一个图来说明，令 (9) 中的 $c = \p\begin{bmatrix} 10 \\ \\ 1\end{bmatrix}$ ，初始点为(0.7,2)，这里不考虑等式约束，直接采用affine scaling direction 的方向得到的迭代点的轨迹为

从图中可以看出，几乎在从第二次迭代开始，迭代点就一头撞上了约束。后面的迭代也只能贴着约束的边缘来走，因为要保迭代点不能违反约束，因此每次的步长 α 都只能取得很小。在这一过程中，一共进行了11次迭代才使得 duality measure μ<10−5。
因此，实际上内点法采用的是一个不那么 aggressive 的牛顿方向，也就是控制迭代点使其徐徐想约束边界和最优点处靠近。具体的方法是，我们在用牛顿法求解非线性系统时，在每次迭代中并不要求直接实现 xisi=0，而是令其等于一个逐渐减少的值，具体来说就是 xisi=σμ，其中 μ 是当前的 duality measure，σ∈[0,1]是用于控制下降速度的下降因子。也就是说，在每次迭代中要求解的方程组应该是
$\begin{bmatrix} 0 &A^T &I \\ A & 0 & 0 \\ S & 0 &X \end{bmatrix}\begin{bmatrix} \Delta x\\ \Delta\lambda \\ \Delta s\end{bmatrix}=\begin{bmatrix} -r_c \\ -r_b \\ -XSe+\sigma\mu e\end{bmatrix} \tag{14}$
其中，σ 被称为 center parameter 。意在表示我们要通过调整 σ 使得迭代点的轨迹在 central path 附近。
Central Path
在内点法中，central path 是指满足下面一组方程式的迭代点所组成的所组成的一条弧线
$\begin{align}A^T\lambda+s&=c,\tag{15a} \\ Ax&=b,\tag{15b} \\ x_is_i&=\tau, i=1,2...n. \tag{15c} \\ (x,s)&>0 \tag{15d}\end{align}$
这与 (11) 中的KKT 条件的区别就在于在第三个条件的等式右端的 0 被 τ>0 替代了。
也就是说，对偶内点法的基本思路就是依据 central path 计算出相应的方向，并控制步长 α 的选择使得迭代点位于 central path 的某一个邻域内。

关于步长 α 的选取，central parameter σ 的更新，以及更多的收敛性分析的内容，在这里不作展开。

举例
与上一张图对应，我们同样取 c=(10 1)，初始点为(0.7,2)，不考虑等式约束。采用对偶内点法的迭代点的轨迹为

可以看出，引入 central path 后，迭代点能在贴近约束边界后再次远离约束边界（也就是靠近 central path），从而保证下一次迭代能取得更大的进步。在这一过程中，一共进行了6次迭代就使得 duality measure μ<10−5。