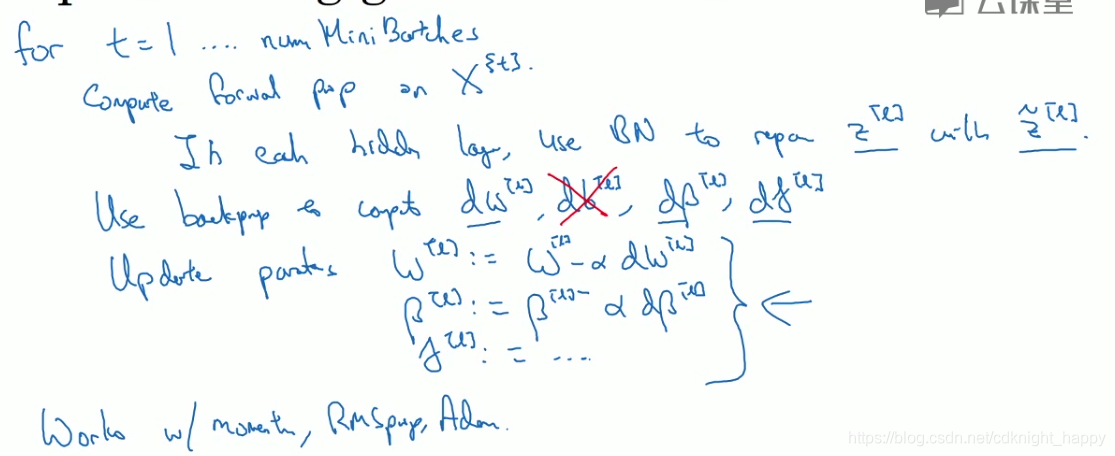deeplearning.ai第二课第三周：超参数调试、BN层

版权声明：本文为博主原创文章，未经博主允许不得转载。 https://blog.csdn.net/cdknight_happy/article/details/85268255

1 超参数调试

不同的超参数有不同的重要程度。比如，学习率一般最重要，momentum中的 $\beta$值、隐藏单元数量、mini-batch的size次之，隐藏层的数量、权重衰减规则更次之。至于Adam中，一般都是用 $\beta_1 = 0.9,\beta_2 = 0.999,\epsilon = 10^{-8}$的默认值。

1.1 超参数筛选的两个准则

正因为不同的超参数的重要程度不同，因此进行超参数筛选时不建议进行有规则的网格化筛选，而是建议进行随机筛选。举例，假如要筛选的超参数1为最重要的学习率，超参数2为Adam中的 $\epsilon$参数，这样对于不同的 $\epsilon$而相同的学习率的一组实验，实验结果都是非常接近的，因此，网格化的筛选会造成大量的实验浪费。正确的做法是进行随机筛选，这样就可以对比较重要的超参数进行更多组的实验。

另外一个超参数筛选的准则是进行从粗到精的筛选，比如超参数的筛选过程以0.01为粒度，分别筛选初始学习率为[0.01,0.02,0.025,0.036]的参数，经过多次验证实验发现初始学习率为0.02的效果最好。此时，应该进行更加细粒度的筛选，比如从[0.015,0.017,0.018,0.019,0.021,0.023]中筛选最优超参数。

1.2 超参数的筛选范围

某些超参数，均匀取值是比较合适的，比如隐藏层的单元数量可以在[50,100]的范围内均匀取值、隐藏层数量可以在[2,5]的范围内均匀取值。

对于学习率参数，其取值范围可能是[0.0001,1]，若采用均匀取值，即取值为0.0001，0.0002，…0,0.0009,0.001,0.0011,…,1，这样会有90%的点落在[0.001,0.01]的范围内。此时，应该采用对数域上的搜索。即将数据轴均匀分为0.0001，0.001，0.01，0.1，1五个点。然后在各区间内部进行均匀取点。用python实现为：r = -4 * np.random.rand(), $\alpha = 10^{r}$。

指数加权平均中的参数 $\beta$，表示是前 $\frac{1}{1 - \beta}$个值的加权平均，其取值应该设置 $1 - \beta$在对数域取值，从而确定 $\beta$的值。

之所以设置在对数域取值，是因为在某些区域参数的变化对算法的影响更大。

超参数设置实战：
如果计算资源有限，可以仔细照看模型的训练过程，适当调整超参数；
如果拥有充足的计算资源，可以一次训练很多不同超参数的模型，从中选取最合适的。

2 Batch Normalization

2.1 对输入进行归一化

实现过程：减均值、除标准差
$u = \frac{1}{m}\sum_{i=1}^{m}x^{(i)}$
$x^{(i)} = x^{(i)} - u$
$\sigma^2 = \frac{1}{m}{x^{(i)}}^2$
$x^{(i)} /= \sigma^2$

效果：
将损失函数的形状由长的峡谷状调整为近似圆形，这样有助于通过迭代算法快速收敛到函数的最优解，避免迭代过程在峡谷的两侧反复震荡。

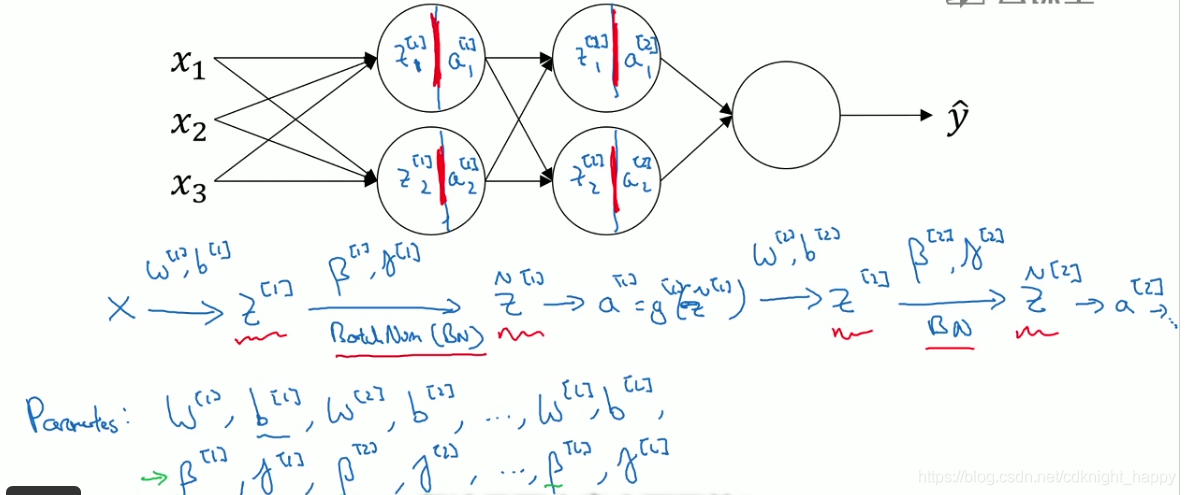
2.2 BN

BN就是对神经网络的每一个隐藏层都进行归一化操作，使得各网络层的训练过程更加高效。比如，我们可以对神经网络的 $a^{[2]}$进行归一化，从而使得 $W^{[3]},b^{[3]}$的训练更加高效。实践中，一般是将BN放在relu之前，因此，我们会对 $Z^{[2]}$进行BN操作，再使用relu激活函数。

实现过程：
给定神经网络第 $l$ 层的输入 $Z^{[l](i)}$， $i \in (1,m)$。
$u = \frac{1}{m}Z^{[l](i)}$
$\sigma^2 = \frac{1}{m}{Z^{[l](i)} - u}^2$
$Z^{[l]}_{norm} = \frac{Z^{[l]} - u}{\sqrt{\sigma^2 + \epsilon}}$
$\hat{Z^{[l]}} = \gamma^{[l]} Z^{[l]}_{norm} + \beta^{[l]}$

$\gamma和\beta$是训练过程中引入的两个超参数。

在神经网络中使用BN层：

$\beta^{[l]},\gamma^{[l]} \in R^{n^{[l]} \times 1}$。

有一个细节要注意:
$Z^{[l]} = W^{[l]}a^{[l - 1]} + b^{[l]}$
如果使用BN层，则进行减均值操作时， $b^{[l]}$都会被抵消，所以，在应用BN层的神经网络中，可以暂时忽略参数 $b^{[l]}$。

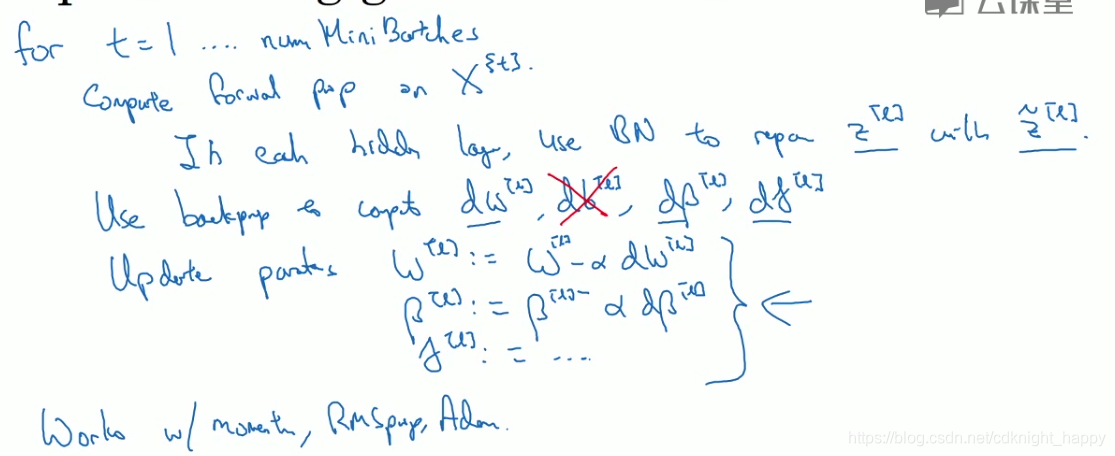
一般BN是应用在mini-batch上的，减的是mini-batch的均值，除的是mini-batch的方差。

为什么BN会生效？
对隐藏层应用BN，会限制该隐藏层前面层的数据变化对当前层的输入的影响程度。因为，无论前面的层怎样变化，当前层都会对数据进行归一化操作再使用 $\gamma$和 $\beta$进行“covariance shift”。BN层减少了输入数据变化造成的影响，使得送入下一层的输入更加稳定。

未使用BN层时，前面层的参数变化，后面层的参数就要做对应的改变，但应用BN层之后，前面参数变化造成的输出变化被BN层进行了减弱，后层参数的变化幅度会减小。因此，BN层减弱了前层参数变化与后层参数变化之间的联系，迫使神经网络的每一层去独立学习，有助于加速神经网络的学习过程。

BN层还起到了一定的正则化效果。这是因为应用BN层时，只是使用当前mini-batch样本计算均值与方差，然后进行归一化操作。而不同的mini-batch计算得到的均值和方差不同，这相当于向训练过程中添加了噪声，迫使各网络层学习更加鲁棒的特征，因此起到了轻微的正则化效果。

应用BN层时，使用的mini-batch越大，添加的噪声越小，正则化效果也就越小。

BN层添加的正则化效果很有限，因此可以将BN层和dropout一起使用。

测试时如何使用BN？
测试时应用BN层，一般是对某一BN层，减去该层在训练过程中所有mini-batch均值的指数加权平均，除的是该层在训练过程中所有mini-batch标准差的指数加权平均。

3 Softmax回归

softmax用于多分类的输出函数，是logistic regression的泛化。其计算过程为：
$a^{[L]} = \frac{\exp(z^{[L]})}{\sum_{j=1}^{n_L}\exp(z^{[L]}_j)}$
上式分子部分为对 $z^{[L]}$进行逐元素的指数运算，最终得到的输出格式为向量，输出向量的各个元素表示输入样本属于各输出类别的概率。

可以理解softmax层的输入为未归一化的对数概率，因此计算过程为先对输入进行指数运算，再进行归一化转换为概率值。

损失函数：
假设输出为C类，则损失函数为： $L(y,\hat y) = -\sum_{j=1}^Cy_j\log{\hat y}_j$。
对于多分类任务，假设当前输入样本的正确类别为第二类，则 $y = \left[ \begin{matrix}0 \\ 1 \\ 0 \\ 0\end{matrix}\right]$，假设得到的预测输出为 $\hat y = \left[ \begin{matrix}0.3 \\ 0.2 \\ 0.1 \\ 0.4\end{matrix}\right]$，则该样本的预测损失为 $l = -\sum_{j=1}^{4}y_j\log \hat y _j = -\log 0.2 = 1.609$。最小化损失函数就等于迫使预测的 $\hat y_2$的值增大，即增大正确类别的预测概率。

对整个训练数据集而言，代价函数为： $J = \frac{1}{m}\sum_{i=1}^{m}L(y,\hat y)$。

softmax的导数：
对于单个样本而言，假设其正确类别为 $i$，则其损失函数为 $-\log \hat y_i = -\log \frac{\exp(z_i)}{\sum_{j=1}^C\exp(z_j)}=\log \sum_{j=1}^C \exp(z_j) - z_i$。

损失函数相对于 $z_i$的梯度为 $\frac{\exp(z_i)}{\sum_{j=1}^C\exp(z_j)} - 1 = \hat{y}_i - 1$；损失函数相对于 $z_j,j \neq i$的梯度为 $\frac{\exp(z_j)}{\sum_{j=1}^C\exp(z_j)} =\hat y_j$。由于 $\hat y$中 $\hat y_i = 1,\hat y_j =0(j \neq i)$，因此损失函数相对于 $z$的梯度可以写为 $\hat y - y$。