引言
上一篇讲到了在有限的hypotheses下,学习错误的发生率,即E_in与E_out不同的概率边界,本篇将会探讨在infinite hypotheses情况下的概率边界。
线的有效数字(Effective Number of Lines)
我们先将学习划分为两个核心的问题,即
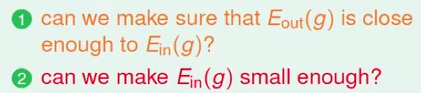
图4.1
设M代表H的大小,对M与上述两个问题之间的关系有如下的结论

图4.2
当M很小的时候,E_in与E_out非常接近,但是由于M很小,所以可供选择的假设空间很小,则E_in不一定很小;而大的M则与之相反。根据Hoeffding Inequality:

图4.3

图4.4
图4.4所展示的是在m个假设空间下的概率边界求解过程,B1~Bm表示m个事件,当m无限大时,是否可以找到一个值来替换图4.3的M?
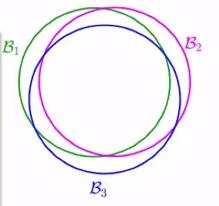
<图4.5>
再来看上图,B1,B2和B3代表了三个近乎重叠的事件,如果按照图4.4将其union bound,则我们又多增加了重叠部分的信息,即会出现over-estimating。这个示例要说明的是,我们在推导有限个H的概率边界时忽略了如hypotheses重叠的情况导致边界变大以致于我们无法估计无限大的事情。这里利用分类的方式来解决上述问题。
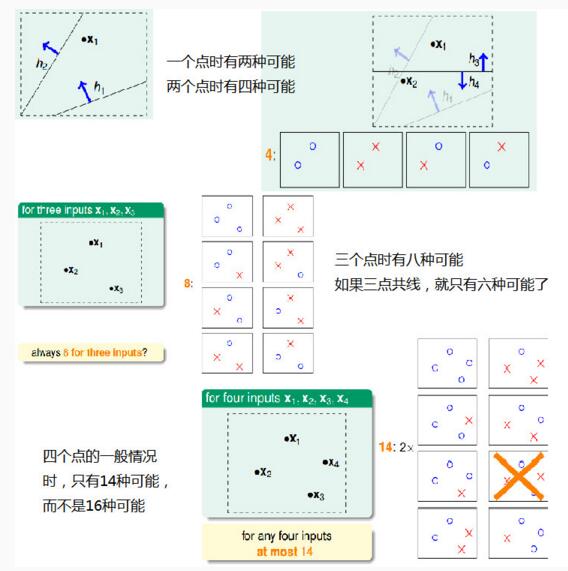
图4.6
我们利用二维空间的线性分类来举例,如图4.6,最终得到当有N个点时,最多可划2^N$条线。

图4.7
上图定义了effective number of lines,即对于N个输入得到的有限的线,结合上例,即effective(N)=2^N$,将其普遍的形式代入Hoeffding Inequality,得到
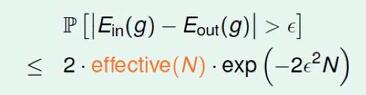
图4.8
在上述具体的示例中,不等式右边当N无穷大时趋于0,则代表学习错误的概率近似为0。
假设的有效数字(Effective Number of Hypotheses)

图4.9
先来引入dichotomies的概念。它本质上其实是2分法,例如对于一个二维平面,可以通过假设H,即直线将其中的圈和叉分开,最后所分成的所有集合组成了dichotomies H(x1,x2,…,xN)。H有可能是无限的,而dichotomies H因其总共有N个点,每个点都只有两种划分方法,所以最大的边界为2^N$。所以我们接下来用dichotomies的大小来取代H。

图4.10
为了消除dechotomies对X的依赖,我们定义成长函数mH(N)作为所有假设中dechotomies的最大值。
接下来引入shatter的定义。一数据集D被假设空间H打散(shatter),当且仅当对D的每个划分,存在H中的某假设与此划分一致(即当D的每种可能划分可由H中的某个假设来表达时,称H打散D)。注意如果一个数据集合没有被假设空间打散,那么必然存在某种划分可被定义在数据集中,但不能由假设空间表示。H的这种打散数据集合的能力是其在这些数据上定义目标函数的表示能力的度量。可以说被打散的X的子集越大,H的表示能力越强。
断点(Break Point)
成长函数中的break point其实就是第一个无法被shatter的点的数量,例如二维平面线性划分问题,当输入四个点时,理应得到16种集合,但是却是14种,于是这一类问题的break point为4。

图4.11