2 Why can machines learn?
2.1 Training vs Testing
2.1.1 Recap
两个核心问题:
- 能否保证\(E_{out}(g)≈E_{in}(g)\)?
- 能否使得\(E_{in}(g)≈0\)?

理解:
- 1.如果g≈f,则必有\(E_{out}(g)≈0\);
- 2.数据集D是在输入总体X上随机采样,并通过未知的映射模式f得到的(总体X的分布P是未知的);
- 3.只要M是有限的,且N足够大,那么Hoeffding不等式就能以PAC的方式,庇佑假设空间中每一个h都不会在D上踩雷,即以PAC的方式保证\(E_{out}(g)≈E_{in}(g)\);此时,算法A就可以自由选择想要的h作为最终的g,而不用担心选择的h不满足\(E_{out}(g)≈E_{in}(g)\);(换句话说,只要M和N达到1.4.4节的要求,就能以PAC的方式保证\(E_{out}(g)≈E_{in}(g)\))
- 4.在满足上一条情况下,如果算法A选择了某个h,使得\(E_{in}(g)≈0\),则可以获得\(E_{out}(g)≈0\);
- 5.虽然能以PAC的方式保证\(E_{out}(g)≈E_{in}(g)\),但天有不测风云,万一运气超背踩到雷,则不能保证\(E_{out}(g)≈E_{in}(g)\),所以训练之后还需要测试,让心里有个底。
大M小M的权衡如下,故当M为无穷大时,能否找到一个\(e^{2Nε^2}\)的低阶无穷大(记为\(X_H\))来代替M,就成了解决第一个核心问题的关键。
- M较小:好处是踩雷概率小;坏处是选择太少,可能无法获得\(E_{in}(g)≈0\);
- M较大:好处是选择较多;坏处是踩雷概率大。
从踩雷容忍度和踩雷概率的角度来看:

2.1.2 寻找\(X_H\)
几个概念:
- dichotomy(二分类):一个h对数据集D中N个样本的输出就称为D的一种dichotomy,即\(h(x_1,x_2,...x_n)\),一个dichotomy就是D的一个划分。很显然,对于二分类问题,任意 Hypothesis Set 对N个样本最多有\(2^N\)种dichotomy,即\(H(x_1,x_2,...x_n)≤2^N\) 。如果Hypothesis Set能将数据集D中N个点分解成\(2^N\)种dichotomies,则称该Hypothesis Set 能 shatter 该D。
- 成长函数(Growth Function):\(m_H(N)=max|H(x_1,x_2,...x_n)|\)。比如在二维线性分类中,\(m_H(N)\)分别为2(N=1)、4(N=2)、8(N=3)、14(N=4)...。注意:成长函数\(m_H(N)\)是 Hypothesis Set本身的性质,它代表了 Hypothesis Set 最多能将N个样本分成多少种 dichotomy,也就是我们所说的H最多可以归纳成几种 hypothesis(即effective number of hypotheses)。
- 对于确定的H,无论样本怎么变化,只要样本数N确定,最大的dichotomy数量(也就是成长函数的取值)就是确定的。比如对于PLA,\(m_H(3)\)就等于 8 (6和8的最大值是8)。
- 不同的Hypothesis Set有不同的\(m_H(N)\),例如:

- Break point:当N从某一点k开始,Hypothesis Set 做不出\(2^N\)种 dichotomy(即该假设空间不能shatter数据集中N个点,shatter为全部打散),这个对我们意义重大的点k就称为Hypothesis Set 的 Break Point。一旦Hypothesis Set出现Break Point点k,则原来增长极快的\(m_H(N)=2^N\),会被迅速拖住,使得当N=k+1、k+2、k+3...时,\(m_H(N)\)与\(2^N\)差距越来越大。例如在二维线性分类中,\(m_H(N)\)分别为2(N=1)、4(N=2)、8(N=3)、14(N=4)、22(N=5)...
用成长函数\(m_H(N)\)代替\(X_H\)仍然不够理想,因为不同的Hypothesis Set有不同的\(m_H(N)\),在某些情况(没有Break Point)下,\(m_H(N)\)可以一直取到上限值\(2^N\),而我们的目的是要找到一个\(e^{2Nε^2}\)的低阶无穷大,且希望\(X_H\)与Hypothesis Set细节无关。
2.2 Theory of generalization
2.2.1 Bounding function
尽管不同的Hypothesis Set有不同的\(m_H(N)\),但是可以证明,只用一个Break Point即可控制住不同的\(m_H(N)\)上限。记D中样本个数为N,Break Point为k,\(m_H(N)\)上限为B(N,k):
- 当N<k时,\(B(N,k)=2^N\)
- 当N=k时,\(B(N,k)=2^N-1\)
- 当N>k时,\(B(N,k)≤B(N-1,k-1)+B(N-1,k)\) (该情况更常见)

Bounding function(与Hypothesis Set已经无关)可总结为:

上述不等式的右边是最高阶为k-1的N多项式,也就是说成长函数\(m_H(N)\)的上界B(N,K)的上界满足多项式分布poly(N),这就是我们想要得到的结果。也就是说,如果能找到一个Hypothesis Set的break point,且是有限大的,那么就能通过Hoeffding不等式,利用增大样本数N限制住“踩雷概率”,使得预测准确率和训练准确率的差值超出误差的概率尽可能的小。

2.2.2 VC Bound
事实上并不能简单用成长函数去替换\(X_H\),在无限假设空间下训练误差和预测误差真正满足的公式长这样(第二行,证明略):

小结:
- 只要存在break point,那么其成长函数\(m_H(N)\)的上界就是N的k-1阶多项式,是\(e^{2Nε^2}\)的低阶无穷大,因此可以通过VC Bound不等式,利用增大样本数N限制住“踩雷概率”。即只要break point存在,且N足够大,那么就能保证\(E_{in}≈E_{out}\)。
- 若要成功学习,需要四个条件:1.好的D(N足够大);2.好的H(存在break point);3.好的算法A(能选出\(E_{in}\)最小的h);4.一点点运气(不要踩到雷)。
- 注意理解:VC公式中,至少存在一个h踩雷的概率被限制在一定范围。
2.3 VC dimension
核心:根据VC Bound推导结论。
2.3.1 VC dimension 定义
VC dimension定义:\(d_{VC} = k - 1\),或者说H最大能shatter的D的个数。(数据集D是否可被shatter,取决于:1.\(d_{VC}\)与N的大小关系;2.D的分布P。)
VC dimension是H本身固有的性质。

2.3.2 VC dimension of Perceptrons
若感知机的维度为d,则\(d_{VC} = d+1\)
证明方向:
- 1.证明\(d_{VC} ≥ d+1\):构造一个特殊的D,内含d+1个样本点,构成的X可逆,则对于任意一种dichotomy,都有对应的解\(w=X^{-1}y\),即D能被shatter;
- 2.证明\(d_{VC} ≤ d+1\):对于任意一个有d+2个样本点的D,由于样本点的长度为d+1(包括常数项),故该X中各样本向量必定线性相关,即存在某一个样本点可用其余向量表示,则当等式两边均乘以某一个\(W^T\)时(一个W对应一个超平面),该样本点的正负即随之而定,不存在可正可负的情况,即说明d+2个样本点无法被shatter。
2.3.3 VC dimension的意义
意义1:只要存在有限\(d_{VC}\),且N足够大,那么就能保证\(E_{in}≈E_{out}\)。(不用关心P、f、A的情况。)
意义2:\(d_{VC}\)是H能够shatter的最大个数,表征了H的表达能力。\(d_{VC}\)越大,模型的表达能力就越强,则更有能力选出更小的\(E_{in}\)。
意义3:\(d_{VC}\)越大,模型复杂度越高,踩雷概率变大,VC Bound不等式对复杂度的惩罚(Ω)就越大。即如果要维持踩雷概率δ,保证同样的泛化误差ε,则需要更多的N。(注意δ和ε的关系式)
\(d_{VC}\)是矛盾的中心,\(d_{VC}\)越大,\(E_{in}\)越小,但是\(E_{in}\)和\(E_{out}\)偏差就越大。如果我们希望获得更好的预测表现,并不能一味地追求更大的\(d_{VC}\),模型复杂度也并非越高越好,控制和选择合适的\(d_{VC}\)是机器学习算法设计非常重要的技巧。

注意:
- \(d_{VC}\)是H能够shatter的最大个数,表征了H的表达能力。\(d_{VC}\)越小,踩雷概率δ越小,但H的表达能力越弱;\(d_{VC}\)越大,H的表达能力越强,但δ越大。
- \(d_{VC}\)表征了二分型H的自由度,大致等同于可调节的独立参数。例如Positive Rays(\(d_{VC}=1\)),Positive Intervals(\(d_{VC}=2\)),感知机(\(d_{VC}=d+1\))
- 下图是关于成长函数、Bound函数、poly(N)。故由VC Bound可知,当存在break point时:\(P(踩雷)≤4(2N)^{d_{VC}}exp(-1/8Nε^2)\)

- 模型复杂度:红色石头笔记说是根号这一坨Ω,但课件上说Ω是对模型复杂度的惩罚,实际上Ω这一坨是泛化误差ε的具体表示。故暂认为模型复杂度为模型的自由度,即可调节的独立参数。

2.3.4 样本复杂度
样本复杂度:N的大小。
那么,如果选定\(d_{VC}\),样本数据D的容量N选择多少合适呢?

计算结果显示N大约是\(d_{VC}\)的10000倍。这个数值太大了,实际中往往不需要这么多的样本数量,大概只需要\(d_{VC}\)的10倍就够了。N的理论值之所以这么大是因为VC Bound 过于宽松了,我们得到的是一个比实际大得多的上界。宽松原因如下。

值得一提的是,VC Bound虽然比较宽松,但很难进一步收紧。但是,令人欣慰的一点是,VC Bound基本上对所有模型的宽松程度是基本一致的,所以,不同模型之间还是可以横向比较。从而,VC Bound宽松对机器学习的可行性还是没有太大影响。
2.4 Noise and error
- Noise 来源
- 由于人为因素,正类被误分为负类,或者负类被误分为正类;
- 同样特征的样本被模型分为不同的类;
- 样本的特征被错误记录和使用。
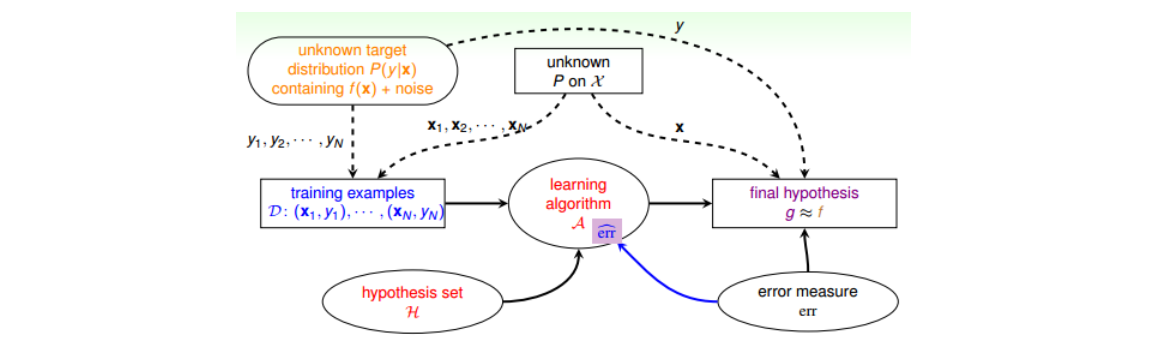
- 之前的数据集是确定的,即没有Noise,我们称之为Deterministic。现在有Noise了,也就是说在某点处不再是确定分布,而是概率分布了,即对每个(x,y)出现的概率是P(y|x)。比如在x点,有0.7的概率y=1,有0.3的概率y=0。数学上可以证明如果数据集按照P(y|x)概率分布且是iid的,那么以前证明机器可以学习的方法依然奏效。P(y|x)称之为目标分布(Target Distribution)。它实际上告诉我们最好的选择是什么,同时伴随着多少noise。

- Error measure:有0-1 err、Squared err等,Ideal Mini Target由P(y|x)和err共同决定,不同的err选出的g可能不一样。
- 实际问题中,对false accept和false reject可能选择不同的权重(犯错严重程度不一样、数据不平衡等)。