机器学习技法课程概述:
- 如何利用众多特征,并控制复杂度的问题? ——催生了SVM;
- 如何找到以及混合更有预测性的特征,以使ML表现更好? ——催生了AdaBoost;
- 如何找到/学到数据中真正的特征(而不是人为给定的特征)? ——催生DL。
1 Embedding Numerous Features: Kernel Models
1.1 Linear Support Vector Machine
概述:本节课主要介绍了线性支持向量机(Linear Support Vector Machine)。先从视觉角度出发,希望得到一个比较“胖”的分类面,即在分类正确的前提下,满足所有的点距离分类面都尽可能远。然后通过一步步推导和简化,最终把这个问题转换为标准的二次规划(QP)问题。二次规划问题可以使用Matlab等软件来进行求解,得到我们要求的w和b,确定分类面。这种方法背后的原理其实就是减少了dichotomies的种类,减少了有效的VC Dimension数量,从而让机器学习的模型具有更好的泛化能力。
1.1.1 缘起
对于数据集D线性可分的情况,我们可以使用PLA/pocket算法在平面或者超平面上把正负类分开,但符合条件的分类器通常不止一个。直觉上,我们会选择离两侧点间隔最大的分类直线,如图右侧所示。因为一般情况下,训练样本外的测量数据应该分布在训练样本附近,但与训练样本的位置有一些偏差;若要保证对未知的测量数据也能进行正确分类,最好让分类直线距离正类负类的点都有一定的距离,这样分类线就可以忍受更大的测量误差(noise),对过拟合问题就更加Robust(噪声也是造成过拟合的一个原因)。即分类线越胖越好。
故,我们的目标就是:1.分类正确,即\(y_n(w^T*x+b)>0\);2.最大化间隔(离分类线最近的点到分类线距离)。数学表达为(注:此处w包括了b,表示分类线,后续分开):

1.1.2 Standard Large-Margin Problem
注意:本课中N表示样本数量,d表示样本维度。
定义:
- 超平面关于D中样本点的函数间隔为\(\hat{\gamma}_i = y_i(w \cdot x_i + b)\);超平面(w,b)关于训练数据集D的函数间隔为超平面关于D中各样本点的函数间隔最小值;
- 超平面关于D中样本点的几何间隔为\(\gamma_i = \dfrac{y_i(w \cdot x_i + b)}{\Vert w \Vert}\);超平面(w,b)关于训练数据集D的几何间隔为超平面关于D中各样本点的几何间隔最小值;
要让margin最大,即让离分类线最近的点到分类线距离最大。由于点到超平面的函数间隔可缩放而保持超平面不变,故问题中的距离采用几何间隔,规定超平面关于D的函数间隔为1。故原问题转化为:

经过等价变换后,得到目标及条件为:

问题求解:
这是一个典型的二次规划问题,即Quadratic Programming(QP)。因为SVM的目标是关于w的二次函数,条件是关于w和b的一次函数,所以,它的求解过程还是比较容易的,可以使用一些软件(例如Matlab,Python里面也有)自带的二次规划的库函数来求解(将对应的二次规划参数Q,p,A,c丢进去,库函数将求解好的u吐出来)。下图给出SVM与标准二次规划问题的参数对应关系:

故线性SVM算法可以总结为三步:
- 将b、w包装成向量u,计算对应的二次规划参数Q,p,A,c;
- 根据二次规划库函数,计算u(即b,w);
- 将b和w代入\(g_{SVM}\),得到最佳分类面。
这种方法称为Linear Hard-Margin SVM Algorithm。如果是非线性的,例如包含x的高阶项,那么可以使用我们之前在《机器学习基石》课程中介绍的特征转换的方法,先作\(z_n=\Phi(x_n)\)的特征变换,从非线性的x域映射到线性的z域空间,再利用Linear Hard-Margin SVM Algorithm求解即可。
Support Vector Machine(SVM)这个名字从何而来?为什么把这种分类面解法称为支持向量机呢?这是因为分类面仅仅由分类面的两边距离它最近的几个点决定的,其它点对分类面没有影响。决定分类面的几个点称之为支持向量(Support Vector),好比这些点“支撑”着分类面。而利用Support Vector得到最佳分类面的方法,称之为支持向量机(Support Vector Machine)。
1.1.3 Reasons behind Large-Margin Hyperplane
角度1:类似Regularization思想
SVM的这种思想其实与我们之前介绍的机器学习非常重要的正则化regularization思想很类似。regularization的目标是将\(E_{in}\)最小化,条件是\(w^Tw\leq C\);SVM的目标是\(w^Tw\)最小化,条件是\(y_n(w^Tx_n+b)\geq1\),即保证了\(E_{in}=0\)。即regularization与SVM的目标和限制条件分别对调了,但考虑的内容是类似的,效果也是相近的。SVM也可以说是一种weight-decay regularization,限制条件是\(E_{in}=0\)。

角度2:Large-Margin降低有效VC维度
Large-Margin会限制Dichotomies的个数。这从视觉上也很好理解,假如一条分类面越“胖”,即对应Large-Margin,那么它可以shatter的点的个数就可能越少。Dichotomies越少,那么复杂度就越低,即有效的VC Dimension就越小,得到\(E_{out}\approx E_{in}\),泛化能力增强。

1.2 Dual Support Vector Machine
这节课主要介绍了SVM的另一种形式:Dual SVM。这样做的出发点是为了移除计算过程对\(\tilde d\)的依赖。Dual SVM解决问题的过程是,利用拉格朗日对偶性,将Primal Hard-Margin SVM问题转化为Dual Hard_Margin SVM问题,并通过QP工具包获得拉格朗日因子\(\alpha\),然后通过KKT条件计算出\(w^*、b^*\)。
1.2.1 Motivation of Dual SVM
对于非线性SVM,我们通常可以使用非线性变换将变量从x域转换到z域中。然后,在z域中,根据上一节课的内容,使用线性SVM解决问题即可。使用特征转换,目的是让模型具有更强的表达能力,减小\(E_{in}\);而SVM的Large-Margin减少了有效的VC Dimension,可在一定程度上抑制过拟合。所以说,非线性SVM是把这两者目的结合起来,平衡这两者的关系。但是,在特征转换后,设z域中的维度为\(\tilde d +1\)(仅仅二次转换就会使维度大大增加),如果模型越复杂,则\(\tilde d +1\)越大,相应求解这个QP问题也变得很困难。一种方法就是使SVM的求解过程不依赖\(\tilde d\),这就是我们本节课所要讨论的主要内容。

1.2.2 Lagrange Dual SVM
上一节课所讲的Original SVM二次规划问题的变量个数是\(\tilde d +1\),有N个限制条件;而本节课,我们把问题转化为对偶问题(’Equivalent’ SVM),同样是二次规划,只不过变量个数变成N个,有N+1个限制条件。这种对偶SVM的好处就是问题只跟N有关,与\(\tilde d\)无关,这样就解决了上文提到的当\(\tilde d\)过大时难以求解的情况。
**目标:**通过拉格朗日对偶性,将SVM原始问题转化为对偶问题,通过求解对偶问题得到原始问题的最优解。
步骤:
第一步:通过构造拉格朗日函数,将带约束条件的原始问题转化成不带约束条件的最大最小值问题(拉格朗日因子\(\alpha_n \geq 0\),for all n);

理解:首先,由于转换后线性可分,故最优解必定存在。其次,由于先对拉格朗日函数求最大化,故所有不符合约束条件\((1−y_n(w^T z_n+b)) \leq 0\)的\(w\)和\(b\)均会导致无解,即最优解\(w^*\)和\(b^*\)必定符合约束条件。最后,为了最大化拉格朗日函数,最优解和\(\alpha_n\)必定满足各拉格朗日项均为0,使得该问题等价于最小化\(1/2 w^T w\),即等价于原问题。
第二步:将该最大最小值问题转化为对偶SVM问题;
现在,我们已经将SVM问题转化为与拉格朗日因子\(\alpha_n\)有关的最大最小值形式。已知\(\alpha_n\geq0\),那么对于任何固定的\(\alpha'\)(向量),且\(\alpha_n’\geq0\),一定有如下不等式成立:

对上述不等式右边取最大值,不等式同样成立:

如此,即将原始问题转化为拉格朗日对偶问题。已知\(\geq\)是一种弱对偶关系,在二次规划QP问题中,如果满足三个条件(函数是凸的(convex primal),函数有解(feasible primal),条件是线性的(linear constraints)),上述不等式关系就变成强对偶关系,\(\geq\)变成\(=\),即一定存在满足条件的解\((b,w,\alpha)\),使等式左边和右边都成立,SVM的解就转化为右边的形式。
接下来简化右边对偶问题,通过对b和w的求导,将条件提取出来。

最终,SVM最佳化形式转化为只与\(\alpha_n\)有关:

其中,满足最佳化的条件称之为Karush-Kuhn-Tucker(KKT),即为上述不等式关系变成强对偶关系的充要条件:

第三步:求解对偶问题;
将上述简化版的SVM对偶问题变形得:

则根据上一节课讲的QP解法,找到Q,p,A,c对应的值,用软件工具包进行求解\(\alpha\)。(约束条件里为啥没有KKT里面第四个?答:w和b变量都是随着\(\alpha\)而变的,所以这个式子对\(\alpha\)没有约束力。)

注意:
- \(\Vert \sum\limits_{n=1}^N z_n \Vert^2 = (\sum\limits_{n=1}^N z_n) \cdot (\sum\limits_{m=1}^N z_m) = \sum\limits_{n=1}^N \sum\limits_{m=1}^N (z_n \cdot z_m)\)的推导;
- \(\sum\limits_{n=1}^N \sum\limits_{m=1}^N \alpha_n \alpha_m y_n y_m(z_n \cdot z_m) = \alpha^T Q \alpha\)中,\(q_{n,m} = y_n y_m(z_n \cdot z_m)\)的推导。
- 现在QP工具包通常会提供等号的约束条件接口,故无需拆分。
- 由于\(q_{n,m}\)大部分值是非零的,称为dense,当N很大的时候,例如N=30000,那么对应的\(Q_D\)的计算量将会很大,存储空间也很大(大于3GB)。所以一般情况下,对dual SVM问题的矩阵\(Q_D\),需要使用后续的核技巧。
第四步:根据求得的\(\alpha\)求解\(w^*、b^*\)。
根据求得的\(\alpha\),以及KKT条件,即可求得\(w^*、b^*\)。首先利用\(w = \sum\limits_{n=1}^N \alpha_n y_n z_n\)求出\(w^*\);然后利用\(\alpha_n(1−y_n(w^T z_n+b)) = 0\),任取一个\(\alpha_n > 0\)的点,得到\(1−y_n(w^T z_n+b) = 0\),即可得\(b = y_n - w^T z_n\)。
1.2.3 Messages behind Dual SVM
上一节课中把位于分类线边界上的点称为support vector candidates。本节课前面介绍了\(\alpha_n>0\)的点一定落在分类线边界上(\(1−y_n(w^T z_n+b) = 0\)),这些点称之为SV(注意没有candidates)。也就是说分类线上的点不一定都是SV,但是满足\(\alpha_n>0\)的点,一定是SV。

\(\alpha_n>0\)的点称为SV,w和b仅由support vectors(SVs)决定,简化了计算量。即样本点可以分成两类:一类是SV,通过SVs可以求得fattest hyperplane;另一类不是SV,对求fattest hyperplane没有影响。

另一方面,比较一下SVM和PLA的w公式可以发现,二者在形式上是相似的。\(w_{SVM}\)由fattest hyperplane边界上所有的SV决定,\(w_{PLA}\)由所有当前分类错误的点决定。\(w_{SVM}\)和\(w_{PLA}\)都是原始数据点\(y_n z_n\)的线性组合形式,这一结论对基于GD/SGD的LinReg/LogReg也成立(b=0时), 称它们为“represented by data”。

1.2.4 小结
本节课和上节课主要介绍了两种形式的SVM,一种是Primal Hard-Margin SVM,另一种是Dual Hard-Margin SVM。Primal Hard-Margin SVM有\(\tilde d+1\)个参数,有N个限制条件。当\(\tilde d+1\)很大时,求解困难。而Dual Hard-Margin SVM有N个参数,有N+1个限制条件。当数据量N很大时,也同样会增大计算难度。两种形式都能得到w和b,求得fattest hyperplane。通常情况下,如果N不是很大,一般使用Dual SVM来解决问题。

但是需注意,这里Dual SVM并未真的消除了对\(\tilde d\)的依赖。因为在计算\(q_{n,m} = y_n y_m(z_n \cdot z_m)\)的过程中(注意为点乘),z向量引入了\(\tilde d\),实际上复杂度已隐藏在计算过程中了。故需后续的核技巧来解决这一问题。

1.3 Kernel Support Vector Machine
上节课中提到dual SVM的计算过程其实仍然没有摆脱高维度\(\tilde d\),这节课主要内容就是利用核技巧摆脱\(\tilde d\)。
1.3.1 Kernel Trick
上节课推导的dual SVM如下形式。其中,计算\(q_{n,m} = y_n y_m(z_n \cdot z_m)\)时涉及到了\(\tilde d\),这一步是计算的瓶颈所在。

已知z是由x经过特征转换而来,故\(z_n \cdot z_m = \phi(x_n) \cdot \phi(x_m)\)。这个过程涉及到两个环节,一个是向高维转换,一个是在高维空间中做内积。核技巧的核心在于,不走这两个步骤,而是\(x_n和x_m\)先在低维空间上做内积之后,直接通过一个函数求得结果,即走捷径。
先看一个简单例子,对于二阶多项式转换,\(\phi_2(x_n) \cdot \phi_2(x_m)\)复杂度由\(O(d^2)\)降低至\(O(d)\)。

通常把合并特征转换和计算内积这两个步骤的操作叫做Kernel Function,用大写字母K表示。例如刚刚讲的二阶多项式例子,它的kernel function为:
有了核函数之后,就可以在不涉及\(\tilde d\)的情况下,求出b和最优分类面\(g_{SVM}\)(注意,w要涉及\(\tilde d\),故无法求出)。整个计算过程中都没有在z空间作内积,即与z无关。我们把这个过程称为kernel trick,也就是把特征转换和计算内积两个步骤结合起来,用kernel function来避免计算过程中受\(\tilde d\)的影响,从而提高运算速度。

总结一下,Kernel SVM算法过程和复杂度。

1.3.2 Polynomial Kernel
刚刚通过一个特殊的二次多项式导出了相对应的kernel,其实二次多项式的kernel形式是多种的。比如下图三种二次kernel,从某种角度来说是一样的,因为都是二次转换,对应到同一个z空间。但是,它们系数不同,内积就会有差异,那么就代表有不同的距离,最终可能会得到不同的SVM margin和SVM分界线。通常情况下,第三种(绿色标记)简单一些,更加常用。

归纳一下,引入\(\zeta\geq 0\)和\(\gamma>0\),对于Q次多项式一般的kernel形式可表示如下。当多项式阶数Q=1时,那么对应的kernel就是线性的,即本系列课程第一节课所介绍的内容。

1.3.3 Gaussian Kernel
刚刚介绍的Q阶多项式kernel的阶数是有限的,即特征转换的\(\tilde d\)是有限的。而高斯kernel能将特征转换扩展至无限维空间。
举个例子,假设原空间维度为1,只有一个特征x,我们构造一个kernel function为高斯函数:
构造的过程正好与二次多项式kernel的相反,利用反推法,先将上式分解并做泰勒展开:

由此我们得到了\(\Phi(x)\),\(\Phi(x)\)是无限多维的,它就可以当成特征转换的函数,且\(\tilde d\)是无限的。这种\(\Phi(x)\)得到的核函数即为Gaussian kernel。更一般地,对于原空间不止一维的情况(d>1),引入缩放因子\(\gamma>0\),它对应的Gaussian kernel表达式为:
Gaussian kernel能将特征转换扩展到无限维,并使用有限个SV数量的高斯函数构造出矩\(g_{SVM}\)。

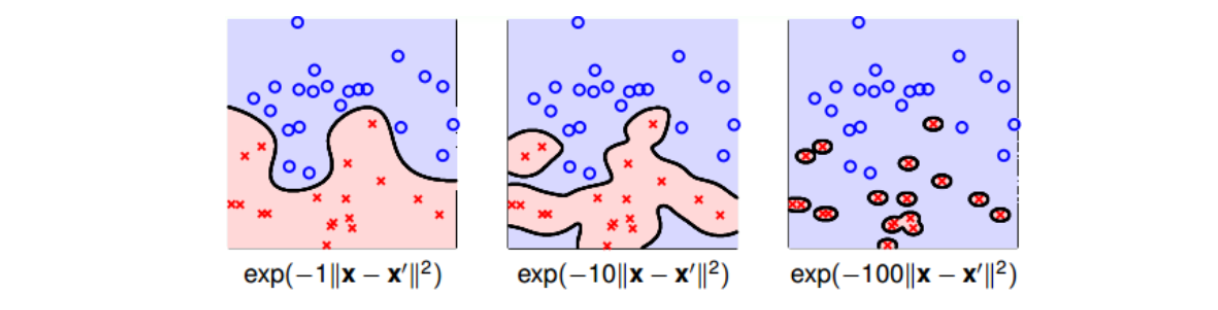
值得注意的是,缩放因子\(\gamma\)取值不同,会得到不同的高斯核函数,hyperplanes不同,分类效果也有很大的差异。(对应到Ng课中,高斯函数为\(K(x, x') = e^{-\frac{\Vert x-x'\Vert^2}{2\sigma^2}}\),其中\(\sigma\)表示高斯核函数的方差,\(\gamma\)越大,对拟合越敏感。)举个例子,\(\gamma\)分别取1, 10, 100时对应的分类效果如下:
1.3.4 Comparison of Kernels
1). Linear Kernel
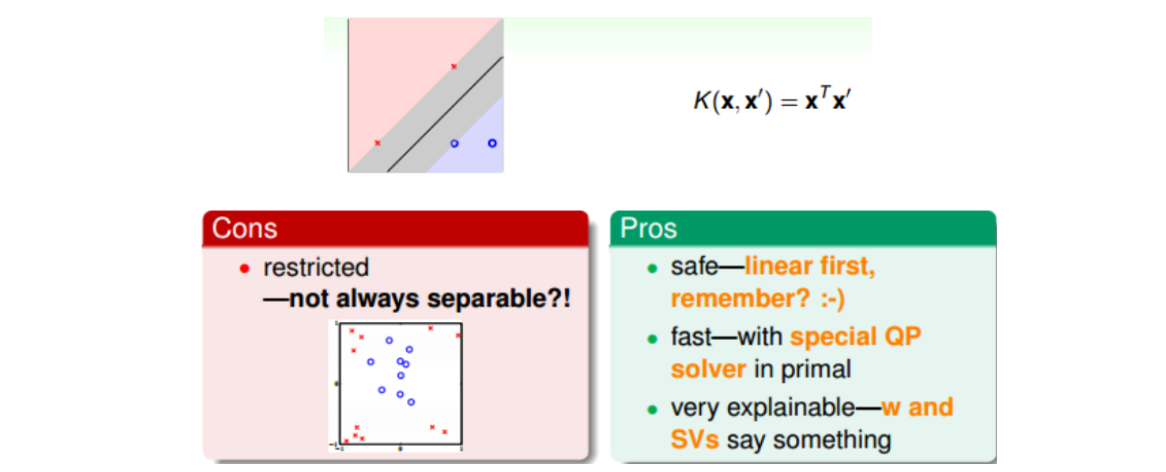
Linear Kernel是最简单最基本的核,平面上对应一条直线,三维空间里对应一个平面。Linear Kernel可以使用Primal SVM中QP,或者Dual SVM中QP直接计算得到。
2). Polynomial Kernel
Polynomial Kernel的hyperplanes是由多项式曲线构成,优点是阶数Q可以灵活设置,相比linear kernel限制更少,更贴近实际样本分布;缺点是当Q很大时,K的数值范围波动很大,而且参数个数较多,难以选择合适的值。

3). Gaussian Kernel
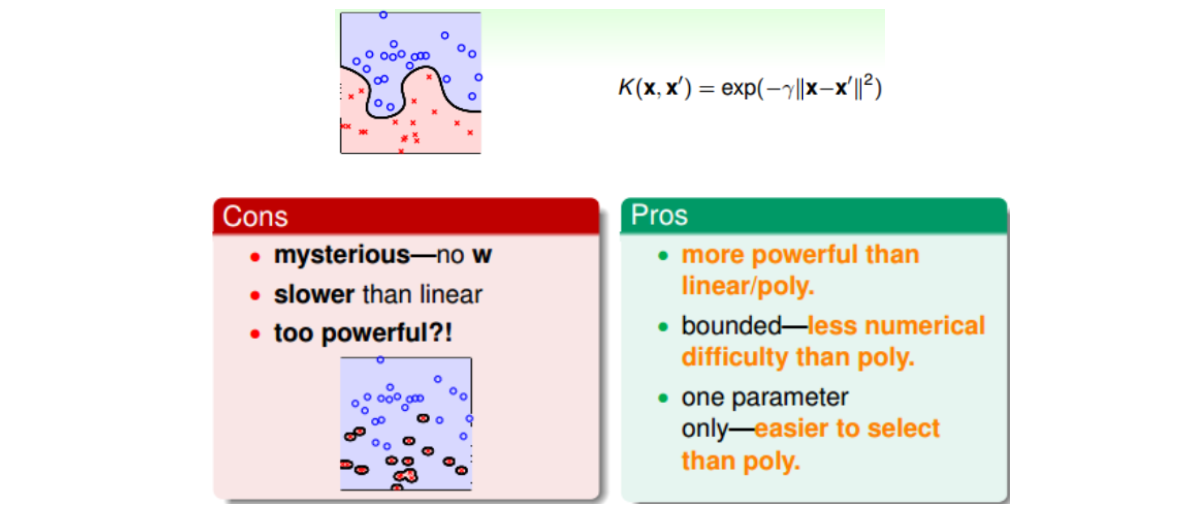
4). 其他形式的核
实际上kernel代表的是两笔资料\(x和x’\)特征变换后的相似性即内积。但是不能说任何计算相似性的函数都可以是kernel。有效的kernel还需满足两个条件:K是对称的;K是半正定的。这两个条件为Kernel有效的充要条件,这称为Mercer定理。事实上,构造一个有效的kernel是比较困难的。

1.4 Soft-Margin Support Vector Machine
上节课介绍的Kernel SVM不仅能解决简单的线性分类问题,也可以求解非常复杂甚至是无限多维的分类问题,关键在于核函数的选择。但是,这些方法都是Hard-Margin SVM,即必须将所有的样本都分类正确才行。这往往需要更多更复杂的特征转换,甚至造成过拟合。本节介绍的Soft-Margin SVM允许有noise存在。这种做法很大程度上不会使模型过于复杂,避免过拟合,而且分类效果令人满意。
1.4.1 Motivation and Primal Problem
上节课中提到SVM可能会造成过拟合,原因是,由于约束条件坚持要将所有的样本都分类正确,连noise也不放弃,导致转换的维度过大,使得模型过于复杂。

为了避免过拟合,可以允许有分类错误的点,即把某些点当作是noise,放弃这些noise点,但是尽量让这些noise个数越少越好。回顾一下我们在机器学习基石笔记中介绍的pocket算法,pocket的思想不是将所有点完全分开,而是找到一条分类线能让分类错误的点最少。为了引入允许犯错误的点,我们将Hard-Margin SVM的目标和条件做一些结合和修正。

这个修正后的优化目标存在两个不足的地方。首先,最小化目标中第二项是非线性的,不满足QP的条件,所以无法使用dual或者kernel SVM来计算。然后,对于犯错误的点,上式的条件和目标没有区分small error和large error。这种分类效果是不完美的。
为了改正这些不足,我们引入了新的参数\(\xi_n\)来表示每个点犯错误的程度值,\(\xi_n\geq0\)。通过使用error值的大小代替是否有error,让问题变得易于求解,满足QP形式要求。

其中,\(\xi_n\)表示每个点犯错误的程度,\(\xi_n=0\)表示没有错误,\(\xi_n\)越大,表示错误越大,即点距离胖边界(负的)越大。参数C表示尽可能选择宽边界和尽可能不要犯错两者之间的权衡,因为边界宽了,往往犯错误的点会增加。large C表示希望得到更少的分类错误,即不惜选择窄边界也要尽可能把更多点正确分类;small C表示希望得到更宽的边界,即不惜增加错误点个数也要选择更宽的分类边界。与之对应的QP问题中,总共参数个数为\(\tilde d+1+N\),总条件个数为2N。
1.4.2 Dual Problem
有了Soft-Margin的优化目标之后,按照之前方式求出Soft-Margin SVM的对偶形式,从而让QP计算更加简单,并便于引入kernel算法。过程如下。

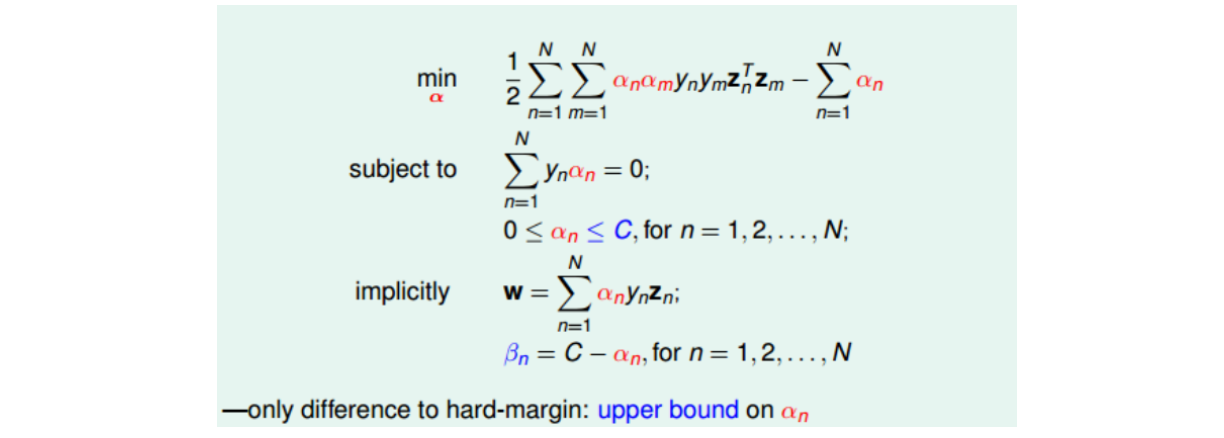
此时KKT条件为:
- \(y_n(w^T z_n + b) \geq 1-\xi_n\),\(\xi_n \geq 0\);
- \(0 \leq \alpha_n \leq C\);
- \(w=\sum\limits_{n=1}^N \alpha_n y_n z_n, \sum\limits_{n=1}^N \alpha_n y_n = 0, \alpha_n + \beta_n = C\);
- \(\alpha_n(1-\xi_n - y_n(w^T z_n + b))=0, \beta_n \xi_n=0\).
1.4.3 Messages behind Soft-Margin SVM
1).求解过程
推导完Soft-Margin SVM Dual的简化形式后,就可以利用QP,找到Q,p,A,c对应的值,用软件工具包得到\(\alpha_n\)的值,过程与Hard-Margin SVM Dual的过程是相同的(除了求b有些小区别)。

求b这一步时,由于在Soft-Margin SVM Dual中,相应的complementary slackness条件有两个:
故仅有SV(\(\alpha_n>0\)的点)还不够,还需要\(0<\alpha_n<C\)(这种点称为free SV)。任取满足这个条件的某个\(\alpha_n\),计算得到\(b = y_s - \sum\limits_{SV}\alpha_n y_n K(x_n, x_s)\)。一般情况下,至少存在一组SV使\(\alpha_s < C\),但如果运气特背,出现了没有free SV的情况,那么b通常会由许多不等式条件限制取值范围,值是不确定的,只要能找到其中满足KKT条件的任意一个b值就可以了。

2).C的意义
C值反映了margin和分类正确的一个权衡。C越小,越倾向于得到粗的margin,宁可增加分类错误的点;C越大,越倾向于得到高的分类正确率,宁可margin很细。当C值很大的时候,虽然分类正确率提高,但很可能把noise也进行了处理,从而可能造成过拟合。

3).\(\alpha_n\)取值意义
已知\(0\leq\alpha_n\leq C\)满足两个complementary slackness条件,故:
- 若\(\alpha_n = 0\),则\(\xi_n = 0\),对应的点不是SV,在margin之外(或者在margin上),且均分类正确。
- 若\(0<\alpha_n<C\),则\(\xi_n = 0\),且\(y_n(w^T z_n + b) = 1\),对应的点在margin上。这些点称为free SV,确定了b的值。
- 若\(\alpha_n = C\),则\(\xi_n = 1 - y_n(w^T z_n + b)\),\(\xi_n\)大小表示该点偏离margin的程度,只有当其等于0时,该点落在margin上。所以这种情况对应的点在margin之内负方向(或者在margin上),有分类正确也有分类错误的。这些点称为bounded SV。
所以在Soft-Margin SVM Dual中,根据\(\alpha_n\)的取值,就可以推断数据点在空间的分布情况。

1.4.4 Model Selection
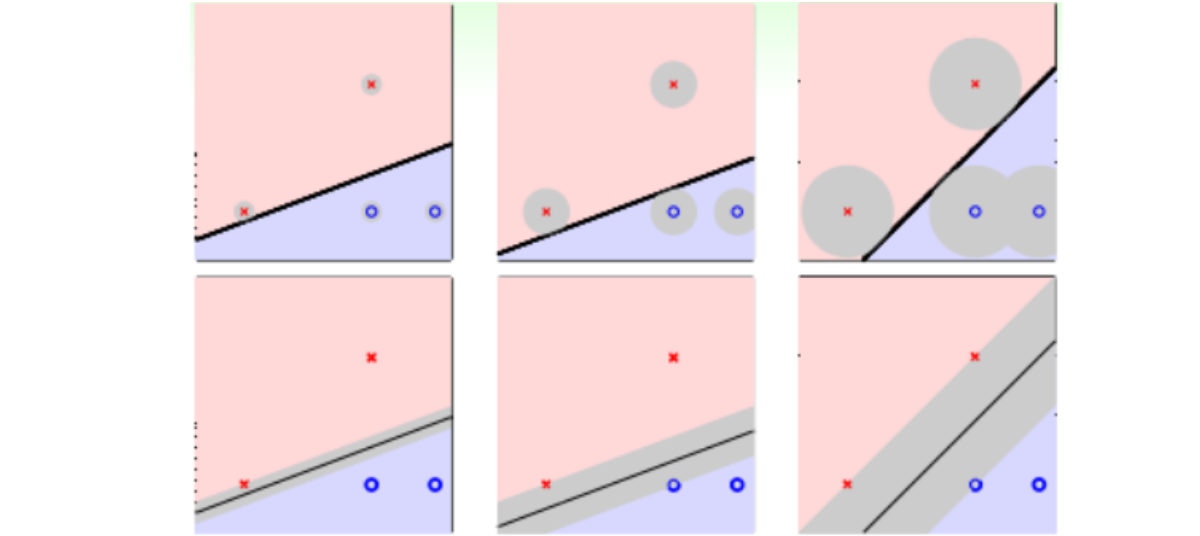
在Soft-Margin SVM Dual中,kernel的选择、C等参数的选择都非常重要,直接影响分类效果。例如,对于Gaussian SVM,不同的参数\((C,\gamma)\),会得到不同的margin,如下图所示。横坐标是C逐渐增大的情况,纵坐标是\(\gamma\)逐渐增大的情况。一般做法是利用KFold cross validation,选取不同的离散的\((C,\gamma)\)值进行组合,得到最小的\(E_{cv}(C,\gamma)\),其对应的模型即为最佳模型。

另外,K-Fold cross validation的一种极限就是Leave-One-Out CV,也就是验证集只有一个样本。对于SVM问题,它的验证集Error满足:\(E_{loocv} \leq \frac{SV}{N}\)。
SV的数量在SVM模型选择中也是很重要的。一般来说,SV越多,表示模型可能越复杂,越有可能会造成过拟合。所以,通常选择SV数量较少的模型,然后在剩下的模型中使用cross-validation,比较选择最佳模型。
1.5 Kernel Logistic Regression
本节课将把Soft-Margin SVM和之前介绍的Logistic Regression联系起来,研究如何使用kernel技巧来解决更多的问题。
注:第五课和第六课主要讲下大致概念。
1.5.1 Soft-Margin SVM as Regularized Model
Soft-Margin SVM损失函数可以转换成非约束形式,如下:

对比可以看出,Soft-Margin SVM实际上和L2正则化形式相同,都是约束一个,最小化另一个,只不过约束对象和最小化对象互换,但效果是一致的,Large-Margin等同于Regularization,都起到了防止过拟合的作用。

1.5.2 SVM versus Logistic Regression
SVM和LogReg的err对比如下图,\(\hat{err}_{SVM}\)通常称为hinge error measure。因为二者的这种相似性,SVM看成是L2-regularized logistic regression。

1.5.3 SVM for Soft Binary Classification
不同于之前SVM用于硬分类,本节将SVM的结果应用在Soft Binary Classification中,得到是正类的概率值(软分类)。
probabilistic SVM算法过程如下图:

首先利用SVM的解\((b_{svm},w_{svm})\)来构造模型,放缩因子A和平移因子B是待定系数。然后再用通用的logistic regression优化算法,通过迭代优化,得到最终的A和B。一般来说,如果\((b_{svm},w_{svm})\)较为合理的话,满足A>0且\(B\approx0\)。这种soft binary classifier方法得到的结果跟直接使用SVM classifier得到的结果可能不一样,这是因为我们引入了系数A和B。一般来说,soft binary classifier效果更好。
1.5.4 Kernel Logistic Regression(KLR)
已知一个理论,对于对于L2-regularized linear model,如果它的最小化问题形式为如下的话,那么最优解\(w^*\)就可以表示成\(z_n\)的线性组合。

据此,就可以把kernel应用在L2-regularized logistic regression上。方法是直接将\(z_n\)的线性组合表示的\(w^*\)代入到L2-regularized logistic regression最小化问题中,凑出kernel的形式即可。

我们把这种问题称为kernel logistic regression,即引入kernel,将求w的问题转换为求\(\beta_n\)的问题。但值得一提的是,KLR中的\(\beta_n\)通常都是非零值,故此方法较少用。
1.6 Support Vector Regression
本节课将讨论如何将SVM的kernel技巧应用到regression问题上。
1.6.1 Kernel Ridge Regression
根据上节课介绍的Representer Theorem,对于任何包含正则项的L2-regularized linear model,它的最佳化解w都可以写成是z的线性组合形式,因此,也就能引入kernel技巧,将模型kernelized化。所以,将\(w^*\)代入下图中ridge regression优化目标,即可凑出kernel形式。(注意:linear regression和ridge regression区别,后者是正则化的linear regression。)

优缺点的比较:对于linear ridge regression来说,它是线性模型,只能拟合直线;其次,它的训练复杂度是\(O(d^3+d^2N)\),预测的复杂度是\(O(d)\)。而对于kernel ridge regression来说,它转换到z空间,使用kernel技巧,得到的是非线性模型,所以更加灵活;其次,它的训练复杂度是\(O(N^3)\),预测的复杂度是\(O(N)\),均只与N有关。但实际上,由于后者预测复杂度过高,通常不用。

1.6.2 Support Vector Regression(SVR)
SVR是使用SVM来拟合曲线,做回归分析。与SVM是使用一个条带来进行分类一样,SVR也是使用一个条带来拟合数据。这个条带的宽度可以自己设置,利用参数\(\epsilon\)来控制。在SVM模型中边界上的点以及两条边界内部违反margin的点被当做支持向量,并且在后续的预测中起作用;在SVR模型中边界上的点以及两条边界以外的点被当做支持向量,在预测中起作用。

在SVR对偶形式中,可以使用kernel,即可以对非线性曲线拟合;且可以得到SVR的sparse解。
1.6.3 Summary of Kernel Models
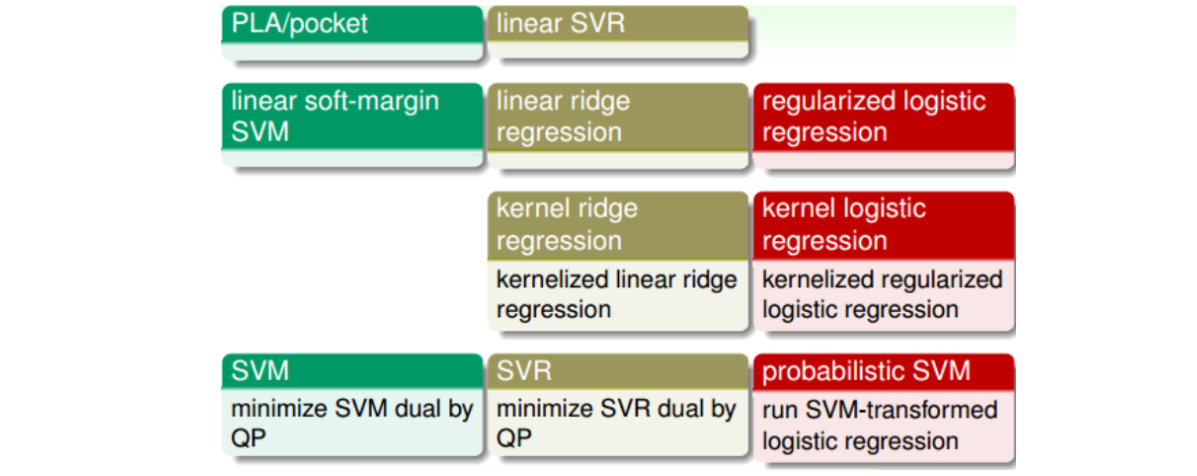
注意:第一行和第三行通常不用,前者因为表现不好,后者因为解是dense的,预测开销大。第二第四行常用,可以使用台大开发的工具包Liblinear和Libsvm。通常来说,这些模型中SVR和probabilistic SVM最为常用。