问题引入
我们先来看这样一道题:
现在有一个长度为n的数列a,我们要对数列进行m次操作,操作分为两种,对其中第k个元素进行修改,或者是计算出数列中一个区间[l,r]中所有元素的和
很容易想到用前缀和的思想,即用一个sum数组,sum[i]表示第1个元素到第i个元素的和,那么此时要求区间[l,r]中所有元素的值就可以写为sum[r]-sum[l-1]
但如果数据范围太大,岂不是就会超时了吗?所以我们就要引入一个新的数据结构——树状数组
树状数组
WHAT
树状数组(Binary Indexed Tree(B.I.T), Fenwick Tree)是一个查询和修改复杂度都为log(n)的数据结构。主要用于查询任意两位之间的所有元素之和,但是每次只能修改一个元素的值;经过简单修改可以在log(n)的复杂度下进行范围修改,但是这时只能查询其中一个元素的值(如果加入多个辅助数组则可以实现区间修改与区间查询)。
这里只介绍对树状数组的单点修改和查询操作
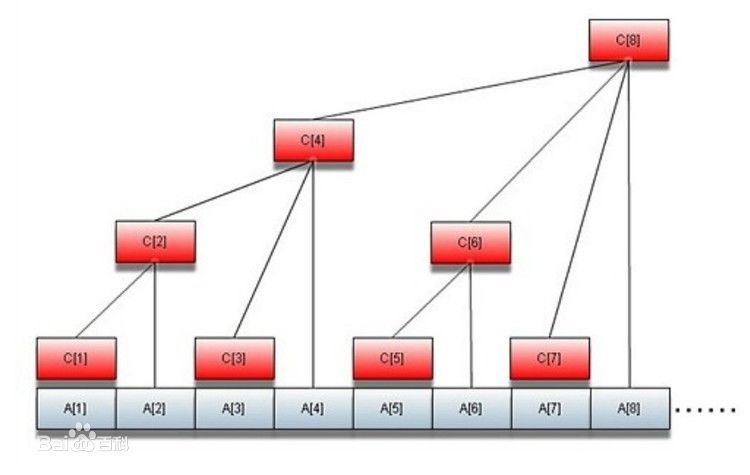
我们先用一个图来了解树状数组:
这个题很直观的展现了一个树状数组,在上图C数组中,C[i]表示以C[i]为根节点的树中所有子叶节点的和,此时树状数组的好处就充分的体现出来了
假设有一个长度为8的数列A(如上图),如果此时我们要修改A[1],如果用B数组来用普通的方法保存前缀和,那么我们总共要对B数组进行8次修改,但对树状数组C,我们只需要修改4次
现在的关键就是如何构造树状数组
HOW
lowbit
相信大家都能发现,构造树状数组的关键就是找出这个点有多少个子叶节点,此时我们需要引入lowbit
那么什么是lowbit呢?
lowbit(i)的意思是将 i 转化成二进制数之后,只保留最低位的1及其后面的0,截断前面的内容,然后再转成十进制数
可能现在不是太好理解,我们就先来看C[4],那么4的二进制数为0100,那么根据上面所说的方法,4的lowbit就为4,而根据上图可以得出,C[4]的父亲是C[8],我们可以惊奇的发现4+4=8,也就是说4加上自己的lowbit就是自己的父亲,当然4只是一个例子,大家可以再去多验证几个,这里就不多说了,我们直接来看lowbit的实现
对于lowbit这种神奇的东西,我们有两种可以求得的方法:
1、lowbit(x) = x - (x & (x - 1) )
那么我们来解释一下这个求法:
我们假设x的二进制数为A1B(此时的1就是从低位开始的最后一个1)
x - 1的二进制数就是A0C(熟悉为运算的应该都能看出,C是和B长度相同的1)
x & (x - 1)就是A1B & A0C,可以得出为A0B
x - (x & (x - 1))的二进制就是A1B - A0B,等于D0E(D是和A长度相同的0,E是和B长度相同的0)
inline int lowbit(int x){
return x - (x & (x - 1));
}2、lowbit(x) = x & -x
这个方法比较的简单,也比较好记,但因为本人能力有限,无法给各位一个严密的推理证明
inline int lowbit(int x){
return x & -x;
}update
update就是充分利用了lowbit,可以对树状数组进行更新,也就是说,如果在原来的数组中,第i号元素加上了一个数x,我们就可以用lowbit来对树状数组进行更新
因为我们已经知道第i号元素被修改了,那么第i号元素的父亲也会被修改,也就是说第i + lowbit(i)号元素也会被修改,我们就直接用一个循环修改即可
inline void update(int x, int y){
for(reg int i = x;i <= n;i += lowbit(i))
bit[i] += y;
}sum
这就是树状数组应用的体现了,即利用树状数组来求前缀和,如果我们要求第i号位的前缀和,就意味着我们除了要加上第i号元素之外,还要加上第i - lowbit(i)号元素,就可以用一个循环来解决
inline int sum(int x){
int tot = 0;
for(reg int i = x;i >= 1;i -= lowbit(i))
tot += bit[i];
return tot;
}总结
那么此时再来解决最开始的那个问题就很简单了,我们只需要对树状数组进行一个初始化,然后再用sum函数求区间元素和就可以了
#include<cstdio>
#include<cstring>
#define reg register
#define M 10005
int n, l, r;
int a[M], bit[M];
inline void read(int &x) {
x = 0; int f = 1; char s = getchar();
while(s < '0' || s > '9') {if(s == '-') f = -1; s = getchar();}
while(s >= '0' && s <= '9') {x = (x << 3) + (x << 1) + s - 48; s = getchar();}
x *= f;
}
inline void wri(int x) {
if(x < 0) {x = -x; putchar('-');}
if(x / 10) wri(x / 10);
putchar(x % 10 + 48);
}
inline void write(int x, char s) {
wri(x);
putchar(s);
}
inline int lowbit(int x) {
return x & -x;
}
inline void update(int k, int x) {
for(reg int i = k;i <= n;i += lowbit(i))
bit[i] += x;
}
inline int sum(int x) {
int tot = 0;
for(reg int i = x;i >= 1;i -= lowbit(i))
tot += bit[i];
return tot;
}
int main() {
read(n);
for(reg int i = 1;i <= n;i ++) {
read(a[i]);
update(i, a[i]);
}
read(l), read(r);
write(sum(r) - sum(l - 1), '\n');
return 0;
}
如果想了解更多树状数组的应用,可以看我更新的题解