一、线性代数基本知识：
1、线性：
数乘运算与加法运算 呈现 线性。
2、
二、向量：
1、向量的表示方法：
其中的 i、j、k是坐标轴方向的单位向量。
2、向量的模：
用坐标计算的方法：
3、向量的运算：
（1）向量的加法减法：
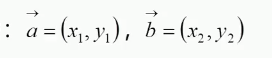
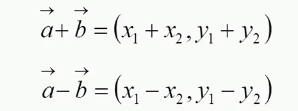
（2）向量的数乘：
拉格朗日乘数法的 基础 公式。
（3）向量的数量积（点积、内积）：
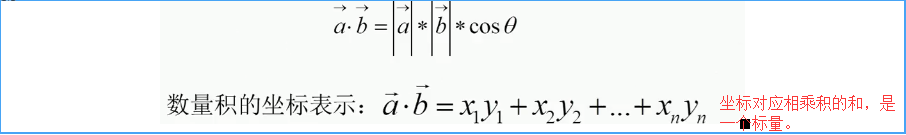
（4）向量的的向量积（外积、叉积）：
（5）正交向量：
三、矩阵基本知识：
- 理解：矩阵是一个向量组，由许多 行向量 和 纵向量 组成。
- 矩阵方程求解 用增广矩阵初等变换化为 E 。齐次/非齐次方程组 的解用 初等变化 化为 行最简阶梯型。
- 初步认为由多元一次方程组的系数组成（区别于矩阵初等变换求解矩阵方程）。矩阵是一种线性变换，可以将一些向量转化为另一种向量。
2、矩阵的直观感受：
3、矩阵与向量：
理解：A（m*n）每一行 或者 每一列 都属于 向量。
四、矩阵的分类：
1、相等矩阵：
①矩阵的形状相同（行数的列数）
②对应元素相同。
2、同形矩阵：
矩阵的形状相同。
3、方阵：
只有方阵才具有对角线。
矩阵A中 m = n，称之为方阵。
4、负矩阵、上三角矩阵、下三角矩阵：
5、对角矩阵：是方阵
1、对角矩阵的展示：可以用 上尖角 符号表示，如下：
2、对角矩阵的迹： trA
7、单位矩阵：常常用 E或I 来表示。它是一个方阵。
特性：A * E = A （A的列 = E 的行数）任何 矩阵 * 单位矩阵都是它本身。
8、零矩阵：
记号用 0 来表示。
9、对称矩阵：方阵
注意：对称矩阵一定是方阵（只有方阵才有对角线）。
五、矩阵的运算：
1、矩阵的加减：
前提：两个矩阵必须是同形矩阵。
矩阵加减具有交换律，矩阵矩阵相乘没有交换律。
计算结果：元素级运算。
2、矩阵的数乘：
计算结果：元素级运算。这里要区别与行列式的数乘。
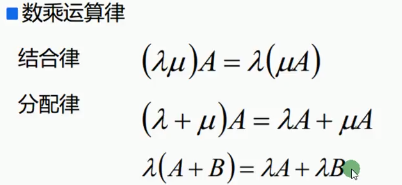
3、矩阵与向量的乘法：
前提：矩阵的列数等于向量的行数。
计算方式：左行 * 右列 对应元素乘积的和。
4、矩阵与矩阵的乘法：
得到的新矩阵由 左行右列 决定 行与列。即：（m*n）* (n*s) >>>> (m*s)
- 注意：矩阵与矩阵的乘法中没有交换律： AB != BA（A B 互逆除外 ）
- 当A逆矩阵存在时时：AC = AD >>>>> C = D 原因：并不是消去律，而是两边同时 乘上 A的逆矩阵化简。
5、矩阵的转置：
理解：对角线翻转。
转置的性质：
六、行列式基本知识：
1、行列式的特性：
理解：矩阵的一种运算方式。
①行列式一定是个方阵。
2、行列式的计算方法：
定义：所有不同行不同列的元素组合乘积的和。
（1）通过行列式的定义去计算：对角法则。
①逆序数的概念：t
（2）利用行列式的性质将行列式转化为上三角行列式：
转化时：从下到下，从左向右。
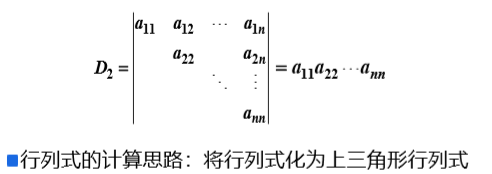
①行列式的性质 ：
性质一：
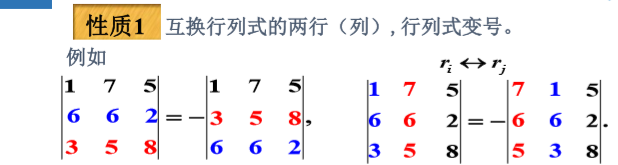
性质二：行列式的数乘（一定要区别于矩阵的数乘）
性质三：行列式如果某一行或某一列与另一行或者另一列存在倍数或者相同，行列式的数值为零。
性质四：行列式之间的加法：
前提：①两个行列式形状相同。
②两个行列式仅有一行或一列的元素不相同。
结果：相同元素覆盖照抄，不同的行的元素对应相加。
性质五：
（3）根据某行或者某列的代数余子式展开：
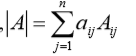
3、行列式余子式和代数余子式：
4、伴随矩阵：
表达式结论：
A 是一个 n阶 方阵。E 单位矩阵。该结果是一个对角矩阵，对角线的元素都是 | A | 的 值。
5、方阵的逆：只有方阵才有逆。
1、可逆矩阵的定义：
- 理解：可逆方阵 <<< >>> 可以初等变换为 E 即： AB = BA = E
- 可逆方阵 <<< >>> | A | != 0
2、方阵可逆的充要条件： 两个条件等价。
①
② 矩阵行列式的值 | A | ！= 0 。
3、可逆方阵的性质：
4、n阶方阵逆矩阵的计算：
第一种方法：
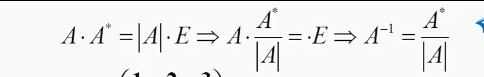
②第二种方法：
利用A 与 E 的增广矩阵 的初等变换 >>>>>>>>>>>>>>>>>>>>>.. 求解出 A的逆矩阵。
七、矩阵的初等变换：
- 注意：矩阵换行与行列式换行不同（行列式的换行值的符号会发生变化）
- 矩阵的 初等列变换 与 初等行变换 统称为初等变换。
- 可以通过 初等行变换 转化为 E 的方阵为可逆方阵，否则为奇异矩阵。
矩阵初等变换的理解：线性方程组加减消元。
1、增广矩阵：
记做： B = （A，b）
2、初等变换的性质：
2、矩阵初等变换的分类：
（1、普通的行阶梯矩阵：
（2、行最简形矩阵：
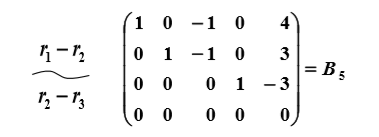
（3、标准形矩阵：
特性：
3、初等变换的定理：
其中： PA = B 是初等变化的 代数 表达形式。P是某个可逆方阵。
方阵可逆的充要条件：
4、初等变换的应用：
（1）利用初等行变换求解逆矩阵：
例：求解A 的逆矩阵：
思路：将A 与 E 创建 增广矩阵 B ， B= （A，E） >>>>> 通过初等行变换 >>>>>> (E，P） P 就是A的 可逆矩阵：P * A = E。
（2）利用初等行变换求解方程组的解：
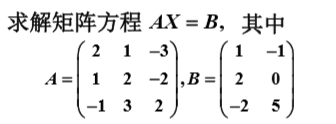
思路：类似上述求解逆矩阵的方法： 
解法：增广矩阵：
