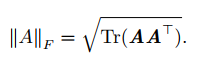1 标量、向量、矩阵和张量
2 矩阵和向量相乘
3 单位矩阵和逆矩阵
3.0 单位矩阵
a = np.identity(3) # 三行三列单位矩阵3.1 矩阵的逆
A = [[1.0,2.0],[3.0,4.0]]
A_inv = np.linalg.inv(A)
print("A 的逆矩阵", A_inv)3.1 转置
A = np.array([[1.0,2.0],[1.0,0.0],[2.0,3.0]])
A_t = A.transpose()
print("A:", A)
print("A 的转置:", A_t)3.2 矩阵相加
a = np.array([[1.0,2.0],[3.0,4.0]])
b = np.array([[6.0,7.0],[8.0,9.0]])
print("矩阵相加: ", a + b)3.3 矩阵乘法
m1 = np.array([[1.0,3.0],[1.0,0.0]])
m2 = np.array([[1.0,2.0],[5.0,0.0]])
print("按矩阵乘法规则: ", np.dot(m1, m2))
print("按逐元素相乘: ", np.multiply(m1, m2))
print("按逐元素相乘: ", m1*m2)
v1 = np.array([1.0,2.0])
v2 = np.array([4.0,5.0])
print("向量内积: ", np.dot(v1, v2))4 线性相关和生成子空间
5 范数
5.0 代码实现
5.0.1 向量的L1 L2 无穷范数
a = np.array([1.0,3.0])
print("向量 2 范数", np.linalg.norm(a,ord=2))
print("向量 1 范数", np.linalg.norm(a,ord=1))
print("向量无穷范数", np.linalg.norm(a,ord=np.inf))5.0.2 矩阵的F范数
a = np.array([[1.0,3.0],[2.0,1.0]])
print("矩阵 F 范数", np.linalg.norm(a,ord="fro"))5.1 范数的总定义
范数是将向量映射到非负值的函数。直观上来说,向量 x 的范数衡量从原点到点 x 的距离。
5.1.1 定义
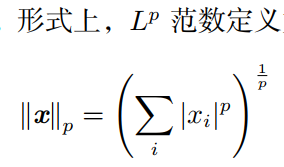
5.1 L1范数
5.1.1 定义
当机器学习问题中零和非零元素之间的差异非常重要时,在这些情况下,转而使用在各个位置斜率相同,通常会使用L1范数,也经常作为表示非零元素数目的替代函数。
5.1.2 数学表达
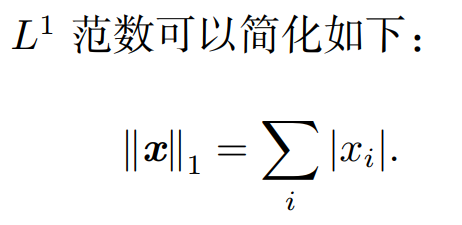
5.2 L2范数/欧几里得范数
表示从原点出发到向量 x 确定的点的欧几里得距离。
5.2.1 平方 L2 范数
也经常用来衡量向量的大小,可以简单地通过点积计算,在原点附近增长得十分缓慢。
5.2.2 平方L2范数与L2 范数对比
平方L2范数对x中每个元素的导数只取决于对应的元素。
L2范数对每个元素的导数却和整个向量相关。
5.3 最大范数
5.3.1 含义
表示向量中具有最大幅值的元素的绝对值:
5.3.2 定义
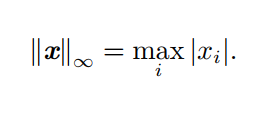
5.4 F范数
5.4.1 含义
F范数用来衡量矩阵的大小
5.4.2 数学定义
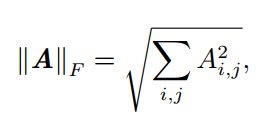
5.5 用范数表示点积

6 特殊矩阵
6.1 对角矩阵
只在主对角线上含有非零元素,其他位置都是零。
6.1.1 对角矩阵的含义
通过将一些矩阵限制为对角矩阵,我们可以得到计算代价较低的(并且简明扼要的)算法。
6.1.2 非标准对角矩阵的乘法计算

6.2 对称矩阵
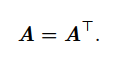
6.3 正交矩阵
行向量和列向量是分别标准正交的方阵:
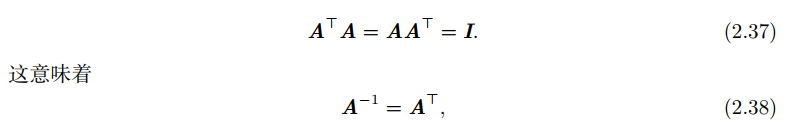
6.4 单位向量与正交

6.5 标准正交
如果这些向量不仅互相正交,并且范数都为1,那么我们称它们是标准正交。
7 特征分解
7.0 代码实现:特征分解
A = np.array([[1.0,2.0,3.0],
[4.0,5.0,6.0],
[7.0,8.0,9.0]])
# 计算特征值
print("特征值:", np.linalg.eigvals(A))
# 计算特征值和特征向量
eigvals,eigvectors = np.linalg.eig(A)
print("特征值:", eigvals)
print("特征向量:", eigvectors)7.1 定义
将矩阵分解成一组特征向量和特征值。
7.2 计算方法

7.3 Tip
不是每一个矩阵都可以分解成特征值和特征向量。
每个实对称矩阵都可以分解成实特征向量和实特征值。

7.4 正定、半正定、负定、半负定矩阵
- 所有特征值都是正数的矩阵被称为正定矩阵。
- 所有特征值都是非负数的矩阵被称为半正定矩阵。
- 所有特征值都是负数的矩阵被称为负定矩阵。
- 所有特征值都是非正数的矩阵被称为半负定矩阵。
8 奇异值分解(singular value decomposition, SVD)
8.0 代码实现奇异值分解
A = np.array([[1.0,2.0,3.0],
[4.0,5.0,6.0]])
U,D,V = np.linalg.svd(A)
print("U:", U)
print("D:", D)
print("V:", V)8.1 含义
将矩阵分解为奇异向量和奇异值。
8.1 分解计算方法

9 伪逆
9.1 解决的问题
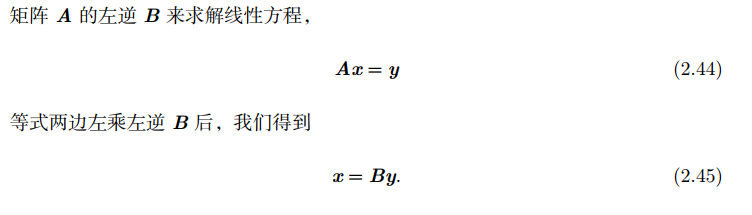
如果矩阵A的行数大于列数,那么上述方程可能没有解。如果矩阵A的行数小于列数,那么上述矩阵可能有多个解。
9.2 计算过程

10 迹运算
10.1 迹的定义

10.2 迹运算提供了描述矩阵Frobenius范数的方式:
10.3 运算规则
10.3.1 迹运算在转置运算下是不变的
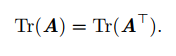
10.3.2 多个矩阵相乘得到的方阵的迹,和将这些矩阵中的最后一个挪到最前面之后相乘的迹是相同的。
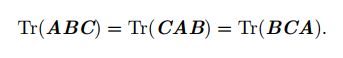
10.3.3 循环置换后矩阵乘积得到的矩阵形状变了,迹运算的结果依然不变。
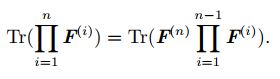
10.3.4 标量在迹运算后仍然是它自己
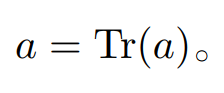
11 行列式
11.1 定义
行列式,记作det(A),是一个将方阵A映射到实数的函数。
11.2 行列式的特点
- 行列式等于矩阵特征值的乘积。
- 行列式的绝对值可以用来衡量矩阵参与矩阵乘法后空间扩大或者缩小多少。
- 如果行列式是0,那么空间至少沿着某一维完全收缩,使其失去所有的体积。
- 如果行列式是1,那么这个转换保持空间体积不变。