本文根据《A finite-time convergent dynamic system for solving online simultaneous linear equations》做的总结。
该文与基于梯度的动力系统和张动力系统做比较，提出了有限时间收敛动力系统，该系统可以在有限时间收敛，而前两者只能在无限时间收敛，可能减少在实时处理领域中的使用。
求解在线联立线性方程组广泛的在科学和工程领域遇到，因此，已经开发了许多用于联立线性方程的数值解的迭代算法。由与串行处理算法的时间复杂度为O（n^3），在大规模在线应用中可能不够高效。这是因为当应用于大规模在线应用问题的在线解决方案时，这些相关的迭代数值算法应该在每个采样周期内完成，并且当采样率太高而算法无法在单个采样周期内完成计算时算法失败。近些年来，由于动力学方法有高速度的并行处特点和潜在的硬件实施特点，在求解在线线性方程时被视为最佳选择。
联立线性方程式：
A(x)-b=0；
一、基于梯度动力系统：（无限时间）
1：定义一个基于平方的能量函数
,当且仅当联立线性方程的解x等于理论解x *时，才能实现其最小点。
2：沿着能量函数的负梯度下降方向演化，直到达到最小值。
设计参数γ> 0用于缩放收敛速度，上标T表示矩阵或向量的转置;
3：基于负梯度的学习规则导致基于梯度的动态系统为
，其中设计参数γ> 0用于调整基于梯度的动态系统的收敛率。 x（t），从初始状态x（0）∈R开始，表示对应于理论解x *的神经状态。
二、张动力系统（可用于解决在线时变问题和时不变问题）
与基于梯度动力系统不同，从基于梯度的动态系统来看，张动态系统通过定义无限的错误监控功能得到了好的引入。比梯度动力系统收敛性能好一些。
1：定义一个不定误差函数
；如果e(t)=0，理论解可以得到。
2：采用设计公式
，使得随着时间t的继续，e（t）收敛于零。
3：扩展设计公式，并考虑到
，我们可以得到这样一个隐式动力学模型，如
三、有限时间收敛动力学系统（增加一个特殊构造的激活函数）
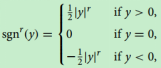
定理：给定非奇异系数矩阵A∈Rn×n和向量b∈Rn，我们的模型（3）的状态向量x（t）从任意随机生成的初始状态x（0）开始，有限时间收敛线性方程理论解。
其中e +（0）和e-（0）分别表示向量Ax（0）-b中的最大和最小元素。
证明：
为了便于说明，我们使用E（0）= Ax（0）-b代表误差函数E（t）的初始值。 将e +（t）定义为E（t）中具有最大初始值e +（0）= max {E（0）}的元素; 并且将e-（t）定义为E（t）中具有最小初始值e-（0）= min {E（0）}的元素。
因此e-（0）<=ei（t）<=e +（0）。这意味着当e +（t）和e-（t）都达到零时，对于所有可能的i，ei（t）收敛到零。 换句话说，我们的模型（3）的收敛时间受到动力学e +（t）和e-（t）之间的较大的时间所限制，即tc <= max {tc +，tc-}其中tc +和tc - 分别表示e +（t）和e-（t）的动态的收敛时间。
这表示在时间段|e+(0)|1−r/γ (1 − r)时L(t)收敛到零.
t > |e+(0)|1−r/γ (1 − r)时e+(t)是零，tc+ < |e+(0)|1−r/γ (1 − r)
t > |e−(0)|1−r/γ (1 − r)时e-(t)是零，tc− < |e−(0)|1−r/γ (1 − r)
所以得出结论：
这意味着我们的模型（3）的状态向量x（t），从任何随机生成的初始状态x（0）开始，收敛到有限时间tc的线性方程的理论解。 另外，理论上误差界限等于零。
收敛性能：基于梯度的动力系统 < 张动力系统 < 有限时间收敛动力系统。