举一个经典的例子,社会学家经常把人按其经济状况分成3类:下层、中层、上层,我们用1,2,3 分别代表这三个阶层。社会学家们发现决定一个人的收入阶层的最重要的因素就是其父母的收入阶层。如果一个人的收入属于下层类别,那么他的孩子属于下层收入的概率是 0.65, 属于中层收入的概率是 0.28, 属于上层收入的概率是 0.07。事实上,从父代到子代,收入阶层的变化的转移概率如下

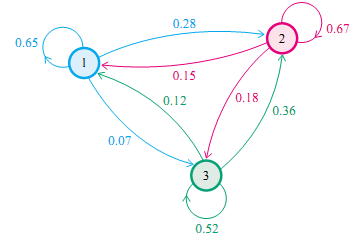
假设初始概率分布为[0.210, 0.680, 0.110],则我们可以计算前10代人的分布状况如下。
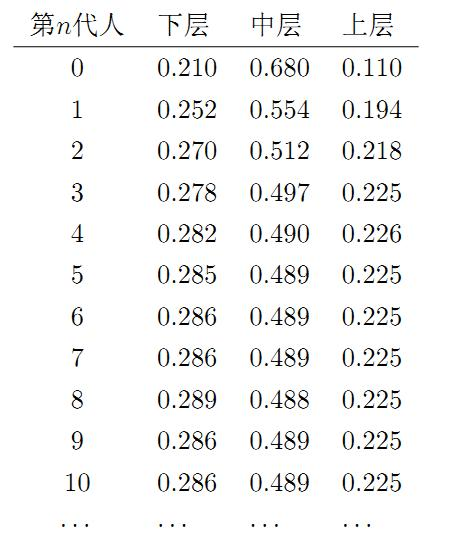
我们发现从第7代人开始,这个分布就稳定在[0.286, 0.489, 0.225],这个是偶然的吗?我们换一个初始概率分布[0.75, 0.15, 0.1],试试看,继续计算前代人的分布状况如下
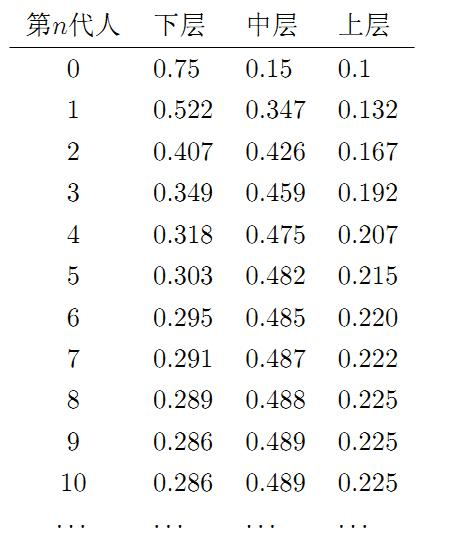
从第9代人开始,这个分布就稳定在[0.286, 0.489, 0.225]。不管从哪一个初始分布[0.210, 0.680, 0.110]或者[0.75, 0.15, 0.1]开始,转移多次后就能达到平稳不变的分布[0.286, 0.489, 0.225]。
因此,马尔科夫的稳定分布与初始分布无关,只与转移概率矩阵有关。
在转移概率矩阵P作用下达到的平稳分布$\pi(x)$,我们称之为马氏链平稳分布,有如下定理:

任意两个状态连通并非指状态i可以一步转移到j,而是指状态i可以通过有限的次数转移到j。

1. 状态转移矩阵自乘多次转移后,会得到一个稳定值
2. 马氏链稳定后,所有状态i转移到状态j的概率之和是稳定的
3. 一个状态转移矩阵只有唯一一个对应的稳定分布$\pi(x)$
细致平稳条件:
如果非周期马尔科夫链的状态转移矩阵P和概率分布$\pi(x)$对于所有的$i,j$满足:
则称概率分布$\pi(x)$是状态转移矩阵P的平稳分布。
证明:
$\begin{array}{l}
\sum\limits_{i = 0}^\infty {\pi (i)P(i,j)} = \sum\limits_{j = 0}^\infty {\pi (j)P(j,i)} \\
\pi (j) = \pi (j)\sum\limits_{j = 0}^\infty {P(j,i)}
\end{array}$
也就是
$\pi P = \pi $
需要注意的是这是一个充分条件,而不是必要条件,也就是说存在具有平稳分布的马尔科夫链不满足此细致平衡条件。