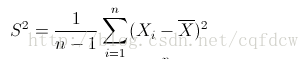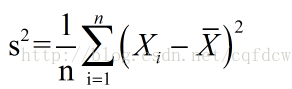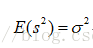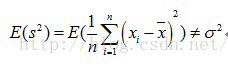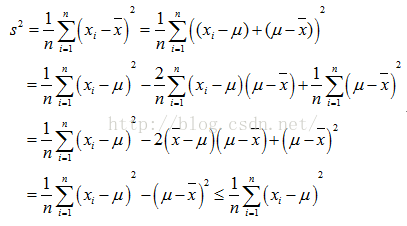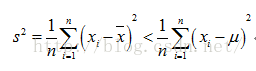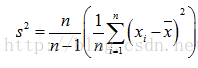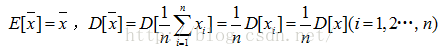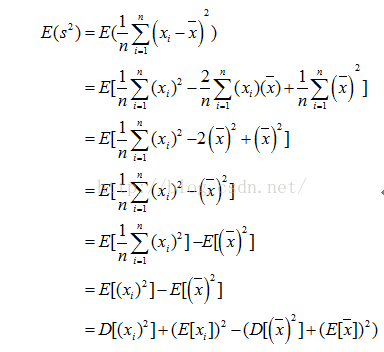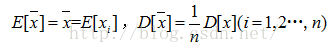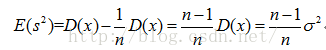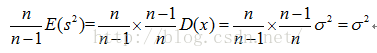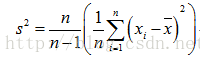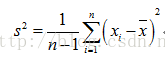一、方差(variance):衡量随机变量或一组数据时离散程度的度量。
概率论中方差用来度量随机变量和其数学期望(即均值)之间的偏离程度。
统计中的方差(样本方差)是每个样本值与全体样本值的平均数之差的平方值的平均数。
概率论中的方差表示方法 :
样本方差,无偏估计、无偏方差(unbiased variance)。对于一组随机变量,从中随机抽取N个 样本,这组样本的方差就 是Xi^2平方和除以N-1。
总体方差,也叫做有偏估计,其实就是我们从初高中就学到的那个标准定义的方差,除数是N。

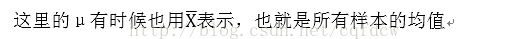
二、为什么样本方差的分母是n-1?为什么它又叫做无偏估计?
简单的回答,是因为因为均值你已经用了n个数的平均来做估计在求方差时,只有(n-1)个数和均值信息是不相关的。
而你的第n个数已经可以由前(n-1)个数和均值来唯一确定,实际上没有信息量。所以在计算方差时,只除以(n-1)。
那么更严格的证明呢?
样本方差计算公式里分母为n-1的目的是为了让方差的估计是无偏的。
无偏的估计(unbiased estimator)比有偏估计(biased estimator)更好是符合直觉的,尽管有的统计学家认为让mean square error即MSE最小才更有意义,这个问题我们不在这里探讨;
不符合直觉的是,为什么分母必须得是n-1而不是n才能使得该估计无偏。
首先,我们假定随机变量的数学期望是已知的,然而方差未知。在这个条件下,根据方差的定义我们有
由此可得
是方差
的一个无偏估计,注意式中的分母不偏不倚正好是
!
这个结果符合直觉,并且在数学上也是显而易见的。
现在,我们考虑随机变量的数学期望
是未知的情形。这时,我们会倾向于无脑直接用样本均值
替换掉上面式子中的
。这样做有什么后果呢?后果就是,
如果直接使用作为估计,那么你会倾向于低估方差!
这是因为:
换言之,除非正好,否则我们一定有
,
而不等式右边的那位才是的对方差的“正确”估计!
这个不等式说明了,为什么直接使用会导致对方差的低估。
那么,在不知道随机变量真实数学期望的前提下,如何“正确”的估计方差呢?答案是把上式中的分母换成
,通过这种方法把原来的偏小的估计“放大”一点点,我们就能获得对方差的正确估计了:
三、理论推导
为了方便叙述,在这里说明好数学符号:
前面说过样本方差之所以要除以(n-1)是因为这样的方差估计量才是关于总体方差的无偏估计量。在公式上来讲的话就是样本方差的估计量的期望要等于总体方差。如下:
但是没有修正的方差公式,它的期望是不等于总体方差的
也就是说,样本方差估计量如果是用没有修正的方差公式来估计总计方差的话是有偏差的
下面给出比较好理解的公式推导过程:
也就是说,除非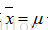
需要注意的是不等式右边的才是的对方差的“正确”估计,但是我们是不知道真正的总体均值是多少的,只能通过样本的均值来代替总体的均值。
所以样本方差估计量如果是用没有修正的方差公式来估计总计方差的话是会有偏差,是会低估了总体的样本方差的。为了能无偏差的估计总体方差,所以要对方差计算公式进行修正,修正公式如下:
这种修正后的估计量将是总体方差的无偏估计量,下面将会给出这种修正的一个来源;
为了能搞懂这种修正是怎么来的,首先我们得有下面几个等式:
1.方差计算公式:
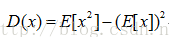
2. 均值的均值、方差计算公式:
对于没有修正的方差计算公式我们有:
因为:
所以有:
在这里如果想修正的方差公式,让修正后的方差公式求出的方差的期望为总体方差的话就需要在没有修正的方差公式前面加上来进行修正,即:
所以就会有这样的修正公式:
而我们看到的都是修正后的最终结果:
这就解释了为什么要对方差计算公式进行修正,且为什么要这样修正。
上面的解释如果有什么错误,或者有哪些解释不正确的地方欢迎大家指正。谢谢大家。希望能对大家有点帮助。
参考:
https://blog.csdn.net/zxyhhjs2017/article/details/79149111
https://blog.csdn.net/qq_39521554/article/details/79633207
https://blog.csdn.net/cqfdcw/article/details/78173839