总体样本方差的无偏估计样本方差为什么除以n-1

本文链接： https://blog.csdn.net/qq_16587307/article/details/81328773

我们先从最基本的一些概念入手。

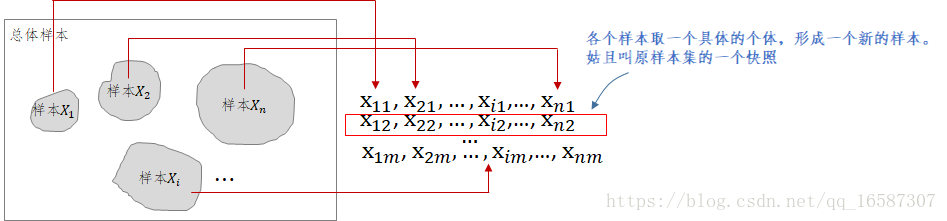
如下图，脑子里要浮现出总体样本 $X$ ，还有一系列随机选取的样本 $X_{1},X_{2},...,X_{n}$ 。只要是样本，脑子里就要浮现出它的集合属性，它不是单个个体，而是一堆随机个体集合。样本 $X_{i}$ 是总体样本中随机抽取一系列个体组成的集合，它是总体样本的一部分。

应该把样本 $X_{i}$ 和总体样本 $X$ 一样进行抽象化理解，因此样本 $X_{i}$ 也存在期望 $E(X_{i})$ 和方差 $D(X_{i})$ 。

这里有一个重要的假设，就是随机选取的样本 $X_{i}$ 与总体样本同分布，它的意思就是说他们的统计特性是完全一样的，即他们的期望值一样，他们的方差值也是一样的：

$E(X_{i})=E(X)=\mu$

$D(X_{i})=D(X)=\sigma ^{2}$

另外，由于每个样本的选取是随机的，因此可以假设 $X_{1},X_{2},...,X_{n}$ 不相关(意味着协方差为0，即 $Cov(X_{i},X{j})=0,i\neq j$ )，根据方差性质就有:

$D(X_{i}+X_{j})=D(X_{i})+D(X_{j})+2Cov(X_{i},X_{j})=D(X_{i})+D(X_{j})=2\sigma ^{2}$

另外，还需要知道方差另外一个性质：

$D(aX_{i})=a^{2}D(X_{i}),a$ 为常数。

还有一个，别忘了方差的基本公式：

$D(X)=E(X^2)-E^2(X)$

以上的公式都很容易百度得到，也非常容易理解。这里不赘述。

2）无偏估计

接下来，我们来理解下什么叫无偏估计。

定义：设统计量 $\hat{\Theta}=\hat{\Theta}(X_{1},X_{2},...,X_{n})$ 是总体中未知参数 $\Theta$ 的估计量，若 $E(\hat{\Theta })=\Theta$ ，则称 $\hat{\Theta }$ 为 $\Theta$ 的无偏估计量；否则称为有偏估计量。

上面这个定义的意思就是说如果你拿到了一堆样本观测值，然后想通过这一堆观测值去估计某个统计量 $\Theta$ ，一般就是想估计总体的期望或方差，如果你选择的方法所估计出来的统计量 $\hat{\Theta}$ 的期望值与总体样本的统计量 $\Theta$ 相等，那么我们称这种方法下的估计量是无偏估计，否则，就称这种方法下的估计量为有偏估计量。

按照这么理解，那么有偏无偏是针对你选择估计的方法所说的，它并不是针对具体某一次估计出来的估计量结果。如果方法不对，即使你恰好在某一次计算出来一个值和总体样本统计量值相同，也并不代表你选的这个方法是无偏的。为什么呢？这是因为单次 $\hat{\Theta}$ 值是和你选取的样本相关的，每次样本（更加严格的意义是某次样本快照）的值变化了，那么每次 $\hat{\Theta}$ 的值就有可能跟着变化，你就需对这么多 $\hat{\Theta}$ 求期望值来判断 $\hat{\Theta}$ 的可信程度，如果一直重复这个试验，然后它的期望值与总体样本的统计量 $\Theta$ 一样，那么称按照这种方法估计出来的统计量是无偏的。

来一点题外话：

但凡是想通过有限的信息去"估计"一个整体的"量"，这种情形下谈这个"估计"的方法“有偏”\“无偏”才有意义。一般来说，这种情形下，这个被估计的"量"肯定是有碍于技术或者现实情况无法严格准确获取，比如因为成本过高这些"量"无法通过穷举或者其他办法获知。否则，如果被估计的"量"很容易获取，就不需要"估计"了，采用统计方法就可以了。

如果你只是要进行简单的"统计"就能获得你想要的"量"，那么没必要去关心所采用的方法是"有偏"还是“无偏"；尤其是当整体信息很容易获取的情况下谈"有偏"还是“无偏"就毫无意义。比如要谈某个班级的身高的平均值，直接将身高总数除以班级人数就可以了，因为根本没必要去"估计"，因为它仅仅是个"统计"问题；同样的，求一个班级的身高方差也不用任何纠结，求方差过程中除以班级人数就OK了，没有必要非常变态的研究是除以"班级总人数"还是"班级总人数-1"，你要是去纠结这个，那就是吃饱了撑的了。但是，假如学校有几万人，你要统计的是整个学校所有的人的平均身高，这个时候一个一个进行统计是不现实的，反而需要使用的"估计"的方法。你采用的方法是随便抓100个人过来，将这100人总的身高数值除以100，估计出来的平均值就可以假设认为是整个学校的身高平均值，因为，你是用部分样本估计了总体样本的一个”量“，所以这个是"估计"；此时，要是估计整个学校学生身高的方差，如果要想估计方法"无偏", 那就不是除以100了，而是除以99。当然，如果你是一位粗人，无所谓啥"有偏"还是“无偏"的束缚，那么你直接除以100也不会遭到嘲笑的，具体原因得继续往下看。总之，无法通过整体直接"统计"获得你想要的"量"时，你只能通过"部分样本"来做"整体样本""量"的估计时，谈估计方法的"有偏"还是"无偏"才是有意义的。

3）样本均值的无偏估计

接下来探讨一下下面的结论：

定理1：样本均值 $\bar{X}$ 是总体样本均值 $\mu$ 的无偏估计。

注意：这里样本均值 $\bar{X}$ 不是指某个样本 $X_{i}$ 的均值。

这里需要看上面这张图，这里的均指的是特定某次样本集合 $(X_{1},X_{2},...,X_{n})$ 的快照（上图红色框）,显然这个快照也是一个样本，只不过这个样本它的样本大小固定为n，这与抽象的样本不一样（一般我们想象抽象的样本，比如 $X_{i}$ ，是无限大的）。

明显，

第一个样本(快照)均值是长这样子的： $\frac{1}{n}(x_{11}+x_{21}+...+x_{i1}+...+x_{n1})=\hat{\mu _{1}}$

第二个样本(快照)均值是长这样子的： $\frac{1}{n}(x_{12}+x_{22}+...+x_{i2}+...+x_{n2})=\hat{\mu _{2}}$

....依此类推...

$x_{ij}$ 表示第 $j$ 次随机从从本 $X_{i}$ 获取一个个体。

试验一直进行下去，你就会有一些列估计出来的样本(快照)均值 $\hat{\mu _{1}},\hat{\mu _{2}}...\hat{\mu _{i}},\hat{\mu _{m}}...$ ，实际上这也称为了一个样本，我们称为均值的样本，既然是样本，它就也有统计量。我们这里重点关注这个均值样本的期望。因为按照估计量的有偏无偏定义，如果 $E(\hat{\mu})=\mu$ ，那么按照这个方法估计的均值 $\hat{\mu }$ 就是无偏的。仔细思考，估计量有偏无偏它是针对你所选定的某个估计方法所形成的估计量样本空间来讨论的，讨论单次试验形成的估计量是没有太大意义的，只有针对形成的估计量样本空间才有意义。

下面验证上面的方法形成的 $\hat{\mu}$ 估计是无偏的。

$E(\hat{\mu})=\frac{1}{m}(\hat{\mu}_{1}+\hat{\mu}_{2}+...+\hat{\mu}_{m})$

$=\frac{1}{n}(\frac{x_{11}+x_{12}+...+x_{1m}}{m}+\frac{x_{21}+x_{22}+...+x_{2m}}{m}+...+\frac{x_{n1}+x_{n2}+...+x_{nm}}{m})$

$=\frac{1}{n}(E(X_{1})+E(X_{2})+...+E(X_{n}))$

$=\frac{1}{n}(n*\mu )$

$=\mu$

这么一来，就和教科书和网上的资料结果上都对上了，教科书上的公式在下面列出（ $\hat{\mu}$ 符号用 $\bar{X}$ 代替）：

$E(\bar{X})=E(\frac{1}{n}\sum_{i=1}^{n}X_{i} )=\frac{1}{n}\sum_{i=1}^{n}E(X_{i})=\mu$

有了前面的分析，上面的教科书公式就很好理解了，注意，里头的 $X_{i}$ 是原始样本， $\bar{X}$ 也是样本!!! 公式推导过程中， $\bar{X}=\frac{1}{n}\sum_{i=1}^{n}X_{i}$ 表示了原始的 $(X_{1},X_{2},...,X_{n})$ 样本快照求和后再除以n形成的估计量样本，所以是可以对其再进行求期望的。

讨论完估计量样本 $\bar{X}$ 的均值，我们别忘了，既然它是个样本，那么可以计算 $\bar{X}$ 的方差 $D(\bar X)$ （后面会用到）:

$D(\bar X)=D(\frac{1}{n}\sum_{i=1}^{n}X_{i})$

$=\frac{1}{n^2}D(\sum_{i=1}^{n}X_{i})$

$=\frac{n\sigma ^2}{n^2}=\frac{\sigma ^2}{n}$

所以，样本（快照）均值的期望还是总体期望，但是，样本（快照)均值的方差却不是原来的方差了，它变成原来方差的1/n。这也容易理解，方差变小了是由于样本不是原来的样本 $X_{i}$ 了，现在的样本是均值化后的新样本 $\bar {X}$ ，既然均值化了，那么比起原来的老样本 $X_{i}$ ，它的离散程度显然是应当变小的。

4）样本方差的无偏估计

定理2：样本方差 $S^{2}=\frac{1}{n-1}\sum_{i=1}^{n}(X_{i}-\bar{X})^{2}$ 是总体样本方差 $\sigma ^{2}$ 的无偏估计。

也就是需要证明下面的结论：

$E(S^2)=E(\frac{1}{n-1}\sum_{i=1}^{n}(X_{i}-\bar{X})^2)=\sigma ^2$

首先，脑子里要非常清楚，你截至目前，仅仅知道以下内容：

$E(X_{i})=E(X)=\mu$

$D(X_{i})=D(X)=\sigma ^{2}$

$Cov(X_{i}X{j})=0,i\neq j$

$D(X_{i}+X_{j})=D(X_{i})+D(X_{j})=2\sigma ^{2},i\neq j$

$D(X)=\sigma ^{2}=E(X^2)-E(X)^2=E(X^2)-\mu^2$

${\color{Red} E(\bar{X})=\mu}$

${\color{Red} D(\bar X)=\frac{\sigma ^2}{n}}$

其中前面5个来自1），最后2个来自3)。

至于为什么是 $S^{2}=\frac{1}{n-1}\sum_{i=1}^{n}(X_{i}-\bar{X})^{2}$ ，而不是 $S^{2}=\frac{1}{n}\sum_{n}^{i=1}(X_{i}-\bar{X})^{2}$ ，需要看下面的证明。

$E(S^{2})=E(\frac{1}{n-1}\sum_{i=1}^{n}(X_{i}-\bar{X})^{2})=\frac{1}{n-1}E(\sum_{i=1}^{n}X_{i}^2-n \bar{X}^{2})$

$=\frac{1}{n-1}(\sum_{i=1}^{n}E(X_{i}^2)-nE(\bar{X}^{2}) )$

$=\frac{1}{n-1}(\sum_{i=1}^{n}[D(X_{i})+E^2(X_{i})]-n[D(\bar{X})+E^{2}(\bar{X}) ])$

$=\frac{1}{n-1}(\sum_{i=1}^{n}[\sigma ^2+\mu^2]-n[\frac{1}{n}\sigma ^2+\mu^{2} ])=\sigma ^2$

那么为什么会导致这么个奇怪的结果，不是 $\frac{1}{n}$ 而是 $\frac{1}{n-1}$ ？

仔细看上面的公式，如果 $D(\bar X)=0$ ，那么就应该是 $\frac{1}{n}$ 了，但是残酷的事实是 $D(\bar X)\neq 0$ （除非 $\sigma$ 本身就等于0），导致 $\frac{1}{n-1}$ 的罪魁祸首是 $D(\bar X)\neq 0$ 。这就有告诉我们， $D(\bar X)$ 虽然将方差缩小了n倍，但是仍然还有残存，除非 $\sigma$ 本身就等于0，才会有 $D(\bar X)=0$ ，但这就意味着所有样本的个体处处等于 $\mu$ 。

还有一种情况，如果你事先就知道 $\mu$ ，那么 $S^{2}=\frac{1}{n}\sum_{i=1}^{n}(X_{i}-\mu)^{2}$ 就是 $\sigma ^{2}$ 的无偏估计，这个时候就是 $\frac{1}{n}$ 了。

---------------------------------------------------------------------------------------------------------------------------------------------

有人还是问我为什么 $\mu$ （总体均值）已知，就可以用 $S^{2}=\frac{1}{n}\sum_{i=1}^{n}(X_{i}-\mu)^{2}$ 作为总体方差 $\sigma ^{2}$ 的无偏估计，这个完全直接推导就可以证明。证明如下：

$E(S^{2})=E(\frac{1}{n}\sum_{i=1}^{n}(X_{i}-\mu)^{2})$

$=\frac{1}{n}\sum_{i=1}^{n}E[(X_{i}-\mu)^{2}]$

$=\frac{1}{n}\sum_{i=1}^{n}[E(X_{i}^2)-2\mu E(X_{i})+\mu^{2}]$

$=\frac{1}{n}\sum_{i=1}^{n}[E(X_{i}^2)-\mu^{2}]$

$=\frac{1}{n}\sum_{i=1}^{n}[\sigma^2+\mu^2-\mu^{2}]$

$=\sigma^{2}$

这个结论告诉我们，如果某个人很牛逼，他可以知道确切的总体样本均值 $\mu$ ，那么就可以用 $S^{2}=\frac{1}{n}\sum_{i=1}^{n}(X_{i}-\mu)^{2}$ 来估计总体样本方差 $\sigma^{2}$ ，并且这个估计方法是保证你无偏的。

而上面的 $S^{2}=\frac{1}{n-1}\sum_{i=1}^{n}(X_{i}-\bar{X})^{2}$ ，请睁大眼睛看清楚，用的是 $\bar{X}$ 。大部分的实际应用情况下，谁也不知道总体样本均值 $\mu$ (请问你知道全球人均身高么？鬼知道，地球上没有一个人可以知道！我想即使是外星爸爸也不知道！)，但是我还是想在全球人都不知道的情况下去估计总体的身高方差，怎么办？现在有个办法，我们可以去抓一些人（部分样本）来做一个部分样本均值，那就用部分样本均值也就是 $\bar{X}$ 来近似代表 $\mu$ （上面的定理1告诉我们这种方法对于估计 $\mu$ 是无偏的），但是现在我想估计另外一个东东，那个东东叫总体样本方差 $\sigma^{2}$ 。好了，我们可以也用 $\bar{X}$ 代入 $S^{2}=\frac{1}{n-1}\sum_{i=1}^{n}(X_{i}-\bar{X})^{2}$ 来估计总体样本方差 $\sigma^{2}$ ，并且如前面所分析的，这个估计方法针对 $\sigma^{2}$ 是无偏的。（至于为啥是奇怪的 $\frac{1}{n-1}$ ，简单直接的原因是因为我不知道总体样本均值 $\mu$ ，因为如果你能够知道 $\mu$ ，我们就可以不需要用奇怪的 $\frac{1}{n-1}$ ，我们就可以用 $S^{2}=\frac{1}{n}\sum_{i=1}^{n}(X_{i}-\mu)^{2}$ 去估计总体样本方差）。

总之， $S^{2}=\frac{1}{n}\sum_{i=1}^{n}(X_{i}-\mu)^{2}$ 是理论上的总体样本方差。 $S^{2}=\frac{1}{n-1}\sum_{i=1}^{n}(X_{i}-\bar{X})^{2}$ 是实际应用中采用的总体样本方差估计。

------------------------------------------------------------------------------------------------------------------------------------------------------------------

统计学中还有一个"自由度"的概念。为什么是除以n-1还可以从自由度角度进行解释，具体可以参看下面百度的解释：

自由度（统计学的自由度）

站内首发文章

ALTLI

发布了36 篇原创文章 · 获赞 20 · 访问量 2829

私信关注

本文链接： https://blog.csdn.net/qq_16587307/article/details/81328773